_广东省深圳实验学校2022-2023学年八年级上学期期中水平测试数学试卷 (含答案)

这是一份_广东省深圳实验学校2022-2023学年八年级上学期期中水平测试数学试卷 (含答案)，共22页。
2022-2023学年广东省深圳实验学校期中水平测试练习试卷
八年级数学
一.选择题（共10小题，每题3分，共30分）
1．（3分）在实数，0，，503，π，0.101中，无理数的个数是（　　）
A．2 B．3 C．4 D．5
2．（3分）在平面直角坐标系中，点P（﹣5，0）在（　　）
A．第二象限 B．第四象限 C．x轴上 D．y轴上
3．（3分）对于直线y＝﹣x﹣1的描述正确的是（　　）
A．y随x的增大而增大 B．与y轴的交点是（0，﹣1）
C．经过点（﹣2，﹣2） D．图象不经过第二象限
4．（3分）某班抽取6名同学参加体能测试，成绩如下：80，90，75，75，80，80．下列表述错误的是（　　）
A．众数是80 B．中位数是75 C．平均数是80 D．极差是15
5．（3分）在平面直角坐标系中，将函数y＝3x+2的图象向下平移3个单位长度，所得的函数的解析式是（　　）
A．y＝3x+5 B．y＝3x﹣5 C．y＝3x+1 D．y＝3x﹣1
6．（3分）下列计算中，正确的是（　　）
A． B．
C． D．
7．（3分）已知方程组和有相同的解，则a﹣2b的值为（　　）
A．9 B．10 C．11 D．12
8．（3分）下列图形中，表示一次函数y＝mx+n与正比例函数y＝mnx（m，n为常数，且mn≠0）的图象的是（　　）
A． B．
C． D．
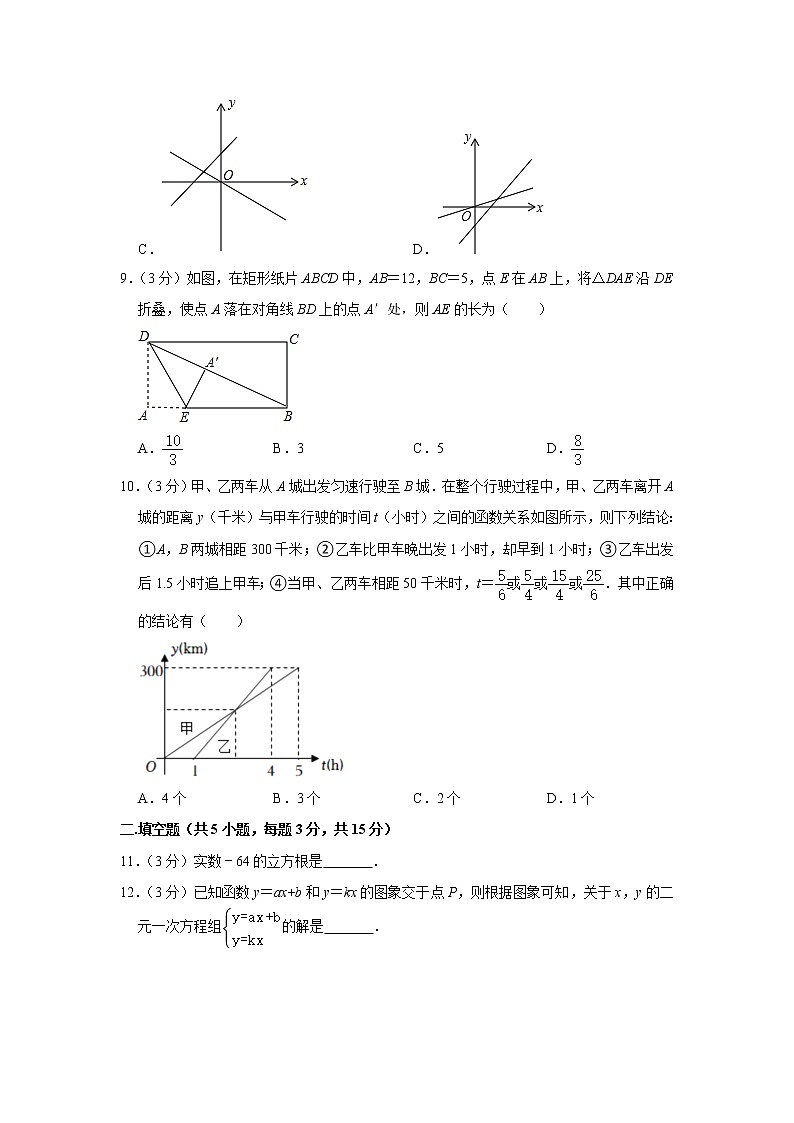
9．（3分）如图，在矩形纸片ABCD中，AB＝12，BC＝5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A′处，则AE的长为（　　）

A． B．3 C．5 D．
10．（3分）甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示，则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1小时；③乙车出发后1.5小时追上甲车；④当甲、乙两车相距50千米时，t＝或或或．其中正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
二.填空题（共5小题，每题3分，共15分）
11．（3分）实数﹣64的立方根是　 　．
12．（3分）已知函数y＝ax+b和y＝kx的图象交于点P，则根据图象可知，关于x，y的二元一次方程组的解是　 　．

13．（3分）如图，FD∥BE，则∠1+∠2﹣∠A＝　 　．

14．（3分）如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x、y轴的正半轴上，OA＝3，OB＝4，D为OB边的中点，E是OA边上的一个动点，当△CDE的周长最小时，E点坐标为　 　．

15．（3分）如图所示，A（﹣，0）、B（0，1）分别为x轴、y轴上的点，△ABC为等边三角形，点P（3，a）在第一象限内，且满足2S△ABP＝S△ABC，则a的值　 　．

三.解答题（共6题，共55分）
16．（8分）计算下列各式：
（1）；
（2）．
17．（8分）解方程：
（1）；
（2）．
18．（5分）如图，在直角坐标系内，已知点A（﹣1，0）．
（1）图中点B的坐标是 　 　；
（2）点B关于原点对称的点D的坐标是 　 　；点A关于y轴对称的点C的坐标是 　 　；
（3）在y轴上找一点F，使S△ACF＝S△ABC．那么点F的坐标为 　 　．

19．（6分）大家知道，是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，而，于是可用来表示的小数部分．请解答下列问题：
（1）的整数部分是 　 　，小数部分是 　 　；
（2）如果的整数部分为a，的小数部分为b，求的值．
20．（7分）某中学计划举行以“奋斗百年路，启航新征程”为主题的知识竞赛，并对获奖的同学给予奖励．现要购买甲、乙两种奖品，已知1件甲种奖品和2件乙种奖品共需40元，2件甲种奖品和3件乙种奖品共需70元．
（1）求甲、乙两种奖品的单价；
（2）根据颁奖计划，该中学需甲、乙两种奖品共60件，且甲种奖品不少于20件，应如何购买才能使总费用最少？并求出最少费用．
21．（8分）我们新定义一种三角形：两边平方和等于第三边平方的4倍的三角形叫做常态三角形．例如：某三角形三边长分别是5，6和8，因为62+82＝4×52＝100，所以这个三角形是常态三角形．
（1）若△ABC三边长分别是2，和4，则此三角形 　 　常态三角形（填“是”或“不是”）；
（2）若Rt△ABC是常态三角形，则此三角形的三边长之比为 　 　；
（3）如图，Rt△ABC中，∠ACB＝90°，BC＝6，D在AB上，且AD＝BD＝CD，若△BCD是常态三角形，求线段AC的长．

22．（8分）如图，直线y＝2x+m（m＞0）与x轴交于点A（﹣2，0），直线y＝﹣x+n（n＞0）与x轴、y轴分别交于B、C两点，并与直线y＝2x+m（m＞0）相交于点D，若AB＝4．
（1）求直线BC的解析式；
（2）求出四边形AOCD的面积；
（3）若E为x轴上一点，且△ACE为等腰三角形，请直接写出点E的坐标．

2022-2023学年广东省深圳实验学校期中水平测试练习试卷
八年级数学
（参考答案与解析）
一.选择题（共10小题，每题3分，共30分）
1．（3分）在实数，0，，503，π，0.101中，无理数的个数是（　　）
A．2 B．3 C．4 D．5
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
【解答】解：是分数，属于有理数；
0，503是整数，属于有理数；
0.101是有限小数，属于有理数；
无理数有：，π，共2个．
故选：A．
2．（3分）在平面直角坐标系中，点P（﹣5，0）在（　　）
A．第二象限 B．第四象限 C．x轴上 D．y轴上
【分析】根据点的坐标特点判断即可．
【解答】解：在平面直角坐标系中，点P（﹣5，0）在x轴上，
故选：C．
3．（3分）对于直线y＝﹣x﹣1的描述正确的是（　　）
A．y随x的增大而增大 B．与y轴的交点是（0，﹣1）
C．经过点（﹣2，﹣2） D．图象不经过第二象限
【分析】A．由k＝﹣＜0，利用一次函数的性质可得出y随x的增大而减小；B．利用一次函数图象上点的坐标特征可得出直线y＝﹣x﹣1与y轴的交点是（0，﹣1）；C．利用一次函数图象上点的坐标特征可得出直线y＝﹣x﹣1经过点（﹣2，0）；D．由k＝﹣＜0，b＝﹣1＜0，利用一次函数图象与系数的关系可得出直线y＝﹣x﹣1经过第二、三、四象限．
【解答】解：A．∵k＝﹣＜0，
∴y随x的增大而减小，选项A不符合题意；
B．当x＝0时，y＝﹣×0﹣1＝﹣1，
∴直线y＝﹣x﹣1与y轴的交点是（0，﹣1），选项B符合题意；
C．当x＝﹣2时，y＝﹣×（﹣2）﹣1＝0，
∴直线y＝﹣x﹣1经过点（﹣2，0），选项C不符合题意；
D．∵k＝﹣＜0，b＝﹣1＜0，
∴直线y＝﹣x﹣1经过第二、三、四象限，选项D不符合题意．
故选：B．
4．（3分）某班抽取6名同学参加体能测试，成绩如下：80，90，75，75，80，80．下列表述错误的是（　　）
A．众数是80 B．中位数是75 C．平均数是80 D．极差是15
【分析】根据平均数，中位数，众数，极差的概念逐项分析．
【解答】解：A、80出现的次数最多，所以众数是80，A正确；
B、把数据按大小排列，中间两个数为80，80，所以中位数是80，B错误；
C、平均数是＝80，C正确；
D、极差是90﹣75＝15，D正确．
故选：B．
5．（3分）在平面直角坐标系中，将函数y＝3x+2的图象向下平移3个单位长度，所得的函数的解析式是（　　）
A．y＝3x+5 B．y＝3x﹣5 C．y＝3x+1 D．y＝3x﹣1
【分析】根据解析式“上加下减”的平移规律解答即可．
【解答】解：将函数y＝3x+2的图象向下平移3个单位长度后，所得图象的函数关系式为y＝3x+2﹣3＝3x﹣1，
故选：D．
6．（3分）下列计算中，正确的是（　　）
A． B．
C． D．
【分析】先化简二次根式，再计算减法即可判断A；利用平方差公式和二次根式的性质计算可判断B；先化简二次根式，再计算减法即可判断C；分母有理化，再约分即可判断D．
【解答】解：A．﹣＝3﹣2＝1，此选项错误；
B．（2﹣）（2+）＝22﹣（）2＝4﹣5＝﹣1，此选项错误；
C．﹣＝2﹣＝，此选项计算正确；
D．＝＝3﹣1，此选项计算错误．
故选：C．
7．（3分）已知方程组和有相同的解，则a﹣2b的值为（　　）
A．9 B．10 C．11 D．12
【分析】根据同解方程组，把x+y＝﹣1和x﹣y＝3联立求出x、y，再代入其他两个方程即可解出a、b，进而求出结果．
【解答】解：由题意，联立方程组得：，
解得：，
将代入含a，b的两个方程，可得，
解得，
∴a﹣2b＝14﹣2×2＝14﹣4＝10．
故选：B．
8．（3分）下列图形中，表示一次函数y＝mx+n与正比例函数y＝mnx（m，n为常数，且mn≠0）的图象的是（　　）
A． B．
C． D．
【分析】根据“两数相乘，同号得正，异号得负”分两种情况讨论mn的符号，然后根据m、n同正时，同负时，一正一负或一负一正时，利用一次函数的性质进行判断．
【解答】解：①当mn＞0，m，n同号，同正时y＝mx+n过一，三，二象限，同负时过二，四，三象限；
②当mn＜0时，m，n异号，则y＝mx+n过一，四，四象限或二，四，一象限．
故选：A．
9．（3分）如图，在矩形纸片ABCD中，AB＝12，BC＝5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A′处，则AE的长为（　　）

A． B．3 C．5 D．
【分析】首先利用勾股定理计算出BD的长，再根据折叠可得AD＝A′D＝5，进而得到A′B的长，再设AE＝x，则A′E＝x，BE＝12﹣x，再在Rt△A′EB中利用勾股定理可得方程：（12﹣x）2＝x2+82，解出x的值，可得答案．
【解答】解：∵AB＝12，BC＝5，
∴AD＝5，
∴BD＝＝13，
根据折叠可得：AD＝A′D＝5，
∴A′B＝13﹣5＝8，
设AE＝x，则A′E＝x，BE＝12﹣x，
在Rt△A′EB中：（12﹣x）2＝x2+82，
解得：x＝．
故选：A．
10．（3分）甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示，则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1小时；③乙车出发后1.5小时追上甲车；④当甲、乙两车相距50千米时，t＝或或或．其中正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
【分析】观察图象可判断①②，由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式，可求得两函数图象的交点，可判断③，再令两函数解析式的差为50，可求得t，可判断④，可得出答案．
【解答】解：由图象可知A、B两城市之间的距离为300km，甲行驶的时间为5小时，而乙是在甲出发1小时后出发的，且用时3小时，即比甲早到1小时，
∴①②都正确；
设甲车离开A城的距离y与t的关系式为y甲＝kt，
把（5，300）代入可求得k＝60，
∴y甲＝60t，
设乙车离开A城的距离y与t的关系式为y乙＝mt+n，
把（1，0）和（4，300）代入可得，
解得，
∴y乙＝100t﹣100，
令y甲＝y乙可得：60t＝100t﹣100，
解得t＝2.5，
即甲、乙两直线的交点横坐标为t＝2.5，
此时乙出发时间为1.5小时，即乙车出发1.5小时后追上甲车，
∴③正确；
令|y甲﹣y乙|＝50，可得|60t﹣100t+100|＝50，即|100﹣40t|＝50，
当100﹣40t＝50时，可解得t＝，
当100﹣40t＝﹣50时，可解得t＝，
又当t＝时，y甲＝50，此时乙还没出发，
当t＝时，乙到达B城，y甲＝250；
综上可知当t的值为或或或时，两车相距50千米，
∴④正确；
综上可知正确的有①②③④共四个，
故选：A．
二.填空题（共5小题，每题3分，共15分）
11．（3分）实数﹣64的立方根是　﹣4　．
【分析】原式利用立方根定义计算即可得到结果．
【解答】解：∵（﹣4）3＝﹣64，
∴﹣64的立方根为﹣4，
故答案为：﹣4
12．（3分）已知函数y＝ax+b和y＝kx的图象交于点P，则根据图象可知，关于x，y的二元一次方程组的解是　　．

【分析】根据两图象的交点坐标，即可求出两函数的解析式组成的方程组的解．
【解答】解：根据图象可知：函数y＝ax+b和y＝kx的图象的交点P的坐标是（﹣3，﹣2），
∴方程组的解是．
故答案为：．
13．（3分）如图，FD∥BE，则∠1+∠2﹣∠A＝　180°　．

【分析】本题利用平行线的性质以及三角形内角和外角的关系解答
【解答】解：∵FD∥BE，∴∠2＝∠A+（180°﹣∠1），∠1＝∠A+（180°﹣∠2），
∴∠1+∠2＝2∠A+（180°﹣∠1）+（180°﹣∠2），
∴∠1+∠2﹣∠A＝180°．
故答案为：180°．
14．（3分）如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x、y轴的正半轴上，OA＝3，OB＝4，D为OB边的中点，E是OA边上的一个动点，当△CDE的周长最小时，E点坐标为　（1，0）　．

【分析】作出D的对称点D′连接CD′，将三角形的周长转化为CE+CD，根据两点之间线段最短得到CD'的长即为最短距离，求出CD′的解析式，即可求出E点坐标．
【解答】解：作D关于x轴的对称点D′，连接D′C，连接CD′交x轴于E，
△CDE的周长为CD+DE+EC＝CD+D′E+EC＝CD′+CD，
∵D为BO的中点，
∴BD＝OD＝2，
∵D和D′关于x轴对称，
∴D′（0，﹣2），
∴易得，C（3，4），
设直线CD'的解析式为y＝kx+b，
把C（3，4），D′（0，﹣2）分别代入解析式得，
，
解得，，
解析式为y＝2x﹣2，
当y＝0时，x＝1，
故E点坐标为（1，0）．

15．（3分）如图所示，A（﹣，0）、B（0，1）分别为x轴、y轴上的点，△ABC为等边三角形，点P（3，a）在第一象限内，且满足2S△ABP＝S△ABC，则a的值　或2+　．

【分析】过P点作PD⊥x轴，垂足为D，根据A（﹣，0）、B（0，1）求OA、OB，利用勾股定理求AB，可得△ABC的面积，利用S△ABP＝S△AOB+S梯形BODP﹣S△ADP，列方程求a．
【解答】解：过P点作PD⊥x轴，垂足为D，
由A（﹣，0）、B（0，1），得OA＝，OB＝1，
∵△ABC为等边三角形，
由勾股定理，得AB＝＝2，
∴S△ABC＝×2×＝，
又∵S△ABP＝S△AOB+S梯形BODP﹣S△ADP
＝××1+×（1+a）×3﹣×（+3）×a，
＝，
由2S△ABP＝S△ABC，得+3＝，
∴a＝．
当P在AB与x＝3交点的上方时，同理可求得a＝2+
故答案为：或2+．

三.解答题（共6题，共55分）
16．（8分）计算下列各式：
（1）；
（2）．
【分析】（1）先利用完全平方公式和平方差公式展开，然后合并即可；
（2）先把各二次根式化为最简二次根式，然后合并即可；
【解答】解：（1）原式＝9+6+2+4﹣3
＝12+6；
（2）原式＝﹣2
＝1﹣2
＝﹣1．
17．（8分）解方程：
（1）；
（2）．
【分析】（1）用方程①×2+②，消去未知数y，求出未知数x，再把x的值代入①求出y即可；
（2）方程①整理后，利用加减消元法解答即可．
【解答】解：（1），
①×2+②，得5x＝10，
解得x＝2，
把x＝2代入①，得y＝﹣2，
故方程组的解为；
（2）方程组整理，得，
②﹣①，得y＝﹣7，
把y＝﹣7代入①，得x＝26，
故方程组的解为．
18．（5分）如图，在直角坐标系内，已知点A（﹣1，0）．
（1）图中点B的坐标是 　（﹣3，4）　；
（2）点B关于原点对称的点D的坐标是 　（3，﹣4）　；点A关于y轴对称的点C的坐标是 　（1，0）　；
（3）在y轴上找一点F，使S△ACF＝S△ABC．那么点F的坐标为 　（0，﹣4）或（0，4）　．

【分析】（1）根据坐标的意义即可得出点B的坐标；
（2）根据关于原点对称的两个点坐标之间的关系可得出点B关于原点对称的点D的坐标，同理根据关于y轴对称的两个点坐标之间的关系得出点A关于y对称点C的坐标；
（3）根据等底等高的三角形的面积相等求解即可．
【解答】解：（1）过点B作x轴的垂线，垂足所对应的数为﹣3，因此点B的横坐标为﹣3，
过点B作y轴的垂线，垂足所对应的数为4，因此点B的纵坐标为4，
所以点B（﹣3，4）；
故答案为：（﹣3，4）；
（2）由于关于原点对称的两个点坐标纵横坐标均为互为相反数，
所以点B（﹣3，4）关于原点对称点C（3，﹣4），
由于关于y轴对称的两个点，其横坐标互为相反数，其纵坐标不变，
所以点A（﹣1，0）关于y轴对称点D（1，0），
故答案为：（3，﹣4），（1，0）；
（3）设点F的坐标为（0，y），

因为S△ABC＝＝4，S△ACF＝S△ABC，
所以|OF|＝4，
∴|OF|＝4，
解得y＝﹣4或4，
∴F的坐标为（0，﹣4）或（0，4）．
故答案为：（0，﹣4）或（0，4）．
19．（6分）大家知道，是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，而，于是可用来表示的小数部分．请解答下列问题：
（1）的整数部分是 　3　，小数部分是 　﹣3　；
（2）如果的整数部分为a，的小数部分为b，求的值．
【分析】（1）根据的大小得出结论即可；
（2）分别得出a和b的值，然后计算结果即可．
【解答】解：（1）∵3＜＜4，
∴的整数部分是3，小数部分是﹣3，
故答案为：3，﹣3；
（2）由题知，a＝5，b＝﹣2，
∴a+b﹣5
＝5+×（﹣2）﹣5
＝5+5﹣2﹣5
＝5﹣2．
20．（7分）某中学计划举行以“奋斗百年路，启航新征程”为主题的知识竞赛，并对获奖的同学给予奖励．现要购买甲、乙两种奖品，已知1件甲种奖品和2件乙种奖品共需40元，2件甲种奖品和3件乙种奖品共需70元．
（1）求甲、乙两种奖品的单价；
（2）根据颁奖计划，该中学需甲、乙两种奖品共60件，且甲种奖品不少于20件，应如何购买才能使总费用最少？并求出最少费用．
【分析】（1）设甲种奖品的单价为x元/件，乙种奖品的单价为y元/件，根据“购买1件甲种奖品和2件乙种奖品共需40元，购买2件甲种奖品和3件乙种奖品共需70元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设购买甲种奖品m件，则购买乙种奖品（60﹣m）件，设购买两种奖品的总费用为w，由甲种奖品不少于20件，可得出关于m的取值范围，再由总价＝单价×数量，可得出w关于m的函数关系式，利用一次函数的性质即可解决最值问题．
【解答】解：（1）设甲种奖品的单价为x元/件，乙种奖品的单价为y元/件，
依题意，得：，
解得，
答：甲种奖品的单价为20元/件，乙种奖品的单价为10元/件．
（2）设购买甲种奖品m件，则购买乙种奖品（60﹣m）件，设购买两种奖品的总费用为w元，
∵甲种奖品不少于20件，
∴m≥20．
依题意，得：w＝20m+10（60﹣m）＝10m+600，
∵10＞0，
∴w随m值的增大而增大，
∴当学校购买20件甲种奖品、40件乙种奖品时，总费用最少，最少费用是800元．
21．（8分）我们新定义一种三角形：两边平方和等于第三边平方的4倍的三角形叫做常态三角形．例如：某三角形三边长分别是5，6和8，因为62+82＝4×52＝100，所以这个三角形是常态三角形．
（1）若△ABC三边长分别是2，和4，则此三角形 　是　常态三角形（填“是”或“不是”）；
（2）若Rt△ABC是常态三角形，则此三角形的三边长之比为 　　；
（3）如图，Rt△ABC中，∠ACB＝90°，BC＝6，D在AB上，且AD＝BD＝CD，若△BCD是常态三角形，求线段AC的长．

【分析】（1）根据常态三角形的定义判定即可；
（2）根据常态三角形的定义以及勾股定理得出a：b＝：，即可求解；
（3）根据常态三角形的定义得出等式求出BD的长，再由勾股定理即可得出结果．
【解答】解：（1）∵2，
∴此三角形 是常态三角形，
故答案为：是；
（2）∵Rt△ABC是常态三角形，
∴设两直角边长为a，b，斜边长为c，
∴a2+b2＝c2，a2+c2＝4b2，
∴2a2＝3b2，
∴a：b＝：，
设a＝x，b＝x，
则c＝x，
∴此三角形的三边长之比为，
故答案为：；
（3）∵△BCD是常态三角形，
∴BD2+BC2＝4CD2，
∵BD＝CD，BC＝6，
∴BD2+62＝4BD2，
∴BD＝2（负值已舍），
∴AD＝BD＝2，
∴AB＝4，
在Rt△ABC中，由勾股定理得，
AC＝＝2．
22．（8分）如图，直线y＝2x+m（m＞0）与x轴交于点A（﹣2，0），直线y＝﹣x+n（n＞0）与x轴、y轴分别交于B、C两点，并与直线y＝2x+m（m＞0）相交于点D，若AB＝4．
（1）求直线BC的解析式；
（2）求出四边形AOCD的面积；
（3）若E为x轴上一点，且△ACE为等腰三角形，请直接写出点E的坐标．

【分析】（1）先把A点坐标代入y＝2x+m得到m＝4，则y＝2x+4，再利用AB＝4可得到B点坐标为（2，0），则把B点坐标代入y＝﹣x+n可得到n＝2，即可求得直线BC的解析式；
（2）通过解方程组得到D点坐标，确定C点坐标为（0，2），然后利用四边形AOCD的面积＝S△DAB﹣S△COB进行计算即可；
（3）先利用A、C两点的坐标特征得到△ACO为等腰直角三角形，AC＝2，然后分类讨论：当AE＝AC＝2时，以A点为圆心，2画弧交x轴于E1点和E2点，再写出它们的坐标；当CE＝CA时，E3点与点A关于y轴对称，即可得到它的坐标；当EA＝EC时，E4点为坐标原点．
【解答】解：（1）把A（﹣2，0）代入y＝2x+m得﹣4+m＝0，解得m＝4，
∴y＝2x+4，
∵AB＝4，A（﹣2，0），
∴B点坐标为（2，0），
把B（2，0）代入y＝﹣x+n得﹣2+n＝0，解得n＝2，
∴直线BC的解析式为y＝﹣x+2；
（2）解方程组得，
∴D点坐标为（﹣，），
当x＝0时，y＝﹣x+2＝2，
∴C点坐标为（0，2），
∴四边形AOCD的面积＝S△DAB﹣S△COB
＝×4×﹣×2×2
＝；
（3）∵A（﹣2，0），C（0，2），
∴AC＝2，
当AE＝AC＝2时，E1点的坐标为（2﹣2，0），E2点的坐标为（﹣2﹣2，0）；
当CE＝CA时，E3点的坐标为（2，0），
当EA＝EC时，E4点的坐标为（0，0），
综上所述，点E的坐标为（2﹣2，0）、（﹣2﹣2，0）、（2，0）、（0，0）．



APP 公众号 小程序