


广东省深圳市福田区深圳实验学校2022-2023学年七下数学期末学业水平测试模拟试题含答案
展开广东省深圳市福田区深圳实验学校2022-2023学年七下数学期末学业水平测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.如图,在菱形ABCD中,∠A=60°,E,F分别是AB,AD的中点,DE,BF相交于点G,连接BD,CG,有下列结论:①∠BGD=120° ;②BG+DG=CG;③△BDF≌△CGB;④![]() .其中正确的结论有( )
.其中正确的结论有( )
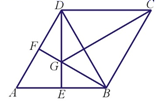
A.1个 B.2个 C.3个 D.4个
2.如果将分式![]() 中的
中的![]() 、
、![]() 都扩大2倍,那么分式的值( )
都扩大2倍,那么分式的值( )
A.不变 B.扩大2倍 C.缩小2倍 D.扩大4倍
3.若关于x的不等式组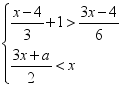 的解集为x<2,则a的取值范围是( )
的解集为x<2,则a的取值范围是( )
A.a≥﹣2 B.a>﹣2 C.a≤﹣2 D.a<﹣2
4.对于正比例函数 y 3x ,下列说法正确的是( )
A.y 随 x 的增大而减小 B.y 随 x 的增大而增大
C.y 随 x 的减小而增大 D.y 有最小值
5.如图,直线![]() 和直线
和直线![]() 相交于点
相交于点![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
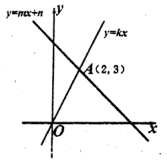
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知一次函数![]() 的图象不经过第三象限,则
的图象不经过第三象限,则![]() 、
、![]() 的符号是( )
的符号是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
7.在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在C边上的点E处,折痕为AF,点F在BC边上;②把△ADH翻折,点D落在AE边上的点G处,折痕为AH,点H在CD边上,若AD=6,CD=10,则![]() =( )
=( )
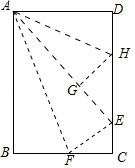
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若一个三角形的三边长为![]() ,则使得此三角形是直角三角形的的值是( )
,则使得此三角形是直角三角形的的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
9.如图,直线l所表示的变量x,y之间的函数关系式为![]()
![]()
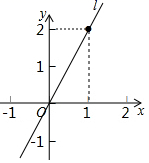
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,平行四边形ABCD中,AC⊥AB,点E为BC边中点,AD=6,则AE的长为( )
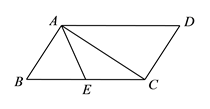
A.2 B.3 C.4 D. 5
二、填空题(本大题共有6小题,每小题3分,共18分)
11.每本书的厚度为![]() ,把这些书摞在一起总厚度
,把这些书摞在一起总厚度![]() (单位:
(单位:![]() 随书的本数
随书的本数![]() 的变化而变化,请写出
的变化而变化,请写出![]() 关于
关于![]() 的函数解析式__,(不用写自变量的取值范围)
的函数解析式__,(不用写自变量的取值范围)
12.已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2,若x1,x2满足3x1=|x2|+2,则m的值为_____
13.若代数式![]() 有意义,则
有意义,则![]() 的取值范围为__________.
的取值范围为__________.
14.计算![]() 的结果是__________.
的结果是__________.
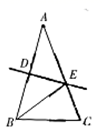
15.如图,等腰![]() 中,
中,![]() ,
,![]() ,线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于______.
,线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于______.
16.已知y=xm-2+3是一次函数,则m=________ .
三、解下列各题(本大题共8小题,共72分)
17.(8分)先化简,再求值:![]() ,其中x=1.
,其中x=1.
18.(8分)阅读例题,解答下题.
范例:解方程: x2 + ∣x +1∣﹣1= 0
解:(1)当 x+1 ≥ 0,即 x ≥ ﹣1时,
x2 + x +1﹣1= 0
x2 + x = 0
解得 x 1 = 0 ,x2 =﹣1
(2)当 x+1 < 0,即 x < ﹣1时,
x2 ﹣ ( x +1)﹣1= 0
x2﹣x ﹣2= 0
解得x 1 =﹣1 ,x2 = 2
∵ x < ﹣1,∴ x 1 =﹣1,x2 = 2 都舍去.
综上所述,原方程的解是x1 = 0,x2 =﹣1
依照上例解法,解方程:x2﹣2∣x-2∣-4 = 0
19.(8分)如图,四边形![]() 是平行四边形,
是平行四边形,![]() 为
为![]() 上一点,连接
上一点,连接![]() 并延长,使
并延长,使![]() ,连接
,连接![]() 并延长,使
并延长,使![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
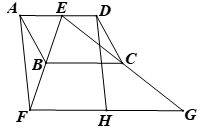
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
20.(8分)我们将![]() 、
、![]() 称为一对“对偶式”,因为
称为一对“对偶式”,因为![]() ,所以构造“对偶式”再将其相乘可以有效的将
,所以构造“对偶式”再将其相乘可以有效的将![]() 和
和![]() 中的“
中的“![]() ”去掉.于是二次根式除法可以这样解:如
”去掉.于是二次根式除法可以这样解:如![]() ,
,![]() .像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.根据以上材料,理解并运用材料提供的方法,解答以下问题:
.像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)比较大小![]() ________
________![]() (用“
(用“![]() ”、“
”、“![]() ”或“
”或“![]() ”填空);
”填空);
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)计算:![]()
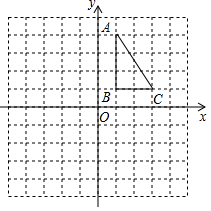
21.(8分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
22.(10分)如图1,在正方形ABCD中,点E、F分别是边BC、CD上的点,且CE=CF,连接AE,AF,取AE的中点M,EF的中点N,连接BM,MN.
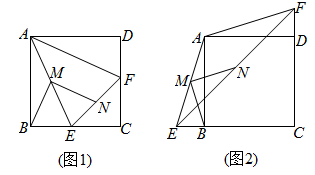
(1)请判断线段BM与MN的数量关系和位置关系,并予以证明.
(2)如图2,若点E在CB的延长线上,点F在CD的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
23.(10分)如图,四边形![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一定角度后,点
顺时针旋转一定角度后,点![]() 的对应点恰好与点
的对应点恰好与点![]() 重合,得到
重合,得到![]() .
.
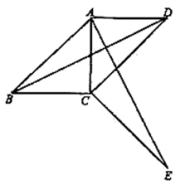
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,
,![]() ,试求出四边形
,试求出四边形![]() 的对角线
的对角线![]() 的长.
的长.
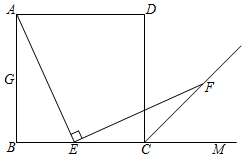
24.(12分)如图,四边形ABCD是正方形,点E是BC边上的点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)如图①,当点E是BC边上任一点(不与点B、C重合)时,求证:AE=EF.
(2)如图②当点E是BC边的延长线上一点时,(1)中的结论还成立吗? (填成立或者不成立).
(3)当点E是BC边上任一点(不与点B、C重合)时,若已知AE=EF,那么∠AEF的度数是否发生变化?证明你的结论.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、C
4、B
5、C
6、C
7、A
8、D
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、2
13、![]() 且
且![]() .
.
14、![]()
15、45°
16、3
三、解下列各题(本大题共8小题,共72分)
17、![]() ,
,![]()
18、 (1) x 1 = 0 , x2 = 2;(2)x1 = 2 ,x2 =﹣4.
19、(1)见解析;(2)![]() .
.
20、(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
21、(1)作图见解析;(2)作图见解析;(3)2π.
22、(1)BM=MN,BM⊥MN,证明见解析;(2)仍然成立,证明见解析
23、(1)![]() 是等腰直角三角形,理由详见解析;(2)
是等腰直角三角形,理由详见解析;(2)![]()
24、(1)见解析;(2)成立,理由见解析;(3)∠AEF=90°不发生变化.理由见解析.
广东省深圳市福田区耀华实验学校2023-2024学年八上数学期末学业水平测试模拟试题含答案: 这是一份广东省深圳市福田区耀华实验学校2023-2024学年八上数学期末学业水平测试模拟试题含答案,共7页。试卷主要包含了下列图形中,不是轴对称图形的是等内容,欢迎下载使用。
广东省深圳市深圳实验学校2022-2023学年数学七下期末综合测试模拟试题含答案: 这是一份广东省深圳市深圳实验学校2022-2023学年数学七下期末综合测试模拟试题含答案,共6页。
广东省深圳市福田区耀华实验学校2022-2023学年数学七下期末达标测试试题含答案: 这是一份广东省深圳市福田区耀华实验学校2022-2023学年数学七下期末达标测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,六边形的内角和为,已知点,下列根式中不是最简二次根式的是等内容,欢迎下载使用。












