



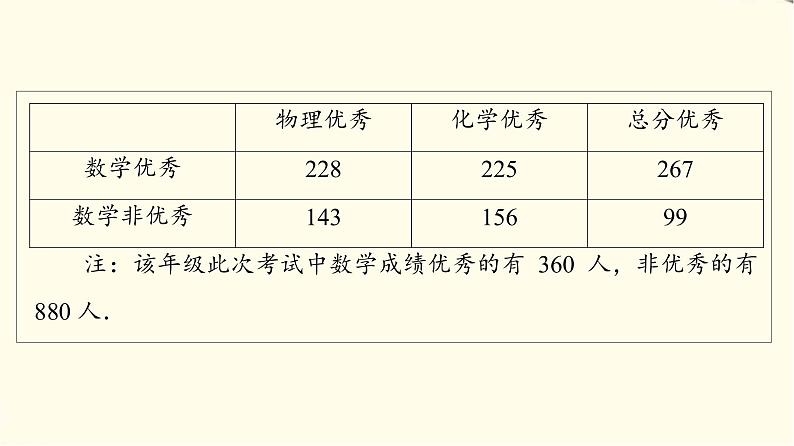

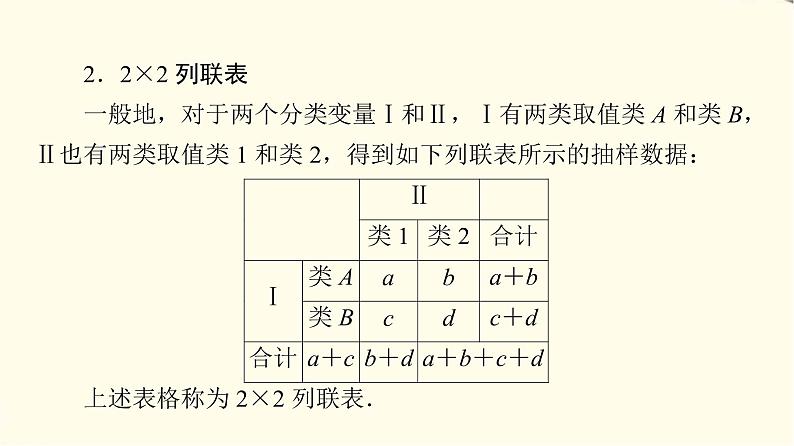







高中数学苏教版 (2019)选择性必修第二册9.2独立性检验图文ppt课件
展开课后素养落实(三十) 独立性检验
(建议用时:40分钟)
一、选择题
1.(多选题)给出下列实际问题,其中用独立性检验可以解决的问题有( )
A.一种药物对某种病的治愈率
B.两种药物治疗同一种病是否有区别
C.吸烟与性别是否有关系
D.去网吧与青少年的犯罪是否有关系
BCD [独立性检验是判断两个分类变量是否有关系的方法,而A是概率问题,不能用独立性检验解决,BCD都可以.]
2.某科研机构为了研究中年人秃发与心脏病是否有关,随机调查了一些中年人的情况,具体数据如表:
| 心脏病 | 无心脏病 |
秃发 | 20 | 300 |
不秃发 | 5 | 450 |
根据表中数据得到χ2=≈15.968,因为χ2>6.635,则推断秃发与心脏病有关系,那么这种判断出错的可能性为( )
A.0.1 B.0.05
C.0.025 D.0.01
D [∵χ2>6.635,对照临界值表可知选D.]
3.根据下面的2×2列联表计算出χ2=( )
| 优秀生 | 非优秀生 |
男生 | 15 | 45 |
女生 | 15 | 25 |
A. B.
C. D.
A [根据题意补充列联表如下:
| 优秀生 | 非优秀生 | 合计 |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
计算χ2=
==.]
4.在独立性检验中,两个分类变量“X与Y有关系”的可信度为99%,则χ2统计量的取值范围是( )
A.[3.841,5.024) B.[5.024,6.635)
C.[6.635,7.879) D.[7.879,10.828)
C [假设不成立的概率为0.01,对照临界值表可知χ2统计量的取值范围是[6.635,7.879).]
5.(多选题)因防疫的需要,多数大学开学后启用封闭式管理.某大学开学后也启用封闭式管理,该校有在校学生9 000人,其中男生4 000人,女生5 000人,为了解学生在封闭式管理期间对学校的管理和服务的满意度,随机调查了40名男生和50名女生,每位被调查的学生都对学校的管理和服务给出了满意或不满意的评价,经统计得到如下列联表:
| 满意 | 不满意 |
男 | 20 | 20 |
女 | 40 | 10 |
以下说法正确的有( )
A.满意度的调查过程采用了分层抽样的抽样方法
B.该学校学生对学校的管理和服务满意的概率的估计值为0.6
C.有99%的把握认为学生对学校的管理和服务满意与否与性别有关系
D.没有99%的把握认为学生对学校的管理和服务满意与否与性别有关系
AC [因为男女比例为4 000︰5 000,故A正确.满意的频率为=≈0.667,所以该学校学生对学校的管理和服务满意的概率的估计值约为0.667,所以B错误.
由列联表χ2==9>6.635,故有99%的把握认为学生对学校的管理和服务满意与否与性别有关系,所以C正确,D错误.]
二、填空题
6.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算χ2的值知χ2≈27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病是________的.(填“有关”或“无关”)
有关 [由χ2≈27.63与临界值比较,我们有99.9%的把握说打鼾与患心脏病有关.]
7.下表是关于男婴与女婴出生时间调查的列联表:
| 晚上 | 白天 | 总计 |
男婴 | 45 | A | B |
女婴 | E | 35 | C |
总计 | 98 | D | 180 |
那么,A=________,B=________,C=________,
D=________,E=________.
47 92 88 82 53 [由列联表知识得
解得]
8.利用独立性检验来考虑两个分类变量X与Y是否有关系时,通过查阅下表来确定“X和Y有关系”的可信度.如果χ2的值χ2>5.024,那么在犯错误的概率不超过________的前提下认为“X和Y有关系”.
α | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
χα | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
0.025 [因为χ2的值χ2>5.024,而在临界值表中对应于5.024的是0.025,所以可以在犯错误的概率不超过0.025的前提下认为“X和Y有关系”.]
三、解答题
9.在对人们休闲方式的一次调查中,仅就看电视与运动这两种休闲方式比较喜欢哪一种进行了调查.调查结果:接受调查总人数110人,其中男、女各55人;受调查者中,女性有30人比较喜欢看电视,男性有35人比较喜欢运动.
(1)请根据题目所提供的调查结果填写下列2×2列联表:
| 看电视 | 运动 | 合计 |
女 |
|
|
|
男 |
|
|
|
合计 |
|
|
|
(2)能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”?
注:χ2=(其中n=a+b+c+d为样本容量)
P(χ2≥x0) | 0.10 | 0.05 | 0.025 | 0.010 |
x0 | 2.706 | 3.841 | 5.024 | 6.635 |
[解] (1)根据题目所提供的调查结果,可得下列2×2列联表:
| 看电视 | 运动 | 合计 |
女 | 30 | 25 | 55 |
男 | 20 | 35 | 55 |
合计 | 50 | 60 | 110 |
(2)提出假设H0:性别与休闲方式无关.
根据列联表中的数据,可计算χ2=≈3.667,
因为3.667<3.841,所以不能在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”.
10.某校数学课外兴趣小组为研究数学成绩是否与性别有关,统计了本校高三年级每名学生一学期数学成绩的平均分 (采用百分制),剔除平均分在 40分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100 名学生,按性别分为两组,并将两组学生的成绩分为6组,得到下表.
分数段 性别 | [40, 50] | [50, 60] | [60, 70] | [70, 80] | [80, 90] | [90, 100] |
男/人 | 3 | 9 | 18 | 15 | 6 | 9 |
女/人 | 6 | 4 | 5 | 10 | 13 | 2 |
附表及公式:其中n=a+b+c+d,
χ2=.
α | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
χα | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果判断数学成绩与性别是否有关;
(2)规定成绩在80分以上为优秀(含80分),请你根据已知条件补全所列的2×2列联表,并判断能否在犯错误的概率不超过0.1的前提下认为“数学成绩与性别有关”?
| 优秀 | 非优秀 | 合计 |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
[解] (1)男生的平均分1=
=71.5,
女生的平均分2=
=71.5,
从男、女生各自的平均分来看,数学成绩与性别无关.
(2)由题表可知, 在抽取的100名学生中,男生组中成绩优秀的有15人,女生组中成绩优秀的有15人,据此可得2×2列联表.
| 优秀 | 非优秀 | 合计 |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
提出假设H0:数学成绩与性别无关,
计算可得χ2=≈1.786<2.706,
所以不能在犯错误的概率不超过0.1的前提下认为“数学成绩与性别有关”.
11.(多选题)在研究打鼾与患心脏病之间的关系中,通过收集数据、整理分析数据得到“打鼾与患心脏病有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的.下列说法中正确的是( )
A.100个心脏病患者中至少有99人打鼾
B.打鼾与患心脏病有关
C.100个心脏病患者一定有打鼾的人
D.100个心脏病患者可能一个打鼾的人都没有
BD [这是独立性检验,在犯错误的概率不超过0.01的前提下认为“打鼾与患心脏病有关”.这只是一个概率,即打鼾与患心脏病有关的可能性为99%.根据概率的意义可知应选BD.]
12.(多选题)在一次恶劣气候的飞行航程中,调查男女乘客在机上晕机的情况,如下表所示:
| 晕机 | 不晕机 | 合计 |
男 | n11 | 15 | n1+ |
女 | 6 | n22 | n2+ |
合计 | n+1 | 28 | 46 |
则下列说法正确的是( )
A.>
B.χ2<2.706
C.有90%的把握认为,在恶劣气候飞行中,晕机与否跟男女性别有关
D.没有理由认为,在恶劣气候飞行中,晕机与否跟男女性别有关
ABD [由列联表数据,知,得.
∴==>=,即A正确;
| 晕机 | 不晕机 | 合计 |
男 | 12 | 15 | 27 |
女 | 6 | 13 | 19 |
合计 | 18 | 28 | 46 |
∴χ2=≈0.775<2.706,即B正确;
且没有理由认为,在恶劣气候飞行中,晕机与否跟男女性别有关,即D正确.]
13.为了研究高三年级学生的性别和身高是否大于170 cm有关的问题,得到某中学三年级学生的性别和身高的所有观测数据所对应的列联表如下:
单位:人
性别 | 身高 | 合计 | |
低于170 cm | 不低于170 cm | ||
女 | 81 | 16 | 97 |
男 | 28 | 75 | 103 |
合计 | 109 | 91 | 200 |
进行统计分析时的假设为________.
性别与身高是否大于170 cm之间无关联 [由独立性检验的步骤知第一步先假设两个分类变量相互独立,即进行统计分析时的假设为性别与身高是否大于170 cm之间无关联.]
14.为研究某新药的疗效,给50名患者服用此药,跟踪调查后得下表中的数据:
| 无效 | 有效 | 总计 |
男性患者 | 15 | 35 | 50 |
女性患者 | 6 | 44 | 50 |
总计 | 21 | 79 | 100 |
设H0:服用此药的效果与患者性别无关,则χ2≈______,从而得出结论:服用此药的效果与患者的性别有关,这种判断出错的可能性为________.
4.882 5% [由公式计算得χ2≈4.882,
∵4.882>3.841,∴有95%的把握认为服用此药的效果与患者的性别有关,从而有5%的可能性出错.]
15.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分 组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98, 30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频 数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分 组 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
频 数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)完成下列的列联表并依据小概率值α=0.01的独立性检验,分析甲厂和乙厂生产的零件是否有差异?
产品 | 生产工厂 | 合计 | |
甲厂 | 乙厂 | ||
优质品 |
|
|
|
非优质品 |
|
|
|
合计 |
|
|
|
[解] (1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为=64%.
(2)2×2列联表如下:
产品 | 生产工厂 | 合计 | |
甲厂 | 乙厂 | ||
优质品 | 360 | 320 | 680 |
非优质品 | 140 | 180 | 320 |
合计 | 500 | 500 | 1000 |
提出假设H0:两个分厂生产的零件无差异,
根据表中数据知χ2=≈7.353,
因为H0成立时,χ2≥6.635的概率为0.010,
这里的χ2≈7.353>6.635,所以我们有99%的把握认为,两个分厂生产的零件质量有差异.
高中数学苏教版 (2019)选择性必修第二册9.2独立性检验评优课ppt课件: 这是一份高中数学苏教版 (2019)选择性必修第二册9.2独立性检验评优课ppt课件,共20页。PPT课件主要包含了随堂小测等内容,欢迎下载使用。
高中数学8.2离散型随机变量及其分布列图片ppt课件: 这是一份高中数学8.2离散型随机变量及其分布列图片ppt课件,文件包含苏教版高中数学选择性必修第二册第8章824超几何分布课件ppt、苏教版高中数学选择性必修第二册第8章824超几何分布学案doc、苏教版高中数学选择性必修第二册课后素养落实27超几何分布含答案doc等3份课件配套教学资源,其中PPT共43页, 欢迎下载使用。
高中数学苏教版 (2019)选择性必修第二册8.1条件概率教课ppt课件: 这是一份高中数学苏教版 (2019)选择性必修第二册8.1条件概率教课ppt课件,文件包含苏教版高中数学选择性必修第二册第8章812全概率公式课件ppt、苏教版高中数学选择性必修第二册第8章812全概率公式学案doc、苏教版高中数学选择性必修第二册课后素养落实21全概率公式含答案doc等3份课件配套教学资源,其中PPT共39页, 欢迎下载使用。













