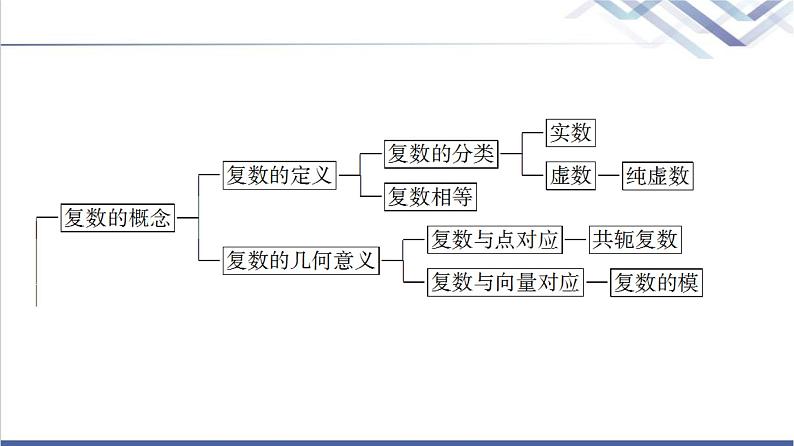
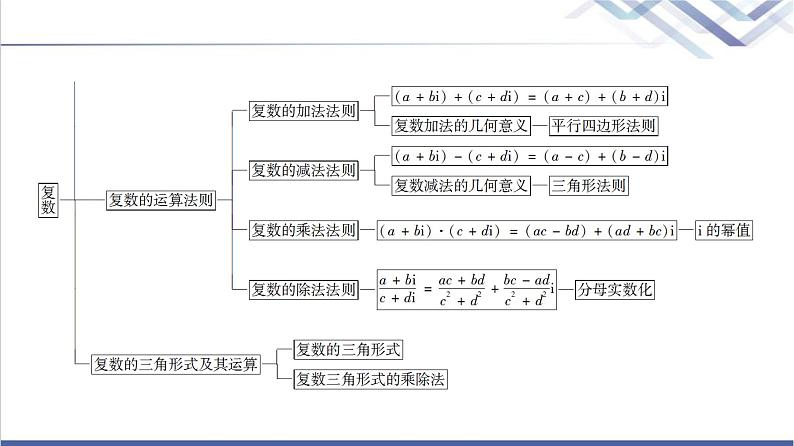
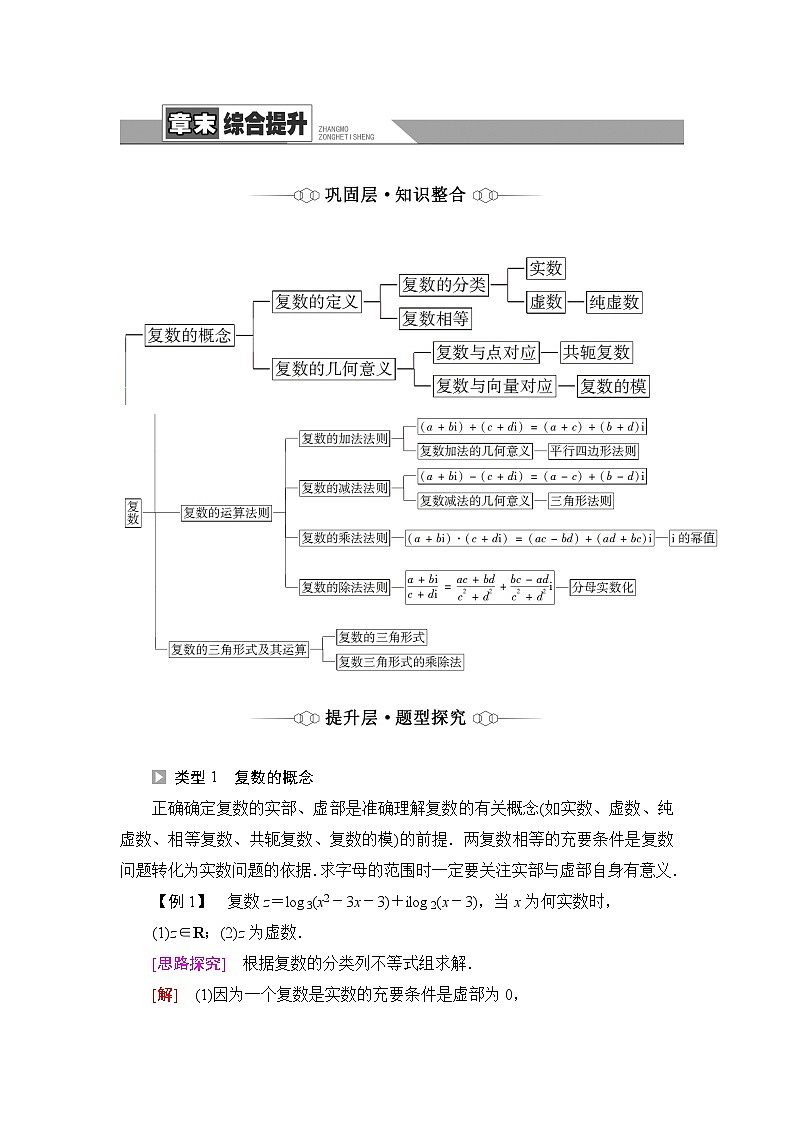
人教B版高中数学必修第四册第10章章末综合提升课件+学案

类型1　复数的概念

正确确定复数的实部、虚部是准确理解复数的有关概念(如实数、虚数、纯虚数、相等复数、共轭复数、复数的模)的前提．两复数相等的充要条件是复数问题转化为实数问题的依据．求字母的范围时一定要关注实部与虚部自身有意义．

【例1】　复数z＝log3(x2－3x－3)＋ilog2(x－3)，当x为何实数时，

(1)z∈R；(2)z为虚数．

[思路探究]　根据复数的分类列不等式组求解．

[解]　(1)因为一个复数是实数的充要条件是虚部为0，

所以

由②得x＝4，经验证满足①③式．

所以当x＝4时，z∈R．

(2)因为一个复数是虚数的充要条件是虚部不为0，

所以

由①得x>或x<．

由②得x≠4，由③得x>3．

所以当x>且x≠4时，z为虚数．

1．(1)若复数z满足(3－4i)z＝|4＋3i|，则z的虚部为(　　)

A．－4      B．－    C．4      D．

(2)设复数z满足i(z＋1)＝－3＋2i(i是虚数单位)，则复数z的实部是__________．

(1)D　(2)1　[(1)∵(3－4i)z＝|4＋3i|，∴z＝＝＝＝＋i，

∴z的虚部为．故选D．

(2)法一：设z＝a＋bi(a，b∈R)，

则i(z＋1)＝i(a＋bi＋1)＝－b＋(a＋1)i＝－3＋2i．

由复数相等的充要条件，得解得

故复数z的实部是1．

法二：由i(z＋1)＝－3＋2i，得z＋1＝＝2＋3i，故z＝1＋3i，即复数z的实部是1．]

类型2　复数的四则运算

复数加减乘运算可类比多项式的加减乘运算，注意把i看作一个字母(i2＝－1)，除法运算注意应用共轭的性质z·为实数．

【例2】　(1)设i是虚数单位，表示复数z的共轭复数．若z＝1＋i，则＋i·＝(　　)

A．－2      B．－2i    C．2      D．2i

(2)设复数z满足(z－2i)(2－i)＝5，则z＝(　　)

A．2＋3i      B．2－3i    C．3＋2i      D．3－2i

[思路探究]　(1)先求出及，结合复数运算法则求解．

(2)利用方程思想求解并化简．

(1)C　(2)A　[(1)∵z＝1＋i，∴＝1－i，＝＝＝1－i，∴＋i·＝1－i＋i(1－i)＝2．故选C．

(2)由(z－2i)(2－i)＝5，得z＝2i＋＝2i＋＝2i＋2＋i＝2＋3i．]

2．(1)复数的共轭复数是(　　)

A．－i      B．i    C．－i      D．i

(2)已知复数z1＝(1＋i)(i为虚数单位)，复数z2的虚部为2，且z1·z2是实数，则z2＝________．

(1)C　(2)4＋2i　[(1)依题意知，＝＝＝i，

∴其共轭复数为－i．

(2)z1＝(1＋i)＝2－i．

设z2＝a＋2i，a∈R，

则z1·z2＝(2－i)·(a＋2i)

＝(2a＋2)＋(4－a)i．

因为z1·z2∈R，

所以a＝4，

所以z2＝4＋2i．]

类型3　复数的几何意义

【例3】　(1)在复平面内，复数对应的点位于(　　)

A．第一象限       B．第二象限   

C．第三象限       D．第四象限

(2)在复平面内，复数对应的点的坐标为(　　)

A．(0，－1)   B．(0,1)

C．   D．

[思路探究]　先把复数z化为复数的标准形式，再写出其对应坐标．

(1)B　(2)A　[(1)复数＝＝＝－＋i．

∴复数对应点的坐标是．

∴复数在复平面内对应的点位于第二象限．故选B．

(2)∵＝＝＝－i，其对应的点为(0，－1)，故选A．]

3．(1)已知复数z对应的向量如图所示，则复数z＋1所对应的向量表示正确的是(　　)

(2)若i为虚数单位，图中复平面内点Z表示复数z，则表示复数的点是(　　)

A．E      B．F    C．G      D．H

(1)A　(2)D　[(1)由题图知，z＝－2＋i，∴z＋1＝－2＋i＋1＝－1＋i，故z＋1对应的向量应为选项A．

(2)由题图可得z＝3＋i，所以＝＝＝＝2－i，则其在复平面上对应的点为H(2，－1)．]

类型4　函数与方程思想

一般设出复数z的代数形式，即z＝x＋yi(x，y∈R)，则涉及复数的分类、几何意义、模的运算、四则运算、共轭复数等问题，都可以转化为实数x，y应满足的方程(组)，即复数问题实数化的思想是本章的主要思想方法．

【例4】　已知f(z)＝|1＋z|－，且f(－z)＝10＋3i，求复数z．

[思路探究]　设z＝a＋bi(a，b∈R)，则＝a－bi，由复数相等列方程组求解即可．

[解]　∵f(z)＝|1＋z|－，∴f(－z)＝|1－z|＋．

设z＝a＋bi(a，b∈R)，则＝a－bi．

由f(－z)＝10＋3i，得|1－(a＋bi)|＋a－bi＝10＋3i，

∴

解方程组得

∴复数z＝5－3i．

4．满足z＋是实数，且z＋3的实部与虚部是相反数的虚数z是否存在？若存在，求出虚数z；若不存在，请说明理由．

[解]　设虚数z＝x＋yi(x，y∈R，且y≠0)，

则z＋＝x＋yi＋＝x＋＋i，z＋3＝(x＋3)＋yi．

由已知，得因为y≠0，

所以解得或

所以存在虚数z＝－1－2i或z＝－2－i满足题设条件．

1．(2020·全国卷Ⅰ)若z＝1＋2i＋i3，则|z|＝(　　)

A．0      B．1    C．      D．2

C　[z＝1＋2i＋i3＝1＋2i－i＝1＋i，所以|z|＝＝，故选C．]

2．(2020·全国卷Ⅱ)(1－i)4＝(　　)

A．－4      B．4    C．－4i　      D．4i

A　[(1－i)4＝[(1－i)2]2＝(－2i)2＝－4，故选A．]

3．(2020·全国卷Ⅲ)复数的虚部是(　　)

A．－      B．－    C．      D．

D　[＝＝＝＋i，

所以虚部为．]

4．(2020·新高考全国卷Ⅰ)＝(　　)

A．1      B．－1    C．i      D．－i

D　[法一：＝＝＝－i，选D．

法二：利用i2＝－1进行替换，则＝＝＝＝－i，选D．]

5．(2020·北京高考)在复平面内，复数z对应的点的坐标是(1,2)，则i·z＝(　　)

A．1＋2i      B．－2＋i    C．1－2i      D．－2－i

B　[由题意知，z＝1＋2i，所以i·z＝i·(1＋2i)＝－2＋i，故选B．]

6．(2020·浙江高考)已知a∈R，若a－1＋(a－2)i(i为虚数单位)是实数，则a＝(　　)

A．1      B．－1    C．2      D．－2

C　[因为a－1＋(a－2)i是实数，所以a－2＝0，所以a＝2．故选C．]

7．(2020·全国卷Ⅱ)设复数z1，z2满足|z1|＝|z2|＝2，z1＋z2＝＋i，则|z1－z2|＝________．

2　[法一：设z1＝x1＋y1i(x1，y1∈R)，z2＝x2＋y2i(x2，y2∈R)，则由|z1|＝|z2|＝2，得x＋y＝x＋y＝4．

因为z1＋z2＝x1＋x2＋(y1＋y2)i＝＋i，所以|z1＋z2|2＝(x1＋x2)2＋(y1＋y2)2＝x＋y＋x＋y＋2x1x2＋2y1y2＝8＋2x1x2＋2y1y2＝()2＋12＝4，所以2x1x2＋2y1y2＝－4，所以|z1－z2|＝|x1－x2＋(y1－y2)i|＝＝

＝＝2．

法二：设z1＝a＋bi(a，b∈R)，

则z2＝－a＋(1－b)i，

则

即

所以|z1－z2|2＝(2a－)2＋(2b－1)2＝4(a2＋b2)－4(a＋b)＋4＝4×4－4×2＋4＝12，所以|z1－z2|＝2．

法三：题设可等价转化为向量a，b满足|a|＝|b|＝2，a＋b＝(，1)，求|a－b|．因为(a＋b)2＋(a－b)2＝2|a|2＋2|b|2，所以4＋(a－b)2＝16，所以|a－b|＝2，即|z1－z2|＝2．]