江苏省宿迁市钟吾初级中学2022-2023学年八年级上学期数学期中测试卷 (含答案)

这是一份江苏省宿迁市钟吾初级中学2022-2023学年八年级上学期数学期中测试卷 (含答案)，共18页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

试卷满分:150分 考试时间:120分钟
一、选择题(每小题3分，共8题，计24分)
1.下面是科学防控新冠知识的图片，其中的图案是轴对称图形的是( )
2.如图，若△ABC≌ΔADE，则下列结论中一定成立的是( )
A. AC=DE B.∠BAD=∠CAE C.AB=AE D. ∠ABC=∠AED
第2题图
3.已知△ABC的三条边分别为a、b、c，三个内角分别为∠A、∠B、∠C，则满足下列条件的ΔABC不是直角三角形的是( )
A.a=1,b=2,c=3 B.a2-c2=b2 C. ∠A=2∠B=3∠C D. ∠A-∠B=∠C
4.若一个自然数的算术平方根是a，则比它大1的数的算术平方根是( )
A. a+1 B.a2+1 C.a+1 D.a1+1
5.如图，在△ABC中，已知点D，E，F分别为AC，BD，CE的中点，且阴影部分图形面积等于4平方厘米，则ΔABC的面积为( )平方厘米
A.8 B.12 C. 16 D.18
第5题图
6.如图，在Rt△ABC中，∠ACB=90°，∠A=60°，过点C的直线与AB 交于点D，且将△ABC的面积分成相等的两部分，则∠CDA=( )
A. 30° B. 45° C. 60° D. 75°
第6題圏
7. “赵爽弦图”巧妙地利用面积关系证明子勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若(a+b)2=21，大正方形的面积为 13，则小正方形的面积为（ ）
A.3 B. 4 C.5 D. 6
第7题图
8.如图，在△ABC中，4D⊥BC，∠B=62°, AB+BD=CD，则∠BAC的度数为（ ）
A. 90° B. 89° C. 88° D. 87°
第8题图
二、选择题（每小题3分，共10题，计30分）
9.16 的平方根是
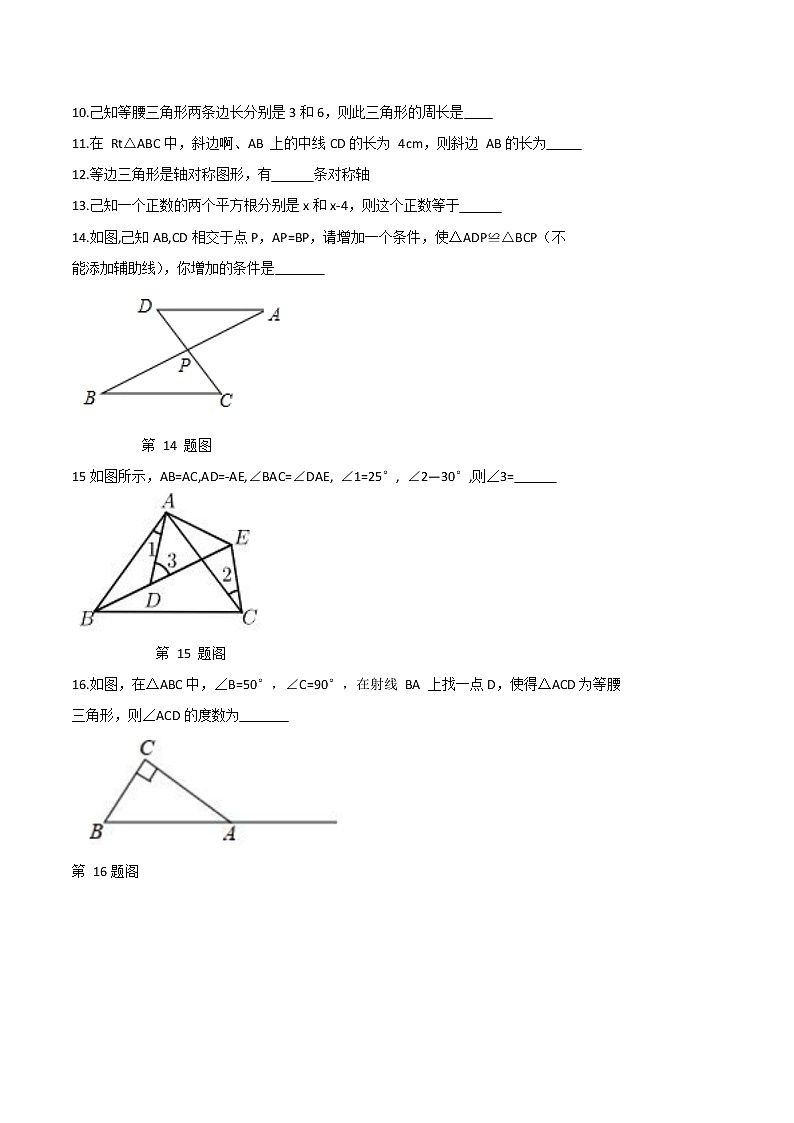
10.己知等腰三角形两条边长分别是3和6，则此三角形的周长是
11.在 Rt△ABC中，斜边啊、AB 上的中线CD的长为 4cm，则斜边 AB的长为
12.等边三角形是轴对称图形，有 条对称轴
13.己知一个正数的两个平方根分别是x和x-4，则这个正数等于
14.如图,己知AB,CD相交于点P，AP=BP，请增加一个条件，使△ADP≌△BCP（不
能添加辅助线），你増加的条件是
第 14 题图
15如图所示，AB=AC,AD=-AE,∠BAC=∠DAE, ∠1=25°, ∠2—30°,则∠3=
第 15 题阁
16.如图，在△ABC中，∠B=50°，∠C=90°，在射线 BA 上找一点D，使得△ACD为等腰
三角形，则∠ACD的度数为
第 16题阁
17.如图，△ABC 的三边 AB，CA，BC的长分别为 40，50，60，其三条角平分线交于点0，则 S△ABO: S△BCO: S△CAO =
第17题图
18.己知一张三角形纸片 ABC（如图甲），其中 AB=AC：将纸片沿过点 B的直线折登，使点C落到AB 边上的上点E处，折痕为 BD（如图乙）。再将纸片沿过点E的直线折香，点A恰好与点D重合，折痕为EF（如图丙)．原三角形纸片 ABC中，∠ABC的大小为
第18题图
三、解答题（共10题，计96分）
12 （8分）计算：4-3-π0+（13）-2
20.（8分）解下列方程：16x2=49.
21.（8分）如图，己知BE⊥CD,BE=DE, BC=AD.
（1）求证：△BEC ≌△DEA;
（2）求∠DFC的度数。
第 21 题图
22. (8分）己知 6a+34 的立方根是4，5a+b-2的算术平方根是5，c是9的算术平方根，
(1) 求a，b，c的值
(2) 求3a-b+c 的平方根.
23.（10 分）如图，在正方形网格中，每个小正方形的边长都为 1，网格中有一个格点△ABC（即三角形的顶点都在格点上）
（1）在图中作出△ABC 关于直线对称的△A1B1C1（点A的对应点是点A1，点B的对应点是点B1，点C的对应点是点C1）
(2) 在直l上画出点P， 使 PA+PC 最小
(3) 直接写出△A1B1C1的面积为

24. (10分）如图，四边形 ABCD中，∠ABC=∠ADC=90°，E是对角线 AC的中点，连接BE、DE.若AC=10,BD=8, 求△BDE的周长
25.（10分）如图，在△ABC中，∠C=90°.
（1）用尺规作图，保留作图痕迹，不写作法：在边 BC 上求作一点D，使得点D到 AB 的距离等于DC的长;
(2）在（1）的条件下，若 AC=6， AB=10，求CD的长
20 （10 分）公股定理神奇而美丽，它的证法多种多样，在学习了教材中介绍的拼图证法以后，小华突发灵感，给出了如图拼图：两个全等的直角三角板 ABC 和直角三角板 DEF，顶点F在BC边止，项点C、D重合，连接AE、EB.设 AB、DE交于点G. ∠ACB= ∠DFE=90°，BC=EF=a, AC=DF=b （a>b），AB=DE=c． 请你回答以下问题：
（1）请猜想AB 与DE的位置关系，并加以证明。
（2）填空：S四边形ADBE= （用含有c的代数式表示）
(3）请尝试利用此图形证明勾股定理。
27.（12分）（1）如图，在公△ABC中，∠BAC=90°，AB=AC，点D在BC上，且BD=BA，点E在BC的延长线上，且 CE=CA，求∠DAE 的度数：
(2）如果把第（1）题中“AB=AC”条件删去，其余条件不变，那么∠DAE 的度数改变吗？试证明；
(3）如果把(1)题中“∠BAC=90°的条件改为“∠BAC>90°，其余条件不变，,试探究∠DAE与∠BAC的数量关系式，试证明
28. （12 分）
【了解概念】
如图1，在△ABC和△ADE，AB=AC, AD=AE， ∠BAC=∠DAE，连接CE，连接BD
并延长与CE交于点F，那么将∠BFC叫做△ABC 和公△ADE的底联角。
【探究归纳】
（1）两个等腰三角形的底联角与这两个等腰三角形的顶角有怎样的数量关系？请用文字语言写出结论。
【拓展提升】
运用 （1）中的结论解决问题：
（2）如图2,AB=AC.AD=AE, ∠BAC=∠DAE=90°，∠DCE=62°，求∠BDC 的度数：
（3）如图3，在四边形 ABCD中，AB=6,BC=4，CD=5，点0为四边形ABCD 内一点,且OA=0B, 0C-=0D, ∠AOB=∠C0D=90°，求AD的长。
参考答案
选择题
1-8 ABCDCCCD
填空题
9、±4
10、15
11、8
12、3
13、4
14、DP=PC
15、55°
16、70°20°40°
17、4：6：5
18、72°
三、解答题
19 、 10
20、±74
21、
22、
（1）a=5;b=2;c=3
（2）16
23、
24、
25、（1）
26、
27、（1）
（2）
（3）
28、（1）
（2）