

山东省济南市历城区2022-2023学年九年级上学期数学期中 试题(含答案)
展开九年级上学期数学期中考试试题
满分150分 时间:150分钟
一.单选题。(每小题4分,共40分)
1.若ab=53,则a-bb的值为( )
A.43 B.23 C.35 D.25
2.下列几何体中,其俯视图与主视图完全相同的是( )
A. B. C. D.
3.若x=1是方程x2+mx+3=0的一个根,则方程的另一根是( )
A.3 B.4 C.﹣3 D.﹣4
4.如图,矩形ABCD中,对角线AC,BD交于点O,添加下面一个条件,能使矩形ABCD为正方形的是( )
A.BD=AB B.DC=AD C.∠AOB=60° D.OD=CD
(第4题图) (第5题图) (第6题图)
5.如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )
A.2 B.4 C.6 D.8
6.如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到的两个矩形都与原矩形相似,则原矩形长与宽的比是( )
A.2:1 B.1:2 C.3:2 D.2:1
7.函数y=kx(k≠0)与函数y=﹣kx+k在同一坐标系中的图象可能是( )
A. B. C. D.
8.某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据题意,列方程正确的是( )
A.150(1-x2)=96 B.150(1-x)=96 C.150(1-x)2=96 D.150(1-2x)=96
9.在一个不透明的口袋中,放置3个黄球,1个红球和n个黄球,这些球除了颜色其它都相同 ,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了蓝秋出现的频率,如图所示,则n的值是( )
A.4 B.5 C.6 D.8
(第9题图) (第10题图)
10.如图,正方形ABCD的顶点B在x轴上,点A,C在反比例函数y=kx图象上,若直线BC的函数表示式为y=12x-4,则反比例函数表达式为( )
A.y=6x B.y=12x C.y=16x D.y=24x
二.填空题。(每小题4分,共24分)
11.如图,AB∥CD∥EF,若AC=6,CE=3,DF=2,则BD的长为 .
(第11题图) (第14题图) (第15题图)
12.某医院需从A,B,C三名志愿者中任意抽调两人助力一项工作,恰好抽取B和C的概率是 。
13.若m是方程x2-x-1=0的一个根,则m2-m+2021的值为 .
14.如图,一次函数y1=k1x+b的图象与反比例函数y2=k2x的图象交于点A(1,m),B(4,n),当y1>y2时,x的取值范围是 .
15.如图,为了测量操场上一棵大树的高度,小明拿来一面镜子,平放在离树根部5m的地面上,然后沿着树根和镜子所在直线后退,当她后退1m时,正好镜中看到树的顶端,小明估计自己的眼睛到地面的距离为1.6m,则大树的高度是 m。
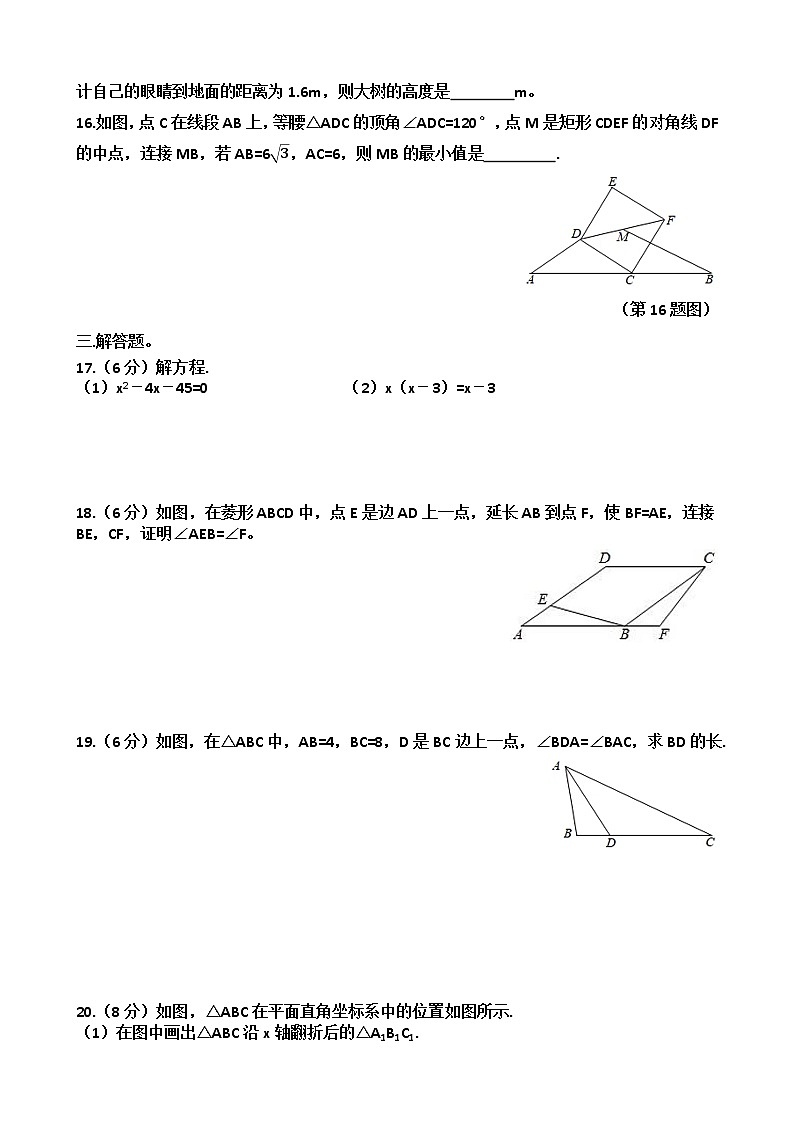
16.如图,点C在线段AB上,等腰△ADC的顶角∠ADC=120°,点M是矩形CDEF的对角线DF的中点,连接MB,若AB=63,AC=6,则MB的最小值是 .
(第16题图)
三.解答题。
17.(6分)解方程.
(1)x2-4x-45=0 (2)x(x-3)=x-3
18.(6分)如图,在菱形ABCD中,点E是边AD上一点,延长AB到点F,使BF=AE,连接BE,CF,证明∠AEB=∠F。
19.(6分)如图,在△ABC中,AB=4,BC=8,D是BC边上一点,∠BDA=∠BAC,求BD的长.
20.(8分)如图,△ABC在平面直角坐标系中的位置如图所示.
(1)在图中画出△ABC沿x轴翻折后的△A1B1C1.
(2)以点M(1,2)为位似中心,作出△A1B1C1按2:1放大后的位似图形△A2B2C2.
(3)填空:点A2坐标 ;△ABC和△A2B2C2的周长比是 .
21.(8分)目前,微信,支付宝,共享单车和网购给我们生活带来了很多便利,九(1)班学生对在校内你最认可的新生事物进行调查,随机调查了m人,(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如图所示的不完整的统计图.
(1)依据图中信息求出m= ,n= 。
(2)补全完整图形.
(3)根据调查结果,请估算全校1500名学生中,大约有多少人最认可微信和支付宝这两种新生事物?
22.(8分)一个不透明口袋中有三个小球,一个标有字母A,另外两个都标有字母B,除所标字母不同外,其它完全相同,小明和小刚做摸球游戏,小明从中随机摸出一个小球,记下字母后放回并搅匀,小刚再随机摸出一个小球,两次摸出的小球所标字母相同则小明赢,所标字母不同则小刚赢.
(1)用画树状图或列表的方法,求小明赢的概率.
(2)请问这个游戏规则对双方公平吗?说明理由.
23.(8分)如图,正方形ABCD中,AB=9,E是BC上一点,过E做EF⊥AE交CD于点F,连接AF.
(1)证明:△ABE∽△ECF.
(2)当BE=3时,求CF的长.
24.(10分)2020年,某家庭纯收入为2500元,通过政府产业扶持,发展养殖业,到2022年,家庭收入为3600元.
(1)求该家庭2022年到2022年人均收入的年平均增长率.
(2)若年平均增长率保持不变,2023年家庭年收入是否达到4200元?
25.(12分)如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=kx的图象交于A(n,4),B(2,2)两点.
(1)求反比例函数以及一次函数表达式。
(2)若点P是直线AB左侧x轴上一点,若△ABP的面积为1,求点P的坐标.
(3)过点A作直线,与第三象限的反比例函数图象交于另一点C,连接BC,当线段AC被y轴分成长度为1:2两部分时,求BC的长.
26.(12分)(1)如图1,△ABC中,∠BAC=90°,AB=AC,点D是BC上一点,连接AD,以AD为一边作△ADE,使∠DAE=90°,AD=AE,连接BE,BE,CD的数量关系是 ,位置关系是 .
(2)如图2,△ABC中,∠BAC=90°,AB=AC,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=ME,连接BE,求∠EBD度数.
(3)如图3,Rt△ABC中,∠BAC=90°,∠ACB=30°,BC=6,点M是AB中点,点D是BC上一点且BD=1,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=3ME,连接BE,求BE的长.
图1 图2 图3
答案解析
一.单选题。(每小题4分,共40分)
1.若ab=53,则a-bb的值为( B )
A.43 B.23 C.35 D.25
2.下列几何体中,其俯视图与主视图完全相同的是( C )
A. B. C. D.
3.若x=1是方程x2+mx+3=0的一个根,则方程的另一根是( A )
A.3 B.4 C.﹣3 D.﹣4
4.如图,矩形ABCD中,对角线AC,BD交于点O,添加下面一个条件,能使矩形ABCD为正方形的是( B )
A.BD=AB B.DC=AD C.∠AOB=60° D.OD=CD
(第4题图) (第5题图) (第6题图)
5.如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( B )
A.2 B.4 C.6 D.8
6.如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到的两个矩形都与原矩形相似,则原矩形长与宽的比是( D )
A.2:1 B.1:2 C.3:2 D.2:1
7.函数y=kx(k≠0)与函数y=﹣kx+k在同一坐标系中的图象可能是( C )
A. B. C. D.
8.某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据题意,列方程正确的是( C )
A.150(1-x2)=96 B.150(1-x)=96 C.150(1-x)2=96 D.150(1-2x)=96
9.在一个不透明的口袋中,放置3个黄球,1个红球和n个黄球,这些球除了颜色其它都相同 ,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了蓝秋出现的频率,如图所示,则n的值是( C )
A.4 B.5 C.6 D.8
(第9题图) (第10题图)
10.如图,正方形ABCD的顶点B在x轴上,点A,C在反比例函数y=kx图象上,若直线BC的函数表示式为y=12x-4,则反比例函数表达式为( D )
A.y=6x B.y=12x C.y=16x D.y=24x
二.填空题。(每小题4分,共24分)
11.如图,AB∥CD∥EF,若AC=6,CE=3,DF=2,则BD的长为 4 .
(第11题图) (第14题图) (第15题图)
12.某医院需从A,B,C三名志愿者中任意抽调两人助力一项工作,恰好抽取B和C的概率是 13 。
13.若m是方程x2-x-1=0的一个根,则m2-m+2021的值为 2022 .
14.如图,一次函数y1=k1x+b的图象与反比例函数y2=k2x的图象交于点A(1,m),B(4,n),当y1>y2时,x的取值范围是 x<0或1<x<4 .
15.如图,为了测量操场上一棵大树的高度,小明拿来一面镜子,平放在离树根部5m的地面上,然后沿着树根和镜子所在直线后退,当她后退1m时,正好镜中看到树的顶端,小明估计自己的眼睛到地面的距离为1.6m,则大树的高度是 8 m。
16.如图,点C在线段AB上,等腰△ADC的顶角∠ADC=120°,点M是矩形CDEF的对角线DF的中点,连接MB,若AB=63,AC=6,则MB的最小值是 9-23 .
(第16题图)
三.解答题。
17.(6分)解方程.
(1)x2-4x-45=0 (2)x(x-3)=x-3
解:(x-9)(x+5)=0 解:(x-1)(x-3)=0
x1=9,x2=﹣5 x1=1,x2=3
18.(6分)如图,在菱形ABCD中,点E是边AD上一点,延长AB到点F,使BF=AE,连接BE,CF,证明∠AEB=∠F。
证明:∵在菱形ABCD中
∴AD∥BC AB=BC
∴∠A=∠CBF
在△ABE和△BCF中
AE=BF∠A=∠CBFAB=BC
∴△ABE≌△BCF
∴∠AEB=∠F
19.(6分)如图,在△ABC中,AB=4,BC=8,D是BC边上一点,∠BDA=∠BAC,求BD的长.
解:∵∠BDA=∠BAC,∠B=∠B
∴△ABD∽△ABC
∴BDAB=ABBC
∵AB=4,BC=8
即BD4=48
∴BD=2
20.(8分)如图,△ABC在平面直角坐标系中的位置如图所示.
(1)在图中画出△ABC沿x轴翻折后的△A1B1C1.
(2)以点M(1,2)为位似中心,作出△A1B1C1按2:1放大后的位似图形△A2B2C2.
(3)填空:点A2坐标 ;△ABC和△A2B2C2的周长比是 .
(1)(2)
(3)(3,6) 1:2
21.(8分)目前,微信,支付宝,共享单车和网购给我们生活带来了很多便利,九(1)班学生对在校内你最认可的新生事物进行调查,随机调查了m人,(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如图所示的不完整的统计图.
(1)依据图中信息求出m= ,n= 。
(2)补全完整图形.
(3)根据调查结果,请估算全校1500名学生中,大约有多少人最认可微信和支付宝这两种新生事物?
(1)100 35
(2)略
(3)1800×40+35100=1350人
答:大约1350人
22.(8分)一个不透明口袋中有三个小球,一个标有字母A,另外两个都标有字母B,除所标字母不同外,其它完全相同,小明和小刚做摸球游戏,小明从中随机摸出一个小球,记下字母后放回并搅匀,小刚再随机摸出一个小球,两次摸出的小球所标字母相同则小明赢,所标字母不同则小刚赢.
(1)用画树状图或列表的方法,求小明赢的概率.
(2)请问这个游戏规则对双方公平吗?说明理由.
(1)
共有9种等可能性,其中两次摸出所标字母有5种,小明赢的概率P=59
(2)小明赢的可能性是P=59,小刚赢的概率是P=1-59=49
59>49
不公平
23.(8分)如图,正方形ABCD中,AB=9,E是BC上一点,过E做EF⊥AE交CD于点F,连接AF.
(1)证明:△ABE∽△ECF.
(2)当BE=3时,求CF的长.
(1)∵四边形ABCD是正方形
∴∠B=∠C=90°
∴∠BAE+∠AEB=90°
∵EF⊥AE
∴∠AEB+∠CEF=90°
∴∠BAE=∠CEF
∴△ABE∽△ECF
(2)∵△ABE∽△ECF
∴ABEC=BECF
∴96=3CF
∴CF=1
24.(10分)2020年,某家庭纯收入为2500元,通过政府产业扶持,发展养殖业,到2022年,家庭收入为3600元.
(1)求该家庭2022年到2022年人均收入的年平均增长率.
(2)若年平均增长率保持不变,2023年家庭年收入是否达到4200元?
(1)解设:平均增长率为x.
2500(1+x)2=3600
(1+x)2=3625
x1=20% x2=﹣2.2(舍去)
(2)3600×(1+20%)=4320元
4320>4200
能达到
25.(12分)如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=kx的图象交于A(n,4),B(2,2)两点.
(1)求反比例函数以及一次函数表达式。
(2)若点P是直线AB左侧x轴上一点,若△ABP的面积为1,求点P的坐标.
(3)过点A作直线,与第三象限的反比例函数图象交于另一点C,连接BC,当线段AC被y轴分成长度为1:2两部分时,求BC的长.
(1)将B(2,2)代入y=kx得
k=2×2=4
将A(n,4)代入反比例函数y=4x
n=1,
将A(1,4),B(2,2)代入y=ax+b
k+b=42k+b=2 解得k=﹣2b=6
y=﹣2x+6
(2)解设P(m,0)
△ABP的面积=(3-m)×4÷2-(3-m)×2÷2=1
m=2
P(2,0)
(3)设直线AC交y轴于点I,如图分别过点A,C作y轴的垂线,垂足分别为H,K,则AH∥CK.
∴△AHI∽△CKI
∴AHCK=AICI
当AI:CI=1:2时,AH:CK=1:2,又AH=1,
∴CK=2,
∴xC=﹣2
将xC=﹣2代入y=4x
得到y=﹣2
∴C(﹣2,﹣2)
∴BC=42
当CI:AI1:2时,C(﹣12,﹣8)
∴BC=5172
26.(12分)(1)如图1,△ABC中,∠BAC=90°,AB=AC,点D是BC上一点,连接AD,以AD为一边作△ADE,使∠DAE=90°,AD=AE,连接BE,BE,CD的数量关系是 ,位置关系是 .
(2)如图2,△ABC中,∠BAC=90°,AB=AC,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=ME,连接BE,求∠EBD度数.
(3)如图3,Rt△ABC中,∠BAC=90°,∠ACB=30°,BC=6,点M是AB中点,点D是BC上一点且BD=1,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=3ME,连接BE,求BE的长.
图1 图2 图3
(1)BE=CD BE⊥CD
(2)如图,过点A作AG∥MD交BC于点G,△BDM∽△BGA
∴DMAG=BMAB
过点A作AF∥ME交BE的延长线于点F,则△BME∽△BAF
∴EMAF=BMAB
∴DMAG=EMAF
∵MD=ME
∴AF=AG
∵AG∥DM
∴∠BMD=∠BAG
∵ME∥AF
∴∠BME=∠BAF
∴∠FAG=90°
在Rt△ABC中,AB=AC
∴∠ABC=∠C=45°
∴∠ABF=∠C=45°
∴∠EBD=∠ABF+∠ABC=90°
(3)3
2022-2023学年山东省济南市历城区九年级上学期数学期中试题及答案: 这是一份2022-2023学年山东省济南市历城区九年级上学期数学期中试题及答案,共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济南市历城区九年级上学期数学12月月考试题及答案: 这是一份2022-2023学年山东省济南市历城区九年级上学期数学12月月考试题及答案,共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济南市槐荫区九年级上学期数学期中试题及答案: 这是一份2022-2023学年山东省济南市槐荫区九年级上学期数学期中试题及答案,共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












