广东省深圳市福田外国语学校2022-2023学年九年级上学期期中数学试卷(含答案)

2022-2023学年广东省深圳市福田外国语学校九年级（上）期中数学试卷

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 某零件由两长方体组合而成如图所示，则它的左视图是(    )

A.
B.
C.
D.

2. 下列方程中，关于的一元二次方程的是(    )

A.  B.  C.  D.

3. 已知四边形是平行四边形，下列结论中错误的是(    )

A. 当时，它是矩形 B. 当时，它是菱形
C. 当时，它是菱形 D. 当时，它是正方形

4. 在一个不透明的纸箱中，共有个蓝色、红色的玻璃球，它们除颜色外其他完全相同．小柯每次摸出一个球后放回，通过多次摸球试验后发现摸到蓝色球的频率稳定在，则纸箱中红色球很可能有(    )

A. 个 B. 个 C. 个 D. 个

5. 若关于的一元二次方程有两个不相等的实数根，则的取值范围是(    )

A.  B. 且 C.  D.

6. 对于反比例函数，下列说法正确的是(    )

A. 图象经过点 B. 图象位于第一、三象限
C. 当时，随的增大而减小 D. 当时，随的增大而增大

7. 如图．在宽为，长为的矩形地面上修建两条宽均为的小路阴影，余下部分作为草地，草地面积为，根据图中数据，求得小路宽的值为(    )

A.  B.
C.  D.

8. 如图，在中，点在上，，交于点，则下列结论正确的是(    )

A.  B.
C.  D.

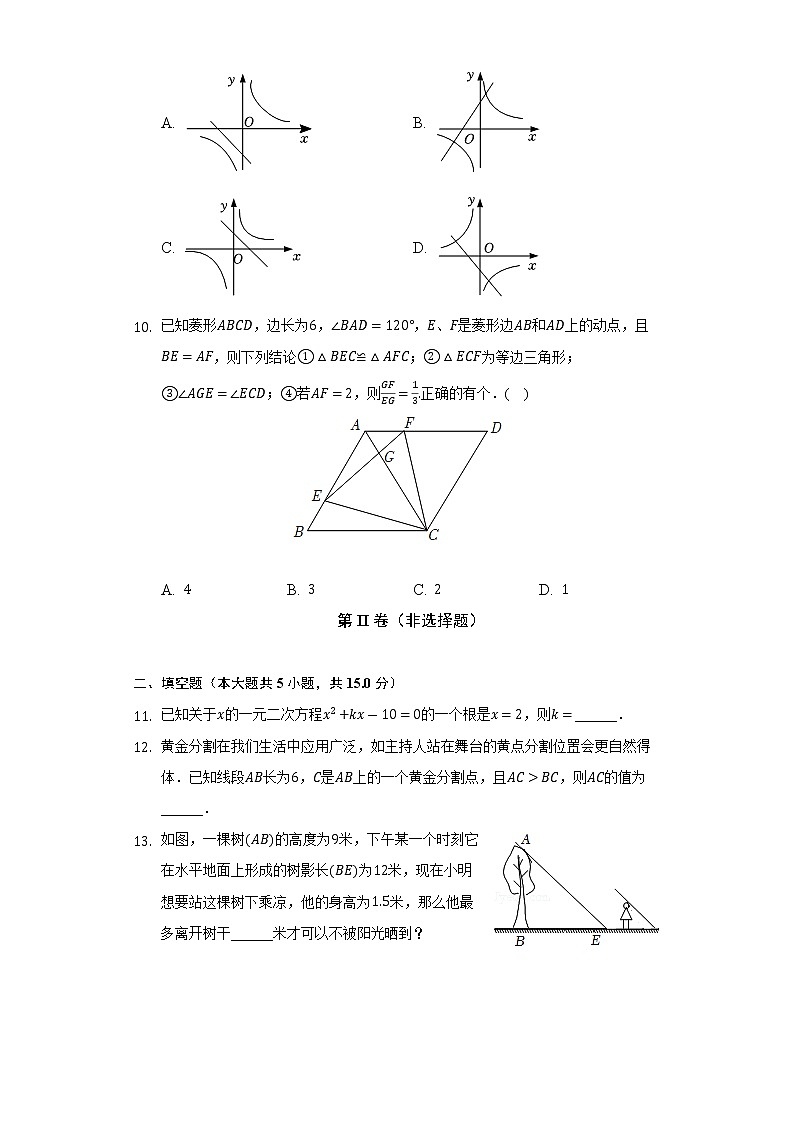
9. 函数和在同一平面直角坐标系中的大致图象可能是(    )

A.  B.
C.  D.

10. 已知菱形，边长为，，、是菱形边和上的动点，且，则下列结论≌；为等边三角形；；若，则正确的有个．(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共5小题，共15.0分）

11. 已知关于的一元二次方程的一个根是，则______．
12. 黄金分割在我们生活中应用广泛，如主持人站在舞台的黄点分割位置会更自然得体．已知线段长为，是上的一个黄金分割点，且，则的值为______．
13. 如图，一棵树的高度为米，下午某一个时刻它在水平地面上形成的树影长为米，现在小明想要站这棵树下乘凉，他的身高为米，那么他最多离开树干______米才可以不被阳光晒到？

14. 如图，在平面直角坐标系中，反比例函数的图象和矩形在第一象限，平行于轴，且，，点的坐标为将矩形向下平移，若矩形的两个顶点恰好同时落在反比例函数的图象上，则矩形的平移距离的值为______．

15. 如图，在中，，以，为边分别向外作正方形和正方形，交于点，交于点若，则的值为______．

三、解答题（本大题共7小题，共55.0分。解答应写出文字说明，证明过程或演算步骤）

16. 本小题分
    解方程：
    ；
    ．
17. 本小题分
    如图，在平面直角坐标系中，的三个顶点坐标分别为，，．
    画出关于轴对称的图形；
    以原点为位似中心，位似比为：，在轴的左侧，画出放大后的图形．
    填空：直接写出点的坐标______；与的周长比是______．

18. 本小题分
    “双减”政策的实施，不仅减轻了学生的负担，也减轻了家长的负担，回归了教育的初衷．现学校计划在某个班向家长展示“双减”背景下的课堂教学活动，用于展开活动的备选班级有个为七年级班级，个为八年级班级．
    选中八年级班级来展示的概率为______．
    由于报名参加观摩课堂教学活动的家长较多，学校决定在两个班同时开展活动，请用树状图或列表法求选中的既有七年级又有八年级的概率．
19. 本小题分
    年北京冬季奥运会于月日至月日在北京市和河北省张家口市联合举行，冬奥会吉祥物为“冰墩墩”．
    据市场调研发现，某工厂今年二月份共生产个“冰墩墩”，为增大生产量，该工厂平均每月生产量增加，经过两个月后，则该工厂在四月份能生产多少个“冰墩墩”？
    已知某商店“冰墩墩”平均每天可销售个，每个盈利元，在每个降价幅度不超过元的情况下，每下降元，则每天可多售件，如果每天要盈利元，则每个“冰墩墩”应降价多少元？

20. 本小题分
    小亮在学习了反比例函数的图象和性质后，进一步研究了函数的图象与性质．他利用描点法在给出的平面直角坐标系中画出函数的图象的一部分，并解答下列问题．

______，______，并在图中补全函数的图象．
根据以上探究结果，完成下列问题：
函数，自变量的取值范围为______；
函数的图象是______图形填中心对称或轴对称；
直接写出当时，自变量的值______．
求出当一次函数与函数图象交点个数不少于两个时，的取值范围是______．
 

21. 本小题分
    如图，在矩形中，，点，分别在边，上均不与端点重合，且，以和为邻边作矩形，连接，．
    
    【问题发现】
    如图，当时，与的数量关系为______，与的数量关系为______．
    【类比探究】
    如图，当时，矩形绕点顺时针旋转，连接，则与之间的数量关系是否发生变化？若不变，请就图给出证明：若变化，请写出数量关系，并就图说明理由．
    【拓展延伸】
    在的条件下，已知，，当矩形旋转至，，三点共线时，请直接写出线段的长．
22. 本小题分
    【基础巩固】如图，在中，，，是边上一点，是边上一点，求证：；
    【尝试应用】如图，在四边形中，点是边的中点，，若，，求线段的长．
    【拓展提高】在中．，，以为直角顶点作等腰直角三角形，点在上，点在上．若，求的长．
    
    

答案和解析

1.【答案】 

【解析】解：从左面看，视图是一个矩形，由于物体正面看有上下两层，从左边看不到凹槽的棱，用虚线表示，
故选：．
找到从左面看所得到的图形即可，注意所有的看到的或看不到的棱都应表现在左视图中，看得见的用实线，看不见的用虚线，虚实重合用实线．
本题考查了三视图的知识，左视图是从物体的左面看得到的视图．
 

2.【答案】 

【解析】解：是分式方程，不是整式方程，不是一元二次方程，故本选项不符合题意；
B.是一元三次方程，不是一元二次方程，故本选项不符合题意；
C.是一元二次方程，故本选项符合题意；
D.是二元二次方程，不是一元二次方程，故本选项不符合题意；
故选：．
根据一元二次方程的定义逐个判断即可．
本题考查了一元二次方程的定义，能熟记一元二次方程的定义是解此题的关键，注意：只含有一元未知数，并且所含未知数的项的最高次数是的整式方程，叫一元二次方程．
 

3.【答案】 

【解析】解：、四边形是平行四边形，
又，
四边形是矩形，故本选项不符合题意；
B、四边形是平行四边形，
又，
四边形是菱形，故本选项不符合题意；
C、四边形是平行四边形，
又，
四边形是菱形，故本选项不符合题意；
D、四边形是平行四边形，
又，
四边形是矩形，不一定是正方形，故本选项符合题意；
故选：．
根据矩形、菱形、正方形的判定逐个判断即可．
本题考查了对矩形的判定、菱形的判定，正方形的判定的应用，能正确运用判定定理进行判断是解此题的关键，难度适中．
 

4.【答案】 

【解析】解：，
故选：．
根据篮球的频率得出概率，再根据概率计算得出结论即可．
本题主要考查利用频率估计概率的知识，根据题意得出红球的概率是解题的关键．
 

5.【答案】 

【解析】解：根据题意得且，
解得且．
故选：．
根据一元二次方程的定义和判别式的意义得到且，然后求出两不等式的公共部分即可．
本题考查了根的判别式：一元二次方程的根与有如下关系：当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程无实数根．
 

6.【答案】 

【解析】解：、，点不满足关系式，因此选项不符合题意；
B、；
它的图象在第二、四象限，因此选项不符合题意；
C、；
它的图象在第二、四象限，当时，随的增大而增大，因此选项不符合题意；
D、；
它的图象在第二、四象限，当时，随的增大而增大，因此选项符合题意．
故选：．
根据反比例函数的性质对各选项进行逐一分析即可．
本题主要考查了反比例函数的图象和性质，熟练掌握反比例函数的性质是解题的关键．
 

7.【答案】 

【解析】解：剩余部分可合成长为，宽为的矩形，
根据题意得：，
故选：．
剩余部分可合成长为，宽为的矩形，利用矩形的面积公式结合草地面积为，即可得出关于的一元二次方程．
本题考查了一元二次方程的应用，解题的关键是读懂题意，找到等量关系，列出方程．
 

8.【答案】 

【解析】解：，，
，
，
∽，
，
，，
，
的值无法求解，
故选：．
由，可得出，由可得出∽，再利用相似三角形的性质即可得解．
此题考查了相似三角形的判定与性质，熟记相似三角形的判定与性质是解题的关键．
 

9.【答案】 

【解析】解：在函数和中，
当时，函数的图象经过第一、三象限，函数的图象经过第一、二、四象限，故选项A、B错误，选项C正确，
当时，函数的图象经过第二、四象限，函数的图象经过第一、二、三象限，故选项D错误，
故选：．
根据题目中函数的解析式，利用一次函数和反比例函数图象的特点解答本题．
本题考查反比例函数的图象、一次函数的图象，解答本题的关键是明确题意，利用分类讨论的数学思想解答．
 

10.【答案】 

【解析】解：四边形是菱形，
，，
，
，
和都是等边三角形，
，，
，
≌，故正确；
≌，
，，
，
，
是等边三角形，故正确；
；
，
，故错误；
过点作交于点，

，，
是等边三角形，
，
≌，
，
，
，
，
∽，
，故错误，
正确个数为个，
故选：．
由证明≌，正确；由全等三角形的形状得，，再由，得，得是等边三角形，正确；由，，得，故正确；过点作交下点点，易证是等边三角形，则，由，则∽，得正确，
本题考查了菱形的性质、等边三角形性质、全等三角形的判定与性质、相似三角形的判定与性质等知识；熟练掌握菱形的性质、全等三角形的判定与性质、相似三角形的判定与性质是解题的关键．
 

11.【答案】 

【解析】解：关于的一元二次方程的一个根是，
，
解得，
故答案为：．
把代入方程得出，再求出方程的解即可．
本题考查了解一元二次方程，一元二次方程的解和解一元一次方程等知识点，能熟记一元二次方程的解的定义是解此题的关键，注意：解一元二次方程的方法有：直接开平方法，公式法，配方法，因式分解法等．
 

12.【答案】 

【解析】解：为的一个黄金分割点，，且，
，
故答案为：．
由黄金分割的定义得，即可得出结论．
本题考查的是黄金分割的概念，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，比值叫做黄金比．
 

13.【答案】 

【解析】解：设小明这个时刻在水平地面上形成的影长为米，
根据题意，得，
解得，
小明这个时刻在水平地面上形成的影长为米，
因为米，
所以他最多离开树干米才可以不被阳光晒到．
故答案为：．
设小明这个时刻在水平地面上形成的影长为米，利用同一时刻物体的高度与影长成正比得到，解得，然后计算两影长的差即可．
本题考查了相似三角形的应用和平行投影．由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影．同一时刻物体的高度与影长成正比．
 

14.【答案】 

【解析】解：四边形是矩形，平行于轴，且，，点的坐标为，
，，
，，
矩形平移后的坐标是，的坐标是，
、落在反比例函数的图象上，
，
解得，
故答案为：．
根据矩形性质得出，，即可得出点的坐标，则矩形平移后的坐标是，的坐标是，得出，求出即可．
本题考查了矩形性质，用待定系数法求反比例函数的解析式，平移的性质的应用，主要考查学生的计算能力．
 

15.【答案】 

【解析】解：如图，过点作，交的延长线于点，交的延长线于点，

，
∽，
，
设，，
，，
，，
，
，
在和中，
，
≌，
，，
，
∽，
，
，，
，
，
∽，
，
设，，
，
，
，，
，
故答案为：
设，，由“”可证≌，可得，，利用相似三角形的性质分别求出，的长，即可求解．
本题考查了相似三角形的判定和性质，正方形的性质，全等三角形的判定和性质，添加恰当辅助线构造相似三角形是解题的关键．
 

16.【答案】解：，
，
，
或，
解得，；
，
，，，
，
，
，． 

【解析】提公因式法因式分解解方程即可；
利用公式法解方程即可；
本题考查一元二次方程因式分解法以及一元二次方程公式法，解题的关键是掌握提公因式法分解因式以及熟记求根公式．
 

17.【答案】  ： 

【解析】解：如图，为所作；
如图，为所作；

点的坐标为；与的周长比是：．
故答案为：；：．
利用关于轴对称的点的坐标特征点、、的坐标，然后描点即可；
把点、、的横纵坐标都乘以得到点、、的坐标，然后描点即可；
由得到点的坐标，然后根据位似的性质得到与的周长比．
本题考查了作图位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为，那么位似图形对应点的坐标的比等于或也考查了轴对称变换．
 

18.【答案】 

【解析】解：选中八年级班级来展示的概率为，
故答案为：；
画树状图：

共有种等可能结果，其中选中的既有七年级又有八年级的结果数为，
所以选中的既有七年级又有八年级的概率为．
直接根据概率公式求解即可；
画树状图展示所有种等可能结果，再找出选中的既有七年级又有八年级的结果数，然后根据概率公式计算．
本题考查列表法与树状图法，解题时要注意此题是放回实验还是不放回实验．注意：概率所求情况数总情况数．
 

19.【答案】解：个．
答：该工厂在四月份能生产个“冰墩墩”．
设每个“冰墩墩”降价元，则每个盈利元，平均每天可售出个，
依题意得：，
整理得：，
解得：，不符合题意，舍去，
答：每个“冰墩墩”应降价元． 

【解析】利用该工厂在四月份生产“冰墩墩”的数量该工厂在二月份生产“冰墩墩”的数量，即可求出结论；
设每个“冰墩墩”降价元，则每个盈利元，平均每天可售出个，利用该商店每天销售“冰墩墩”获得的利润每个的销售利润平均每天的销售量，即可得出关于的一元二次方程，解之取其符合题意的值即可得出结论．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
 

20.【答案】      轴对称 或   

【解析】解：把，代入得，把代入得，
，．
故答案为：，．
画出函数的图象如图所示，
；

观察函数图象，
函数，自变量的取值范围为；
函数的图象是轴对称图形填中心对称或轴对称；
当时，自变量的值是或
故答案为：，轴对称，或．

如图，

当直线过时，函数的图象与函数的图象有两个交点，此时，
由图象可知，当时，函数的图象与函数的图象交点个数不少于两个，
故答案为：．
利用函数解析式分别求出对应的函数值，利用描点法画出图象即可．
观察图象即可得到结论．
利用图象即可解决问题．
本题是反比例函数与一次函数的交点问题，考查反比例函数的图象与性质，数形结合是解题的关键．
 

21.【答案】   

【解析】解：当时，，，
，
，
四边形和四边形都是矩形，且，，
四边形和四边形都是正方形，
，，，
，，
，
、、三点在同一条直线上，
，，
，，
，
故答案为：，．
发生变化，，
理由：如图，连接，当时，则，，
，
，
，
∽，
，，
，，
，
∽，
，
，
．
，，
，，，
，
如图，，，三点共线，且点在线段上，
，
，
；
如图，，，三点共线，且点在线段的延长线上，
，
，
，
综上所述，线段的长是或．
当时，，，则，所以，再证明、、三点在同一条直线上，由勾股定理得，，
所以，于是得到问题的答案；
先证明∽，得，，则，，即可证明∽，再根据勾股定理求得，则，所以；
分两种情况，一是，，三点共线，且点在线段上，由勾股定理求得，则；二是，，三点共线，且点在线段的延长线上，由勾股定理求得，则．
此题重点考查矩形的性质、正方形的性质、旋转的性质、相似三角形的判定与性质、勾股定理、数形结合与分类讨论数学思想的运用等知识与方法，此题综合性强，难度较大，正确地作出所需要的辅助线是解题的关键．
 

22.【答案】证明：，，
，
，，
，
∽，
，
；

解：如图中，延长交的延长线于点．

，
，，
，
，
∽，
，
，
，
，
，
，
，，
；

解：如图，过点作与交于点，使，

，
，
∽，
，
，，
，
，，
，
∽，
，
，
，
，
，
． 

【解析】利用一线三等角模型，可说明∽，得；
如图中，延长交的延长线于点证明∽，推出，求出，，再利用勾股定理求解；
过点作与交于点，使，由同理得∽，可知，再利用∽，可得答案；
本题是相似形综合题，相似三角形的判定与性质，等腰三角形的性质，熟练掌握一线三等角基本几何模型是解题的关键．