

山东省滨州市滨城区2022-2023学年九年级上学期期中数学试题(含答案)
展开2022-2023学年九年级第一学期教学质量检测
九年级数学试题(A)
温馨提示:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。满分120分。考试用时120分钟。
2.答卷前,考生务必用0.5毫米黑色签字笔将自己的学校、姓名、准考证号填写在答题卡中规定的位置上。
3.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
4.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第Ⅰ卷(选择题共36分)
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑。每小题涂对得3分,满分36分.
1.下列是一元二次方程的是( )
A. B.
C. D.
2.下表是代数式的值的情况,根据表格中的数据,可知方程的根是( )
… | 0 | 1 | 2 | 3 | 4 | … | ||||
… | 12 | 6 | 2 | 0 | 0 | 2 | 6 | 12 | … |
A., B.,
C., D.,
3.用配方法解一元二次方程,配方正确的是( )
A. B. C. D.
4.将二次函数向左平移5个单位,再向上平移3个单位,所得新抛物线表达式为( )
A. B.
C. D.
5.当时,一元二次方程的求根公式是( )
A. B.
C. D.
6.二次函数的图象与x轴交点的情况是( )
A.没有交点 B.有一个交点 C.有两个交点 D.与m的值有关
7.平面直角坐标系中,O为坐标原点,点A的坐标为,将OA绕原点按逆时针方向旋转90°得OB,则点B的坐标为( )
A. B. C. D.
8.随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是6000元,现在生产一吨药的成本是3600元.下面所列方程正确的是( )
A.设生产成本的年平均下降率为x,
B.设生产成本的年下降率为x,
C.设生产成本的年下降率为x,
D.设生产成本的年平均下降率为x,
9.已知实数x,y满足,则的最大值为( )
A.1 B.2 C.3 D.4
10.根据表中二次函数的自变量x与函数值y的对应值,判断一元二次方程的一个根x的取值范围是( )
x | 6.17 | 6.18 | 6.19 | 6.20 |
y | 0.02 | 0.04 |
A. B.
C. D.
11.已知点,在二次函数的图象上,则下列说法正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
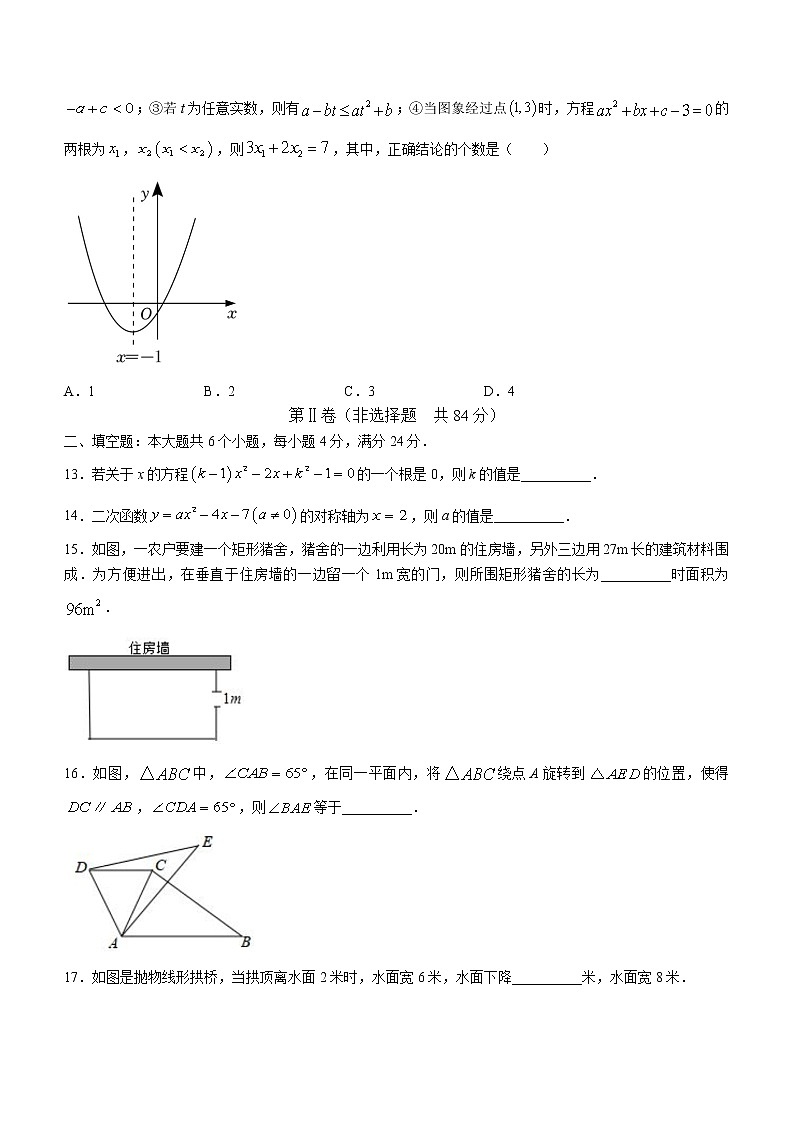
12.己知二次函数的部分图象如图所示,对称轴为直线,有以下结论:①;②;③若t为任意实数,则有;④当图象经过点时,方程的两根为,,则,其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题 共84分)
二、填空题:本大题共6个小题,每小题4分,满分24分.
13.若关于x的方程的一个根是0,则k的值是__________.
14.二次函数的对称轴为,则a的值是__________.
15.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为20m的住房墙,另外三边用27m长的建筑材料围成.为方便进出,在垂直于住房墙的一边留一个1m宽的门,则所围矩形猪舍的长为__________时面积为.
16.如图,中,,在同一平面内,将绕点A旋转到的位置,使得,,则等于__________.
17.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降__________米,水面宽8米.
18.如图,点P是正内一点.,,,将线段AP绕点A逆时针旋转60°得到线段,连结.,,下列结论中正确的是__________(填序号)
①可以由绕点A逆时针旋转60°得到;
②线段;
③四边形的面积为;
④.
三、解答题:本大题共6个小题,满分60分.解答时请写出必要的演推过程.
19.(12分)解一元二次方程:
(1); (2)
(3); (4)(利用配方法).
20.(6分)如图,正方形网格中,每个小方格都是边长为1的正方形,的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题
(1)△ABC的面积为__________;
(2)将△ABC向上平移5个单位长度,画出平移后的;
(3)以坐标原点O为对称中心,画出与成中心对称的图形.
21.(8分)关于的一元二次方程有两个不相等的实数根,
(1)求m的取值范围;
(2)若方程有一个根为,求m的值和另一根.
22.(10分)某饮料批发商店平均每天可售出某款饮料300瓶,售出1瓶该款饮料的利润是1元.经调查发现,若该款饮料的批发价每降低0.1元,则每天可多售出100瓶.为了使每天获得的利润更多,该饮料批发商店决定降价x元.
(1)当x为多少时,该饮料批发商店每天卖出该款饮料的利润为400元?
(2)当饮料批发商店决定降价为多少元时,每天卖出该款饮料的利润(元)最大,最大利润是多少?
23.(12分)某公园要修建一个圆形喷水池,在池中心竖直安装一根水管,水管OA长2.25m.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m.
(1)建立如图所示平面直角坐标系,求抛物线(第一象限部分)的解析式;
(2)不考虑其它因素,水池的直径至少要多少米才能使喷出的水流不落到池外?
(3)实际施工时,经测量,水池的最大半径只有2.5m,在不改变喷出的抛物线形水柱形状的情况下,且喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,需对水管的长度进行调整,求调整后水管的最大长度.
24.(12分)如图,抛物线.与x轴交于A,B两点,与y轴交于C(0,3),直线经过点A且与抛物线交于另一点D.
(1)求抛物线的解析式;
(2)若P是位于直线AD上方的抛物线上的一个动点,连接PA,PD,求的面积的最大值;
(3)在第(2)问的条件下,求点P到直线AD的最大值.
2022-2023学年九年级第一学期期中考试答案
九年级数学试题(A)
参考答案与试题解析
一、选择题(共12小题,满分36分,每小题3分)
1.A 2.D 3.A 4.B 5.A 6.C 7.B 8.A 9.D 10.C 11.B 12.B
二、填空题(共6小题,满分24分,每小题4分)
13.±1;14.1;15.12或16;16.50°;17.;18.①②③
三、解答题:本大题共6个小题,满分60分.解答时请写出必要的演推过程.
19.解一元二次方程(每题3分):
解:(1)∵,,,
∴,
则,
即,;
(2)∵,
∴,,,
∴
则,
即,;
(3)∵,
∴,
则,
∴或,
解得,;
(4)∵,
∴,
则,
∴,即,
∴,
∴,.
20.解:(1)的面积为.(2分)
(2)如图,即为所求.(2分)
(3)如图,即为所求.(2分)
21.(1)∵方程有两个不相等的实数根,
∴
解得,;(4分)
(2)∵方程有一个根为,
∴,
解得,,
则,
解得,,,
答:m的值是,另一根是0.(8分)
22.解:(1)∵该饮料批发商店决定降价x元,
∴售出1瓶该款饮料的利润是元,平均每天可售出瓶.
依题意得:,(3分)
整理得:,
解得:,.
答:当x为0.2或0.5时,该饮料批发商店每天卖出该款饮料的利润为400.(5分)
(2)设饮料批发商店每天卖出该款饮料的利润为w元,理由如下:
依题意得
(7分)
当时,w的最大值为422.5元.(9分)
即该饮料批发商每天卖出该款饮料的利润的最大值为422.5元.(10分)
23.解:(1)由题意可知,抛物线的顶点坐标为(1,3),
∴设抛物线的解析式为:,
将(0,2.25)代入得,,
解得,
∴抛物线的解析式为:.(3分)
(2)令,得,,
解得(舍)或,
∵(米),
∴水池的直径至少要6米才能使喷出的水流不落到池外.(7分)
(3)将抛物线向下平移,使平移后的抛物线经过点(2.5,0),
设平移后的抛物线的解析式为:,
将(2.5,0)代入得,,
解得,
当时,.
∴调整后水管的最大长度米.(12分)
24.解:(1)∵直线经过点A,
∴令,则,
∴,
∴,
将,C(0,3)代入得:
,
解得:,
∴抛物线的解析式为:;(3分)
(2),
解得:,,
∴,
过点P作轴,交AD于E,
设,则,
∴,
△PAD的面积,
当时,的面积最大,且最大值是.(8分)
(3)∵,,根据勾股定理得:
设点P到AD的距离为h,
由第(2)问知:
点P到直线AD距离的最大值为(12分)
山东省滨州市滨城区2023—-2024学年八年级下学期4月期中数学试题: 这是一份山东省滨州市滨城区2023—-2024学年八年级下学期4月期中数学试题,共4页。
山东省滨州市滨城区2023-2024学年八年级上学期1月期末数学试题: 这是一份山东省滨州市滨城区2023-2024学年八年级上学期1月期末数学试题,共2页。
山东省滨州市滨城区2022-2023学年八年级上学期期末数学试题(含答案): 这是一份山东省滨州市滨城区2022-2023学年八年级上学期期末数学试题(含答案),共25页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












