【考点全掌握】人教版数学八年级上册-第3课时-乘法公式-同步考点（知识清单+例题讲解+课后练习）

第三课时——乘法公式

知识点一：平方差公式：

1. 公式内容：

  两数的和乘以两数的差等于这两数的          。

  即：          。

2. 特点分析：

  式子左边是两个二项式相乘，它们其中一项         ，另一项               。

  式子右边等于           的平方减去             的平方。

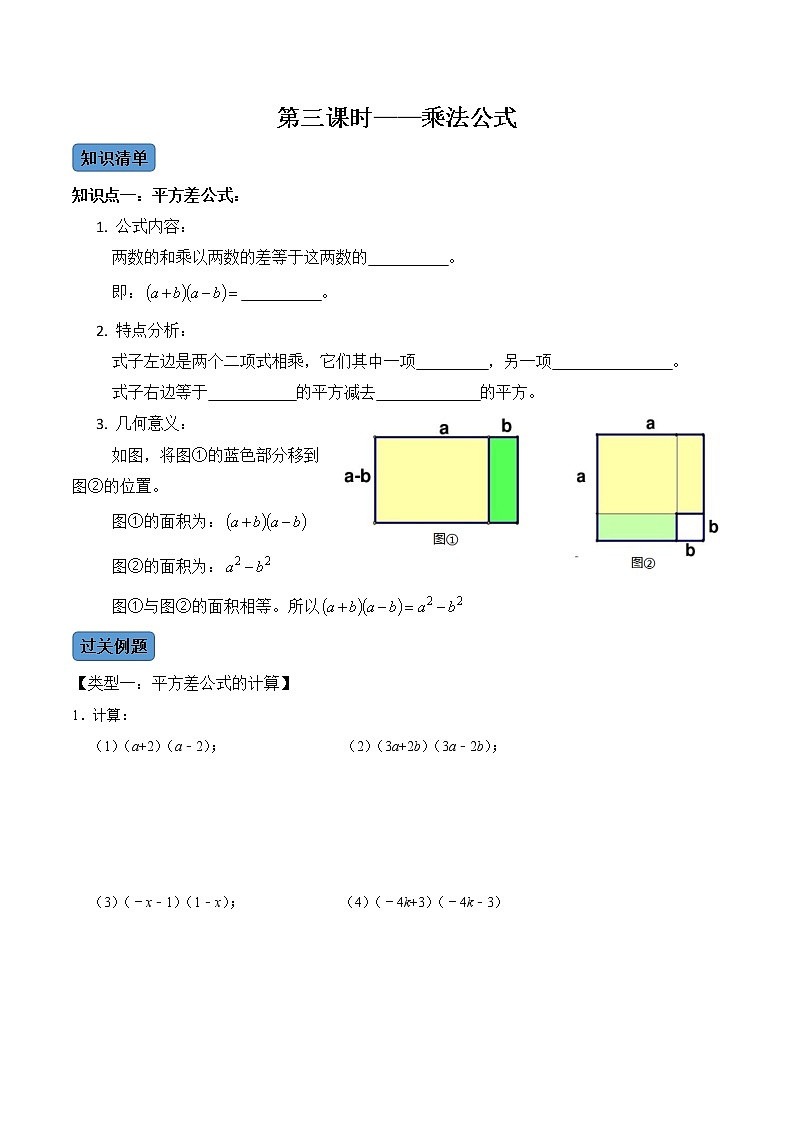
3. 几何意义：

  如图，将图①的蓝色部分移到

图②的位置。

     图①的面积为：

     图②的面积为：

     图①与图②的面积相等。所以

【类型一：平方差公式的计算】

1．计算：

（1）（a+2）（a﹣2）；                 （2）（3a+2b）（3a﹣2b）；

（3）（﹣x﹣1）（1﹣x）；              （4）（﹣4k+3）（﹣4k﹣3）

2．计算：

（1）（2m+3n）（2m﹣3n）；       （2）（﹣3a﹣b）（﹣3a+b）；

（3）（﹣4x+y）（y+4x）；         （4）（x+y）（x﹣y）+（y﹣z）（y+z）﹣（x+z）（x﹣z）．

【类型二：利用平方差公式求相关式子的值】

3．已知a+b＝﹣3，a﹣b＝1，则a2﹣b2的值是（　　）

A．8 B．3 C．﹣3 D．10

4．若a+b＝3，则a2﹣b2+6b的值为（　　）

A．3 B．6 C．9 D．12

5．若a2﹣b2＝，a+b＝，则a﹣b的值为（　　）

A．﹣ B． C． D．2

6．若x+y＝2，x2﹣y2＝4，则x﹣y的值为（　　）

A．1 B．2 C．3

【类型三：利用平方差公式简便运算】

7．计算：199×201＝（　　）

A．3999 B．4179 C．41790 D．39999

8．计算20202﹣2019×2021的结果是（　　）

A．﹣1 B．0 C．1 D．﹣2

9．化简（2+1）（22+1）（24+1）（28+1）（216+1）的结果是（　　）

A．232﹣1 B．232+1 C．（216+1）2 D．（216﹣1）2

【类型四：平方差公式的几何背景】

10．如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个长方形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（　　）

A．（a﹣b）2＝a2﹣2ab+b2 B．（a+b）2＝a2+2ab+b2 

C．a2﹣b2＝（a+b）（a﹣b） D．a2+ab＝a（a+b）

11．如图在边长为a的正方形纸片中剪去一个边长为b的小正方形，把余下的部分沿虚线剪开，拼成一个矩形，分别计算这两个图形阴影部分的面积，可以验证的等式是（　　）

A．a2﹣b2＝（a+b）（a﹣b） B．（a﹣b）2＝a2﹣2ab+b2 

C．（a+b）2＝a2+2ab+b2 D．a2+ab＝a（a+b）

12．【探究】如图1，边长为a的大正方形中有一个边长为b的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示），通过观察比较图2与图1中的阴影部分面积，可以得到乘法公式　               　．（用含a，b的等式表示）

【应用】请应用这个公式完成下列各题：

（1）已知4m2＝12+n2，2m+n＝4，则2m﹣n的值为　    　．

（2）计算：20192﹣2020×2018．

【拓展】

计算：1002﹣992+982﹣972+…+42﹣32+22﹣12．

知识点一：完全平方公式：

1. 公式内容：

  两数和（或差）的平方等于这两数的平方和加（或减）这两数的积的2倍。

  即：                  。

  其中              叫做完全平方和公式。                 叫做

完全平方差公式。

2. 特点分析

  式子左边是一个          平方。前项称为         ，后项称为        。

  式子右边等于            加上            ，首尾两项乘积的        放在平方两项

的中央。

      巧记：首平方加尾平方，首尾两倍放中央。

      提别提示：注意每一项包含前面的符号。

3. 几何意义：

  图1中面积的整体表示为：

      用各部分面积之和表示为：

      所以

      用同样的方法表示图2的面积即可得到。

4. 完全平方和公式与完全平方差公式的转化：

  ，

  ∵

  ∴

【类型一：完全平方公式的计算】

13．运用完全平方公式计算：

（1）（﹣2a+3）2；                  （2）（﹣3x+）2，

（4）（﹣x2﹣4y）2；                 （4）（1﹣2b）2．

14．计算：

（1）（2m+3）2；                      （2）（﹣1.3a+2b）2；

（3）（﹣2p﹣7q）2；                   （4）（a﹣b）2．

【类型二：利用完全平方公式变形求式子的值】

15．已知x﹣＝4，则x2+的值为（　　）

A．6 B．16 C．14 D．18

16．已知a2+b2＝8，a﹣b＝3，则ab的值为（　　）

A． B．3 C．﹣ D．5

17．已知x y＝9，x﹣y＝﹣3，则x2+3xy+y2的值为（　　）

A．27 B．9 C．54 D．18

18．已知（a+b）2＝5，（a﹣b）2＝3，求下列式子的值：

（1）a2+b2；                      （2）6ab．

19．已知a+b＝3，ab＝﹣4，求下列各式的值．

（1）（a﹣b）2；                   （2）a2﹣5ab+b2．

【类型三：完全平方公式的几何背景】

20．如图所示分割正方形，各图形面积之间的关系，验证了一个等式，这个等式是（　　）

       第20题                                      第21题

A．（y+x）2＝y2+xy+x2 B．（y+x）2＝y2+2xy+x2 

C．（y+x）（y﹣x）＝y2﹣x2 D．（y+x）2﹣（y﹣x）2＝4xy

21．有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为3和16，则正方形A，B的面积之和为（　　）

A．13 B．11 C．19 D．21

22．图1，是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图2的形状拼成一个正方形．

（1）图2中的阴影部分的面积为 　         　；

（2）观察图2，三个代数式（m+n）2，（m﹣n）2，m n之间的等量关系是 　                         　；

（3）若x+y＝﹣6，x y＝2.75，求x﹣y；

（4）观察图3，你能得到怎样的代数恒等式呢？

知识点一：平方差公式与完全平方公式的推广：

1. 平方差公式的推广：

两个三项式相乘，若他们的项中只存在         的项和                的项，则可以用平方差公式计算。它等于          的平方减去              的平方。

特别提示：把相反数的所有项看成一项。

即：

2. 完全平方公式的推广：

  一个三项式的平方，可以把前两项看成首项或后两项看成尾项，然后利用完全平方公式

的计算方法计算。

      即：

23．为了运用平方差公式计算（a﹣2b+c）（a+2b﹣c），下列变形中，正确的是（　　）

A．[（a+c）﹣2b][（a﹣c）+2b] B．[（a﹣2b）+c][（a+2b）﹣c] 

C．[a﹣（2b+c）][a+（2b﹣c）] D．[a﹣（2b﹣c）][a+（2b﹣c）]

24．为了便于直接应用平方差公式计算，应将（a+b﹣c）（a﹣b+c）变形为（　　）

A．[（a+b）﹣c][（a﹣b）+c] B．[a+（b﹣c）][a﹣（b﹣c）] 

C．[（a﹣c）+b][（a+c）﹣b] D．（a+b﹣c）[（a﹣b）+c]

一、选择题（10题）

1．下列多项式相乘，不能用平方差公式计算的是（　　）

A．（x+3y）（x﹣3y） B．（﹣2x+3y）（﹣2x﹣3y） 

C．（x﹣2y）（2y+x） D．（2x﹣3y）（3y﹣2x）

2．下列各式中，能用完全平方公式计算的是（　　）

A．（3a﹣2b）（﹣2b﹣3a） B．（3a+2b）（﹣3a﹣2b） 

C．（3a+2b）（﹣2a﹣3b） D．（3a﹣2b）（3a+2b）

3．下列计算正确的是（　　）

A．（x+y）2＝x2+y2 B．（x﹣y）2＝x2﹣2xy﹣y2 

C．（﹣x+y）2＝x2﹣2xy+y2 D．（x+2y）（x﹣2y）＝x2﹣2y2

4．若（3x+2y）2＝（3x﹣2y）2+A，则代数式A是（　　）

A．﹣12xy B．12xy C．24xy D．﹣24xy

5．已知x﹣y＝3，x y＝3，则（x+y）2的值为（　　）

A．24 B．18 C．21 D．12

6．如图（1），在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），把余下的部分拼成一个长方形，如图（2），此过程可以验证（　　）

A．（a+b）2＝a2+2ab+b2 B．（a﹣b）2＝a2﹣2ab+b2 

C．a2﹣b2＝（a+b）（a﹣b） D．（a+b）2＝（a﹣b）2+4ab

7．为了运用平方差公式计算（x+3y﹣z）（x﹣3y+z），下列变形正确的是（　　）

A．[x﹣（3y+z）]2 B．[（x﹣3y）+z][（x﹣3y）﹣z] 

C．[x﹣（3y﹣z）][x+（3y﹣z）] D．[（x+3y）﹣z][（x﹣3y）+z]

8．若|x+y﹣5|+（x y﹣3）2＝0，则x2+y2的值为（　　）

A．19 B．31 C．27 D．23

9．计算（a﹣b）（a+b）（a2+b2）（a4﹣b4）的结果是（　　）

A．a8+2a4b4+b8 B．a8﹣2a4b4+b8 

C．a8+b8 D．a8﹣b8

10．有两个正方形A，B，现将B放在A的内部如图甲，将A，B并排放置后构造新的正方形如图乙．若图甲和图乙中阴影部分的面积分别为和，则正方形A，B的面积之和为（　　）

A．3 B．3.5 C．4 D．4.5

二、填空题（6题）

11．计算：799×801﹣8002＝　     　．

12．计算：（a﹣b﹣c）2＝　                  　．

13．已知：x+＝3，则x2+＝　    　．

14．若x m﹣y n＝（x+y2）（x﹣y2）（x2+y4），则m＝　   　，n＝　   　．

15．已知（2021﹣a）2+（a﹣2019）2＝7，则代数式（2021﹣a）（a﹣2019）的值为 　    　．

16．计算：（5+1）（52+1）（54+1）（58+1）（516+1）+＝　     　．

三、解答题（4题）

17．已知（x+y）2＝1，（x﹣y）2＝49，求x2+y2与x y的值．

18．如图，AB＝a，P是线段AB上一点，分别以AP，PB为边作正方形．

（1）设AP＝x，求两个正方形的面积和S．

（2）当AP分别为和时，比较S的大小．

19．回答下列问题

（1）填空：x2+＝（x+）2﹣　   　＝（x﹣）2+　   　

（2）若a+＝5，则a2+＝　    　；

（3）若a2﹣3a+1＝0，求a2+的值．

20．【阅读材料】

我们知道，图形也是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数量关系，而运用代数思想也能巧妙地解决一些图形问题．

在一次数学活动课上，张老师准备了若干张如图1所示的甲、乙、丙三种纸片，其中甲种纸片是边长为x的正方形，乙种纸片是边长为y的正方形，丙种纸片是长为y，宽为x的长方形，并用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成了如图2所示的一个大正方形．

【理解应用】

（1）观察图2，用两种不同方式表示阴影部分的面积可得到一个等式，请你直接写出这个等式；

【拓展升华】

（2）利用（1）中的等式解决下列问题．

①已知a2+b2＝20，a+b＝6，求ab的值；

②已知（2021﹣c）（c﹣2019）＝1，求：

（2021﹣c）2+（c﹣2019）2的值．