山东省临朐县2022年中考数学仿真试卷含解析

这是一份山东省临朐县2022年中考数学仿真试卷含解析，共25页。试卷主要包含了下列方程中，两根之和为2的是，若点A，2cs 30°的值等于等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）
1．已知函数y=(k-1)x2-4x+4的图象与x轴只有一个交点,则k的取值范围是( )
A．k≤2且k≠1 B．k<2且k≠1
C．k=2 D．k=2或1
2．半径为3的圆中，一条弦长为4，则圆心到这条弦的距离是（　　）
A．3 B．4 C． D．
3．计算a•a2的结果是（　　）
A．a B．a2 C．2a2 D．a3
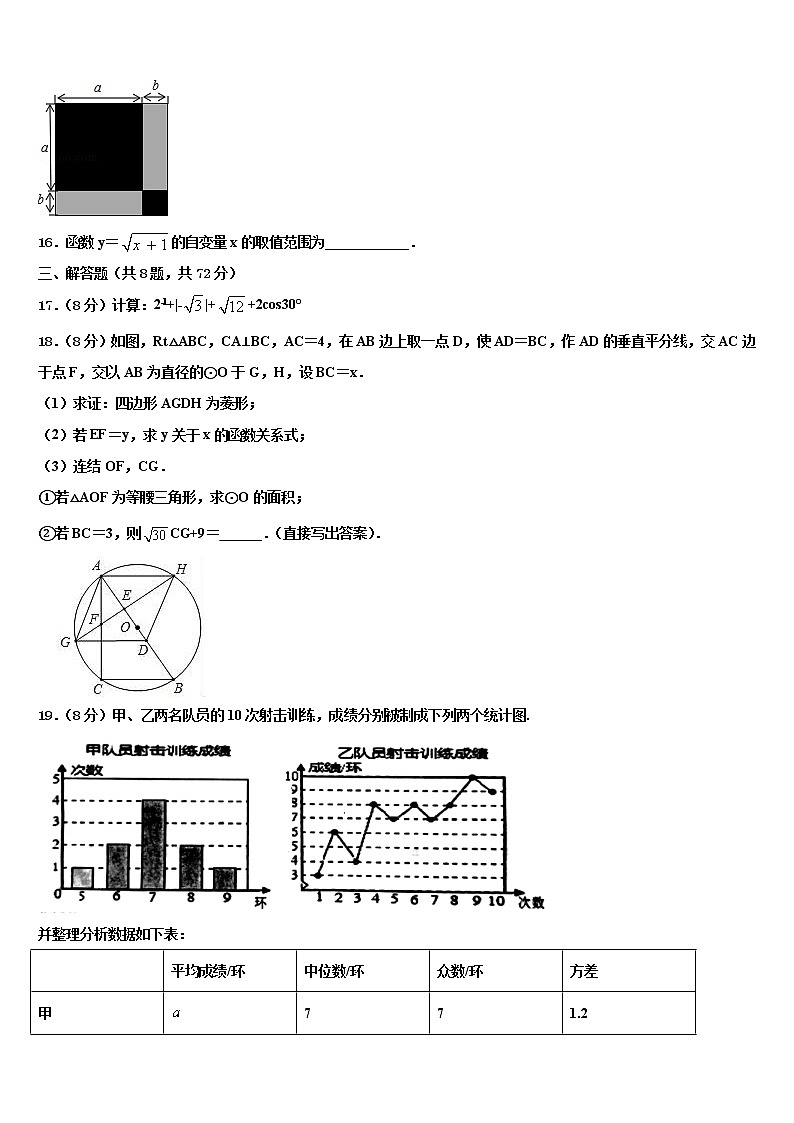
4．的绝对值是（　　）
A．﹣4 B． C．4 D．0.4
5．下列方程中，两根之和为2的是（　　）
A．x2+2x﹣3=0 B．x2﹣2x﹣3=0 C．x2﹣2x+3=0 D．4x2﹣2x﹣3=0
6．如图所示是由相同的小正方体搭成的几何体的俯视图，小正方形中的数字表示该位置上 小正方体的个数，那么该几何体的主视图是( )

A． B． C． D．
7．若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（　　）
A．﹣5 B．﹣3 C．3 D．1
8．2cos 30°的值等于(　　)
A．1 B． C． D．2
9．在下列四个新能源汽车车标的设计图中，属于中心对称图形的是（ ）
A． B． C． D．
10．若关于的一元二次方程有两个不相等的实数根，则一次函数
的图象可能是:
A． B． C． D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11．如图，在直角坐标系中，点A(2，0)，点B (0，1)，过点A的直线l垂直于线段AB，点P是直线l上一动点，过点P作PC⊥x轴，垂足为C，把△ACP沿AP翻折，使点C落在点D处，若以A，D，P为顶点的三角形与△ABP相似，则所有满足此条件的点P的坐标为___________________________．

12．在比例尺为1：50000的地图上，量得甲、乙两地的距离为12厘米，则甲、乙两地的实际距离是______千米．
13．如图，在3×3的正方形网格中，点A，B，C，D，E，F，G都是格点，从C，D，E，F，G五个点中任意取一点，以所取点及AB为顶点画三角形，所画三角形时等腰三角形的概率是_____.

14．甲、乙两个机器人检测零件，甲比乙每小时多检测20个，甲检测300个比乙检测200个所用的时间少，若设甲每小时检测个，则根据题意，可列出方程：__________．
15．如图，利用图形面积的不同表示方法，能够得到的代数恒等式是____________________(写出一个即可)．

16．函数y＝的自变量x的取值范围为____________．
三、解答题（共8题，共72分）
17．（8分）计算：2﹣1+|﹣|++2cos30°
18．（8分）如图，Rt△ABC，CA⊥BC，AC＝4，在AB边上取一点D，使AD＝BC，作AD的垂直平分线，交AC边于点F，交以AB为直径的⊙O于G，H，设BC＝x．
（1）求证：四边形AGDH为菱形；
（2）若EF＝y，求y关于x的函数关系式；
（3）连结OF，CG．
①若△AOF为等腰三角形，求⊙O的面积；
②若BC＝3，则CG+9＝______．（直接写出答案）．

19．（8分）甲、乙两名队员的10次射击训练，成绩分别被制成下列两个统计图.

并整理分析数据如下表：

平均成绩/环
中位数/环
众数/环
方差
甲

7
7
1.2
乙
7

8

（1）求，，的值；分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩.若选派其中一名参赛，你认为应选哪名队员？
20．（8分）某校要求八年级同学在课外活动中，必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练，为了了解八年级学生参加球类活动的整体情况，现以八年级(2)班作为样本，对该班学生参加球类活动的情况进行统计，并绘制了如图所示的不完整统计表和扇形统计图：
八年级(2)班参加球类活动人数情况统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
八年级(2)班学生参加球类活动人数情况扇形统计图

根据图中提供的信息，解答下列问题：a＝　 ，b＝　 ．该校八年级学生共有600人，则该年级参加足球活动的人数约　 人；该班参加乒乓球活动的5位同学中，有3位男同学(A，B，C)和2位女同学(D，E)，现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成混合双打组合的概率．
21．（8分）如图，在△ABC中，点D，E分别在边AB，AC上，∠AED=∠B，射线AG分别交线段DE，BC于点F，G，且．求证：△ADF∽△ACG；若，求的值．

22．（10分）在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．
（1）求抛物线解析式；
（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△MOA的面积为S．求S关于m的函数关系式，并求出当m为何值时，S有最大值，这个最大值是多少？
（3）若点Q是直线y=﹣x上的动点，过Q做y轴的平行线交抛物线于点P，判断有几个Q能使以点P，Q，B，O为顶点的四边形是平行四边形的点，直接写出相应的点Q的坐标．

23．（12分）（问题情境）
张老师给爱好学习的小军和小俊提出这样的一个问题：如图1，在△ABC中，AB＝AC，点P为边BC上任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F，求证：PD+PE＝CF．

小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE＝CF．
小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD＝GF，PE＝CG，则PD+PE＝CF．
[变式探究]
如图3，当点P在BC延长线上时，其余条件不变，求证：PD﹣PE＝CF；
请运用上述解答中所积累的经验和方法完成下列两题：
[结论运用]
如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD＝8，CF＝3，求PG+PH的值；
[迁移拓展]
图5是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D、C，且AD•CE＝DE•BC，AB＝2dm，AD＝3dm，BD＝dm．M、N分别为AE、BE的中点，连接DM、CN，求△DEM与△CEN的周长之和．
24．化简分式，并从0、1、2、3这四个数中取一个合适的数作为x的值代入求值.



参考答案

一、选择题（共10小题，每小题3分，共30分）
1、D
【解析】
当k+1=0时，函数为一次函数必与x轴有一个交点；当k+1≠0时，函数为二次函数，根据条件可知其判别式为0，可求得k的值．
【详解】
当k-1=0，即k=1时，函数为y=-4x+4，与x轴只有一个交点；
当k-1≠0，即k≠1时，由函数与x轴只有一个交点可知，
∴△=（-4）2-4（k-1）×4=0，
解得k=2，
综上可知k的值为1或2，
故选D．
【点睛】
本题主要考查函数与x轴的交点，掌握二次函数与x轴只有一个交点的条件是解题的关键，解决本题时注意考虑一次函数和二次函数两种情况．
2、C
【解析】
如图所示：
过点O作OD⊥AB于点D，

∵OB=3，AB=4，OD⊥AB，
∴BD=AB=×4=2，
在Rt△BOD中，OD=．
故选C．
3、D
【解析】
a·a2= a3.
故选D.
4、B
【解析】
分析：根据绝对值的性质，一个负数的绝对值等于其相反数，可有相反数的意义求解.
详解：因为-的相反数为
所以-的绝对值为.
故选：B
点睛：此题主要考查了求一个数的绝对值，关键是明确绝对值的性质，一个正数的绝对值等于本身，0的绝对值是0，一个负数的绝对值为其相反数.
5、B
【解析】
由根与系数的关系逐项判断各项方程的两根之和即可．
【详解】
在方程x2+2x-3=0中，两根之和等于-2，故A不符合题意；
在方程x2-2x-3=0中，两根之和等于2，故B符合题意；
在方程x2-2x+3=0中，△=（-2）2-4×3=-8＜0，则该方程无实数根，故C不符合题意；
在方程4x2-2x-3=0中，两根之和等于-，故D不符合题意，
故选B．
【点睛】
本题主要考查根与系数的关系，掌握一元二次方程的两根之和等于-、两根之积等于是解题的关键．
6、C
【解析】
A、B、D不是该几何体的视图，C是主视图，故选C.
【点睛】主视图是由前面看到的图形，俯视图是由上面看到的图形，左视图是由左面看到的图形，能看到的线画实线，看不到的线画虚线.
7、D
【解析】【分析】根据关于y轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变，据此求出m、n的值，代入计算可得．
【详解】∵点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，
∴1+m=3、1﹣n=2，
解得：m=2、n=﹣1，
所以m+n=2﹣1=1，
故选D．
【点睛】本题考查了关于y轴对称的点，熟练掌握关于y轴对称的两点的横坐标互为相反数，纵坐标不变是解题的关键.
8、C
【解析】
分析：根据30°角的三角函数值代入计算即可.
详解：2cos30°=2×=．
故选C．
点睛：此题主要考查了特殊角的三角函数值的应用，熟记30°、45°、60°角的三角函数值是解题关键.
9、D
【解析】
根据中心对称图形的概念求解．
【详解】
解：A．不是中心对称图形，本选项错误；
B．不是中心对称图形，本选项错误；
C．不是中心对称图形，本选项错误；
D．是中心对称图形，本选项正确．
故选D．
【点睛】
本题主要考查了中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180度后两部分重合．
10、B
【解析】
由方程有两个不相等的实数根,
可得，
解得，即异号，
当时，一次函数的图象过一三四象限，
当时，一次函数的图象过一二四象限，故答案选B.

二、填空题（本大题共6个小题，每小题3分，共18分）
11、
【解析】
∵点A(2，0)，点B (0，1)，
∴OA=2,OB=1, .
∵l⊥AB,
∴∠PAC＋OAB=90°.
∵∠OBA+∠OAB=90°,
∴∠OBA=∠PAC.
∵∠AOB=∠ACP,
∴△ABO∽△PAC,
.
设AC=m,PC=2m, .
当点P在x轴的上方时，
由 得, , ,
,PC=1,
,

由 得, , ∴m＝2,
∴AC=2,PC=4,
∴OC＝2+2=4,
∴P（4,4）.
当点P在x轴的下方时，

由 得, , ,
,PC=1,
,

由 得, , ∴m＝2,
∴AC=2,PC=4,
∴OC＝2-2=0,
∴P（0,4）.
所以P点坐标为或（4,4）或或（0,4）
【点睛】本题考察了相似三角形的判定，相似三角形的性质，平面直角坐标系点的坐标及分类讨论的思想.在利用相似三角形的性质列比例式时，要找好对应边，如果对应边不确定，要分类讨论.因点P在x轴上方和下方得到的结果也不一样，所以要分两种情况求解.
请在此填写本题解析!
12、
【解析】
本题可根据比例线段进行求解.
【详解】
解：因为在比例尺为1:50000的地图上甲，乙两地的距离12cm，所以，甲、乙的实际距离x满足12:x=1:50000，即x=12=600000cm=6km.
故答案为6.
【点睛】
本题主要考查比例尺和比例线段的相关知识.
13、.
【解析】
找出从C，D，E，F，G五个点中任意取一点组成等腰三角形的个数，再根据概率公式即可得出结论．
【详解】
∵从C，D，E，F，G五个点中任意取一点共有5种情况，其中A、B、C；A、B、F两种取法，可使这三定组成等腰三角形，
∴所画三角形时等腰三角形的概率是，
故答案是：．
【点睛】
考查的是概率公式，熟记随机事件A的概率P（A）＝事件A可能出现的结果数与所有可能出现的结果数的商是解答此题的关键．
14、
【解析】
【分析】若设甲每小时检测个，检测时间为，乙每小时检测个，检测时间为，根据甲检测300个比乙检测200个所用的时间少，列出方程即可.
【解答】若设甲每小时检测个，检测时间为，乙每小时检测个，检测时间为，根据题意有：
.
故答案为
【点评】考查分式方程的应用，解题的关键是找出题目中的等量关系.
15、（a+b）2=a2+2ab+b2
【解析】
完全平方公式的几何背景，即乘法公式的几何验证．此类题型可从整体和部分两个方面分析问题．本题从整体来看，整个图形为一个正方形，找到边长，表示出面积，从部分来看，该图形的面积可用两个小正方形的面积加上2个矩形的面积表示，从不同角度思考，但是同一图形，所以它们面积相等，列出等式.
【详解】
解：

,




【点睛】
此题考查了完全平方公式的几何意义，从不同角度思考，用不同的方法表示相应的面积是解题的关键.
16、x≥－1
【解析】
试题分析：由题意得，x+1≥0，解得x≥﹣1．故答案为x≥﹣1．
考点：函数自变量的取值范围．

三、解答题（共8题，共72分）
17、+4．
【解析】
原式利用负整数指数幂法则，二次根式性质，以及特殊角的三角函数值计算即可求出值．
【详解】
原式＝++2+2×＝+4．
【点睛】
本题考查了实数的运算，涉及了负整数指数幂、特殊角的三角函数值、二次根式的化简等，熟练掌握各运算的运算法则是解本题的关键．
18、（1）证明见解析；（2）y＝x2（x＞0）；（3）①π或8π或（2+2）π；②4．
【解析】
（1）根据线段的垂直平分线的性质以及垂径定理证明AG=DG=DH=AH即可；
（2）只要证明△AEF∽△ACB，可得解决问题；
（3）①分三种情形分别求解即可解决问题；
②只要证明△CFG∽△HFA，可得=，求出相应的线段即可解决问题；
【详解】
（1）证明：∵GH垂直平分线段AD，
∴HA＝HD，GA＝GD，
∵AB是直径，AB⊥GH，
∴EG＝EH，
∴DG＝DH，
∴AG＝DG＝DH＝AH，
∴四边形AGDH是菱形．
（2）解：∵AB是直径，
∴∠ACB＝90°，
∵AE⊥EF，
∴∠AEF＝∠ACB＝90°，
∵∠EAF＝∠CAB，
∴△AEF∽△ACB，
∴，
∴，
∴y＝x2（x＞0）．
（3）①解：如图1中，连接DF．

∵GH垂直平分线段AD，
∴FA＝FD，
∴当点D与O重合时，△AOF是等腰三角形，此时AB＝2BC，∠CAB＝30°，
∴AB＝，
∴⊙O的面积为π．
如图2中，当AF＝AO时，

∵AB＝＝，
∴OA＝，
∵AF＝＝，
∴＝，
解得x＝4（负根已经舍弃），
∴AB＝，
∴⊙O的面积为8π．
如图2﹣1中，当点C与点F重合时，设AE＝x，则BC＝AD＝2x，AB＝，

∵△ACE∽△ABC，
∴AC2＝AE•AB，
∴16＝x•，
解得x2＝2﹣2（负根已经舍弃），
∴AB2＝16+4x2＝8+8，
∴⊙O的面积＝π••AB2＝（2+2）π
综上所述，满足条件的⊙O的面积为π或8π或（2+2）π；
②如图3中，连接CG．

∵AC＝4，BC＝3，∠ACB＝90°，
∴AB＝5，
∴OH＝OA＝，
∴AE＝，
∴OE＝OA﹣AE＝1，
∴EG＝EH＝＝，
∵EF＝x2＝，
∴FG＝﹣，AF＝＝，AH＝＝，
∵∠CFG＝∠AFH，∠FCG＝∠AHF，
∴△CFG∽△HFA，
∴，
∴，
∴CG＝﹣，
∴CG+9＝4．
故答案为4．
【点睛】
本题考查圆综合题、相似三角形的判定和性质、垂径定理、线段的垂直平分线的性质、菱形的判定和性质、勾股定理、解直角三角形等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，学会用分类讨论的思想思考问题．
19、（1）a=7，b=7.5，c=4.2；（2）见解析.
【解析】
（1）利用平均数的计算公式直接计算平均分即可；将乙的成绩从小到大重新排列，用中位数的定义直接写出中位数即可；根据乙的平均数利用方差的公式计算即可；
（2）结合平均数和中位数、众数、方差三方面的特点进行分析．
【详解】
（1）甲的平均成绩a==7（环），
∵乙射击的成绩从小到大重新排列为：3、4、6、7、7、8、8、8、9、10，
∴乙射击成绩的中位数b==7.5（环），
其方差c=×[（3-7）2+（4-7）2+（6-7）2+2×（7-7）2+3×（8-7）2+（9-7）2+（10-7）2]
=×（16+9+1+3+4+9）
=4.2；
（2）从平均成绩看甲、乙二人的成绩相等均为7环，从中位数看甲射中7环以上的次数小于乙，从众数看甲射中7环的次数最多而乙射中8环的次数最多，从方差看甲的成绩比乙的成绩稳定；
综合以上各因素，若选派一名队员参加比赛的话，可选择乙参赛，因为乙获得高分的可能更大．
【点睛】
本题考查的是条形统计图和方差、平均数、中位数、众数的综合运用．熟练掌握平均数的计算，理解方差的概念，能够根据计算的数据进行综合分析．
20、 (1)a＝16，b＝17.5(2)90(3)
【解析】
试题分析：（1）首先求得总人数，然后根据百分比的定义求解；
（2）利用总数乘以对应的百分比即可求解；
（3）利用列举法，根据概率公式即可求解．
试题解析：（1）a=5÷12.5%×40%=16，5÷12.5%=7÷b%，∴b=17.5，故答案为16，17.5；
（2）600×[6÷（5÷12.5%）]=90（人），故答案为90；
（3）如图，∵共有20种等可能的结果，两名主持人恰为一男一女的有12种情况，∴则P（恰好选到一男一女）==．

考点：列表法与树状图法；用样本估计总体；扇形统计图．
21、 (1)证明见解析；（2）1.
【解析】
（1）欲证明△ADF∽△ACG，由可知，只要证明∠ADF=∠C即可．
（2）利用相似三角形的性质得到，由此即可证明．
【解答】（1）证明：∵∠AED=∠B，∠DAE=∠DAE，∴∠ADF=∠C，
∵，∴△ADF∽△ACG．
（2）解：∵△ADF∽△ACG，∴，
又∵，∴，
∴1．
22、（1）y=x2+x﹣4；（2）S关于m的函数关系式为S=﹣m2﹣2m+8，当m=﹣1时，S有最大值9；（3）Q坐标为（﹣4，4）或（﹣2+2，2﹣2）或（﹣2﹣2，2+2）时，使点P，Q，B，O为顶点的四边形是平行四边形．
【解析】
(1)设抛物线解析式为y＝ ax2 ＋ bx ＋ c,然后把点A、B、C的坐标代入函数解析式，利用待定系数法求解即可;
(2)利用抛物线的解析式表示出点M的纵坐标，从而得到点M到x轴的距离，然后根据三角形面积公式表示并整理即可得解，根据抛物线的性质求出第三象限内二次函数的最值，然后即可得解;
(3)利用直线与抛物线的解析式表示出点P、Q的坐标，然后求出PQ的长度，再根据平行四边形的对边相等列出算式，然后解关于x的一元二次方程即可得解.
【详解】
解：（1）设抛物线解析式为y=ax2+bx+c，
∵抛物线经过A（﹣4，0），B（0，﹣4），C（2，0），
∴，
解得，
∴抛物线解析式为y=x2+x﹣4；
（2）∵点M的横坐标为m，
∴点M的纵坐标为m2+m﹣4，
又∵A（﹣4，0），
∴AO=0﹣（﹣4）=4，
∴S=×4×|m2+m﹣4|=﹣（m2+2m﹣8）=﹣m2﹣2m+8，
∵S=﹣（m2+2m﹣8）=﹣（m+1）2+9，点M为第三象限内抛物线上一动点，
∴当m=﹣1时，S有最大值，最大值为S=9；
故答案为S关于m的函数关系式为S=﹣m2﹣2m+8，当m=﹣1时，S有最大值9；
（3）∵点Q是直线y=﹣x上的动点，
∴设点Q的坐标为（a，﹣a），
∵点P在抛物线上，且PQ∥y轴，
∴点P的坐标为（a，a2+a﹣4），
∴PQ=﹣a﹣（a2+a﹣4）=﹣a2﹣2a+4，
又∵OB=0﹣（﹣4）=4，
以点P，Q，B，O为顶点的四边形是平行四边形，
∴|PQ|=OB，
即|﹣a2﹣2a+4|=4，
①﹣a2﹣2a+4=4时，整理得，a2+4a=0，
解得a=0（舍去）或a=﹣4，
﹣a=4，
所以点Q坐标为（﹣4，4），
②﹣a2﹣2a+4=﹣4时，整理得，a2+4a﹣16=0，
解得a=﹣2±2，
所以点Q的坐标为（﹣2+2，2﹣2）或（﹣2﹣2，2+2），
综上所述，Q坐标为（﹣4，4）或（﹣2+2，2﹣2）或（﹣2﹣2，2+2）时，使点P，Q，B，O为顶点的四边形是平行四边形．
【点睛】
本题是对二次函数的综合考查有待定系数法求二次函数解析式，三角形的面积，二次函数的最值问题，平行四边形的对边相等的性质,平面直角坐标系中两点间的距离的表示，综合性较强，但难度不大，仔细分析便不难求解.
23、小军的证明：见解析；小俊的证明：见解析；[变式探究]见解析；[结论运用]PG+PH的值为1；[迁移拓展]（6+2）dm
【解析】
小军的证明：连接AP，利用面积法即可证得；
小俊的证明：过点P作PG⊥CF，先证明四边形PDFG为矩形，再证明△PGC≌△CEP，即可得到答案；
[变式探究]小军的证明思路：连接AP，根据S△ABC＝S△ABP﹣S△ACP，即可得到答案；
小俊的证明思路：过点C，作CG⊥DP，先证明四边形CFDG是矩形，再证明△CGP≌△CEP即可得到答案；
[结论运用] 过点E作EQ⊥BC，先根据矩形的性质求出BF，根据翻折及勾股定理求出DC，证得四边形EQCD是矩形，得出BE＝BF即可得到答案；
[迁移拓展]延长AD，BC交于点F，作BH⊥AF，证明△ADE∽△BCE得到FA=FB，设DH＝x，利用勾股定理求出x得到BH＝6，再根据∠ADE＝∠BCE＝90°，且M，N分别为AE，BE的中点即可得到答案.
【详解】
小军的证明：
连接AP，如图②

∵PD⊥AB，PE⊥AC，CF⊥AB，
∴S△ABC＝S△ABP+S△ACP，
∴AB×CF＝AB×PD+AC×PE，
∵AB＝AC，
∴CF＝PD+PE．
小俊的证明：
过点P作PG⊥CF，如图2，
∵PD⊥AB，CF⊥AB，PG⊥FC，
∴∠CFD＝∠FDG＝∠FGP＝90°，
∴四边形PDFG为矩形，
∴DP＝FG，∠DPG＝90°，
∴∠CGP＝90°，
∵PE⊥AC，
∴∠CEP＝90°，
∴∠PGC＝∠CEP，
∵∠BDP＝∠DPG＝90°，
∴PG∥AB，
∴∠GPC＝∠B，
∵AB＝AC，
∴∠B＝∠ACB，
∴∠GPC＝∠ECP，
在△PGC和△CEP中
，
∴△PGC≌△CEP，
∴CG＝PE，
∴CF＝CG+FG＝PE+PD；
[变式探究]
小军的证明思路：连接AP，如图③，

∵PD⊥AB，PE⊥AC，CF⊥AB，
∴S△ABC＝S△ABP﹣S△ACP，
∴AB×CF＝AB×PD﹣AC×PE，
∵AB＝AC，
∴CF＝PD﹣PE；
小俊的证明思路：
过点C，作CG⊥DP，如图③，
∵PD⊥AB，CF⊥AB，CG⊥DP，
∴∠CFD＝∠FDG＝∠DGC＝90°，
∴CF＝GD，∠DGC＝90°，四边形CFDG是矩形，
∵PE⊥AC，
∴∠CEP＝90°，
∴∠CGP＝∠CEP，
∵CG⊥DP，AB⊥DP，
∴∠CGP＝∠BDP＝90°，
∴CG∥AB，
∴∠GCP＝∠B，
∵AB＝AC，
∴∠B＝∠ACB，
∵∠ACB＝∠PCE，
∴∠GCP＝∠ECP，
在△CGP和△CEP中，
，
∴△CGP≌△CEP，
∴PG＝PE，
∴CF＝DG＝DP﹣PG＝DP﹣PE．
[结论运用]
如图④

过点E作EQ⊥BC，
∵四边形ABCD是矩形，
∴AD＝BC，∠C＝∠ADC＝90°，
∵AD＝8，CF＝3，
∴BF＝BC﹣CF＝AD﹣CF＝5，
由折叠得DF＝BF，∠BEF＝∠DEF，
∴DF＝5，
∵∠C＝90°，
∴DC＝＝1，
∵EQ⊥BC，∠C＝∠ADC＝90°，
∴∠EQC＝90°＝∠C＝∠ADC，
∴四边形EQCD是矩形，
∴EQ＝DC＝1，
∵AD∥BC，
∴∠DEF＝∠EFB，
∵∠BEF＝∠DEF，
∴∠BEF＝∠EFB，
∴BE＝BF，
由问题情景中的结论可得：PG+PH＝EQ，
∴PG+PH＝1．
∴PG+PH的值为1．
[迁移拓展]
延长AD，BC交于点F，作BH⊥AF，如图⑤，

∵AD×CE＝DE×BC，
∴，
∵ED⊥AD，EC⊥CB，
∴∠ADE＝∠BCE＝90°，
∴△ADE∽△BCE，
∴∠A＝∠CBE，
∴FA＝FB，
由问题情景中的结论可得：ED+EC＝BH，
设DH＝x，
∴AH＝AD+DH＝3+x，
∵BH⊥AF，
∴∠BHA＝90°，
∴BH2＝BD2﹣DH2＝AB2﹣AH2，
∵AB＝2，AD＝3，BD＝，
∴（）2﹣x2＝（2）2﹣（3+x）2，
∴x＝1，
∴BH2＝BD2﹣DH2＝37﹣1＝36，
∴BH＝6，
∴ED+EC＝6，
∵∠ADE＝∠BCE＝90°，且M，N分别为AE，BE的中点，
∴DM＝EM＝AE，CN＝EN＝BE，
∴△DEM与△CEN的周长之和
＝DE+DM+EM+CN+EN+EC
＝DE+AE+BE+EC
＝DE+AB+EC
＝DE+EC+AB
＝6+2，
∴△DEM与△CEN的周长之和（6+2）dm．
【点睛】
此题是一道综合题,考查三角形全等的判定及性质,勾股定理,矩形的性质定理,三角形的相似的判定及性质定理,翻折的性质,根据题中小军和小俊的思路进行证明,故正确理解题意由此进行后面的证明是解题的关键.
24、x取0时，为1 或x取1时，为2
【解析】
试题分析：利用分式的运算，先对分式化简单，再选择使分式有意义的数代入求值即可．
试题解析：解：原式=[]
=
=
= x＋1，
∵x1-4≠0，x-2≠0，
∴x≠1且x≠-1且x≠2，
当x=0时，原式=1．
或当x=1时，原式=2．