初中数学沪科版八年级上册第12章 一次函数12.2 一次函数集体备课课件ppt

这是一份初中数学沪科版八年级上册第12章 一次函数12.2 一次函数集体备课课件ppt，共29页。PPT课件主要包含了知识回顾，①当y0时，②当y0时，③当y0时，新课导入，探究1，从“函数值”的角度看，可转化为，x的值，得x-3等内容，欢迎下载使用。

点 P 在 x 轴上;
点 P 在 x 轴上方;
点 P 在 x 轴下方.
我们学习了平面直角坐标系 ，请同学们回顾一下：对点 P(x,y),当 y=0、y>0 、y<0 时，点 P 位于坐标平面内什么位置？
y>0
y<0
前面，已经学过一元一次方程和一元一次不等式的解法，
它们与一次函数之间有什么联系呢？
(1) 解方程：2x+6=0；
(2) 已知一次函数 y=2x+6，问 x 取何值时，y=0？
解：(1) 2x+6=0 2x=-6 x=-3
(2) 当 y=0 时 ，即 2x+6=0 2x=-6 x=-3
思考 ①：这两个问题有什么关系？
求一次函数 y=2x+6 中 y=0时
求一元一次方程 2x+6=0 的解，
思考②： 方程 2x+6=0 的解与一次函数 y=2x+6 的图象又有什么关系
(3) 画出函数 y=2x+6 的图象，并确定它与 x 轴的交点坐标.
从图中可以看出，一次函数 y=2x+6 的图象与x轴交点坐标为 ,
这就是当 y=0 时，
而 x=-3 正是方程 2x+6=0 的解.
从“函数图象”的角度看
与 x 轴交点的横坐标.
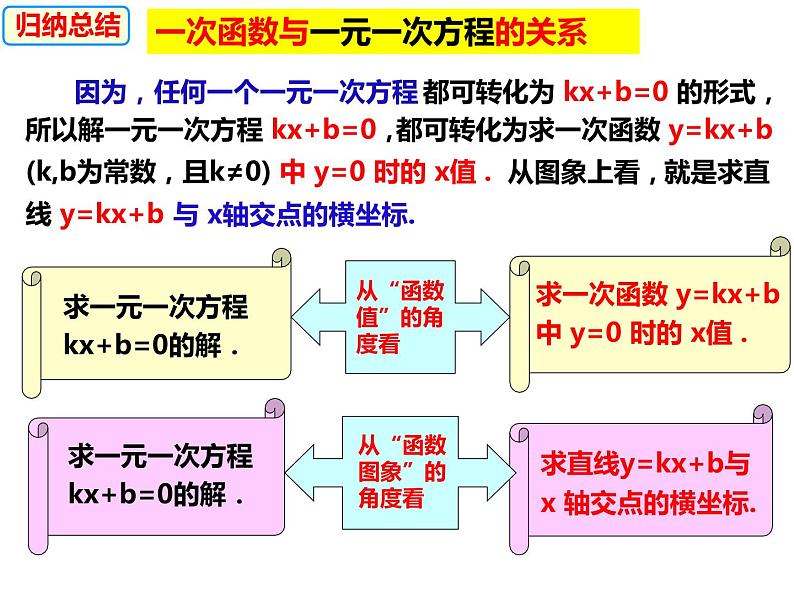
一次函数与一元一次方程的关系
因为，任何一个一元一次方程
都可转化为 kx+b=0 的形式，
所以解一元一次方程 kx+b=0，
都可转化为求一次函数 y=kx+b (k,b为常数，且k≠0) 中 y=0 时的 x值 .
就是求直线 y=kx+b
与 x轴交点的横坐标.
求一元一次方程kx+b=0的解．
求一次函数 y=kx+b 中 y=0 时的 x值 .
求直线y=kx+b与 x 轴交点的横坐标.
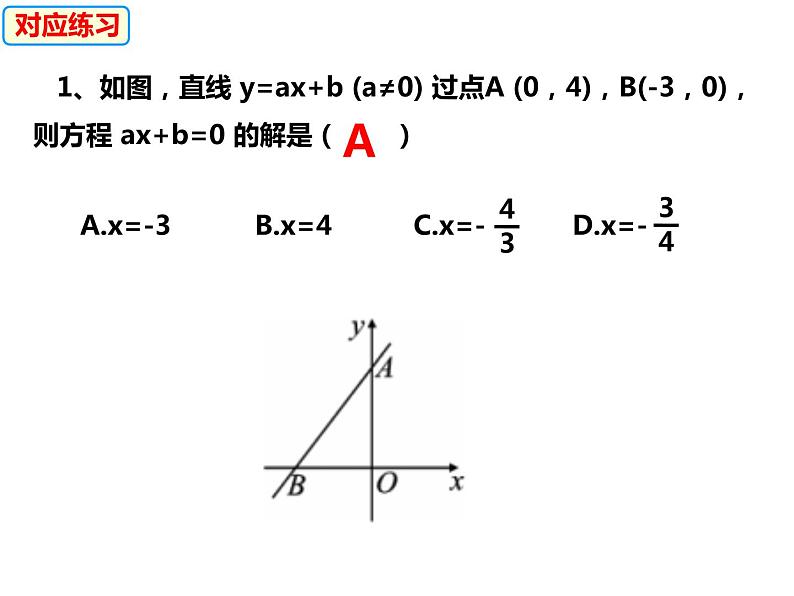
1、如图，直线 y=ax+b (a≠0) 过点A (0，4)，B(-3，0)，则方程 ax+b=0 的解是（　　）
A.x=-3 B.x=4 C.x=- D.x=-
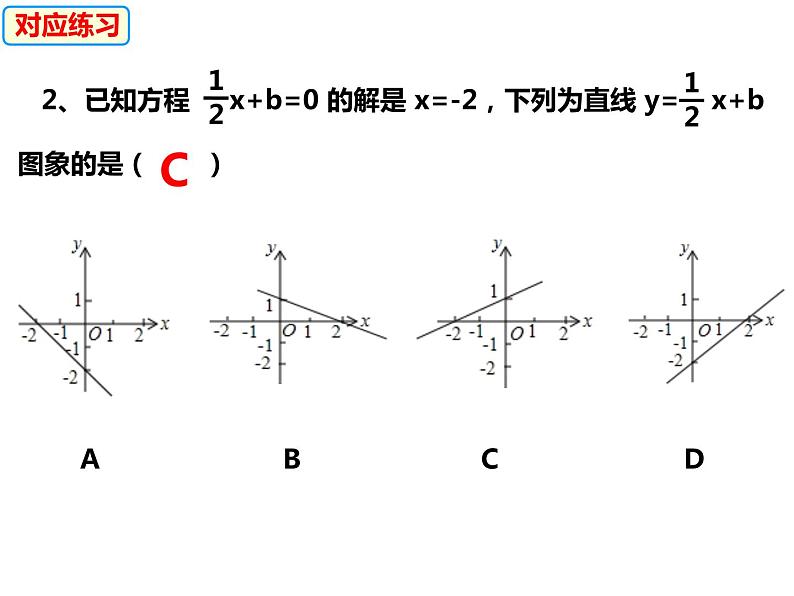
2、已知方程 x+b=0 的解是 x=-2，下列为直线 y= x+b图象的是（　　）
3、已知方程 2x+b=0 的解是 x=-5，则一次函数 y=2x+b 与 x 轴的交点坐标为 .
4、一次函数y=kx+b (k,b为常数,k≠0) 的图象如图所示，根据图象信息可求得关于x的方程 kx+b=3 的解为 .
　 5、下面三个方程有什么共同特点？你能从函数的角度对解这三个方程进行解释吗？ (1) 2x+1=3 (2) 2x+1=0 (3) 2x+1=-1．
用函数的观点看： 解一元一次方程 ax+b=k
对应的自变量 x 的值．
y=ax+b 中 y=k 时，
根据一次函数 y=2x+6 的图像，你能说出一元一次不等式 2x+6>0 的解集了？
就是函数y=2x+6中函数值 y>0；
y＞0 就是指 x 轴上方的图象；
因为图象与x轴交于点(-3,0),
所以由图象可知，
根据一次函数 y=2x+6 的图像，你能说出一元一次不等式 2x+6<0 的解集了？
就是函数y=2x+6中函数值 y<0；
y<0 就是指 x 轴下方的图象；
因为，任何一个一元一次不等式都可以转化为 kx+b>0 的形式，
解一元一次不等式 kx+b>0 (或 kx+b<0)，
一次函数与一元一次不等式的关系
就是求使一次函数 y=kx+b (k,b为常数，且k≠0)
取正值 (或负值) 时x的取值范围.
求kx+b＞0(或＜0)的解
就是求直线y= ax+b在x轴上方（或下方）的图象所对应的 x 取值范围
就是求一次函数y=kx+b中y>0(或y<0)时，x的范围
例 7 画出函数 y=-3x+6 的图象，结合图象： (1) 求方程 -3x+6=0 的解； (2) 求不等式 -3x+6＞0的解集和 -3x+6≤0 的解集；
解:(1) 画出函数y=-3x+6的 图象，
所以，方程 -3x+6=0 的解就是与 x 轴交点的横坐标：x=2
图象与x 轴交点坐标为 (2,0).
所以，不等式-3x+6＞0的解集是 x＜2；
(2) 由图象可知，y＞0 时 x 的取值范围是 x＜2
所以，不等式-3x+6≤0的解集是 x≤2；
由图象可知，y≤0 时 x 的取值范围是 x≤2
1、画出一次函数 y=-2x-6 的图象，结合图象求：
(1)x______时，y=0；
(2)x______时，y＞0；
(3)x______时，y＜0；
(4)x______时，y＞6.
2、画出函数 y=3x-9 的图像结合图象，结合图象：
(1)求方程3x-9=0的解；
(2)求不等式3x-9≤0的解集；
(3)当y=3时，求x的值；
(4)当y＞3时，求x的范围.
答：3x-9=0的解为x=3；
答：不等式3x-9≤0的解集为x≤3 ；
答： y=3时，x=4；
答：当y＞3时，x＞4.
3、已知一次函数 y=kx+b (k,b是常数,且k≠0)，x 与 y 的部分对应值如下表所示，那么不等式 kx+b＜0 的解集是（　　）
A.x＜0 B.x＞0 C.x＜2 D.x＞2
4、如图，已知函数 y1=3x+b 和 y2=ax-3 的图象交于点 P(-2,-5)，则不等式 3x+b＞ax-3 的解集为（　　）
A.x＞-2 B.x＜-2 C.x＞-5 D.x＜-5
就是直线 y1=k1x+b1 在直线y2=k2x+b2 上方部分对应 x 的取值范围.
5、如图，方程 k1x+b1=k2x+b2 的解为 ;
不等式 k1x+b1>k2x+b2 的解集为 ;
不等式 k1x+b1不等式 k1x+b1>k2x+b2 的解集
直线 y1=k1x+b1 与直线 y2=k2x+b2
方程 k1x+b1=k2x+b2
6、如图，直线 y1=-x+a 与 y2=bx-4 相交于点 P，已知点 P 的坐标为 (1，-3)，则关于 x 的不等式 -x+a＜bx-4 的解集是 .
7、如图，直线 y=kx+b (k,b是常数,k≠0) 与直线 y=2 交于点A (4,2)，则关于 x 的不等式 kx+b＜2 的解集为（　　）
A.x＜4 B.x≤4 C.x＞4 D.x＞2
8、如图，直线y=kx+b 经过点A (-1,-2) 和点B (-2,0)，直线 y=2x 过点A，则不等式 2x＜kx+b＜0 的解集为（　　）
A.x＜-2 B.-2＜x＜-1 C.-2＜x＜0 D.-1＜x＜0
9、如图，函数 y=2x 和 y=ax+4 的图象相交于点 A (m,3)，则不等式 2x＜ax+4 的解集为 .
9、如图，直线y=kx+b (k＜0) 经过点P (1，1)，当 kx+b≥x 时，则 x 的取值范围为（　　）
A.x≤1 B.x≥1C.x＜1 D.x＞1
10、若一次函数 y=kx+3 (k为常数且k≠0) 的图象经过点(-2，0)，则关于x的方程 k(x-5)+3=0的解为（　　）
A.x=-5 B.x=-3C.x=3D.x=5