河南省郑州市桐柏一中学2021-2022学年中考五模数学试题含解析

这是一份河南省郑州市桐柏一中学2021-2022学年中考五模数学试题含解析，共22页。试卷主要包含了考生要认真填写考场号和座位序号，不等式组的解集是，已知抛物线c等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．下面的统计图反映了我市2011﹣2016年气温变化情况，下列说法不合理的是（　　）

A．2011﹣2014年最高温度呈上升趋势
B．2014年出现了这6年的最高温度
C．2011﹣2015年的温差成下降趋势
D．2016年的温差最大
2．如图，已知BD与CE相交于点A，ED∥BC，AB=8，AC=12，AD=6，那么AE的长等于（ ）

A．4 B．9 C．12 D．16
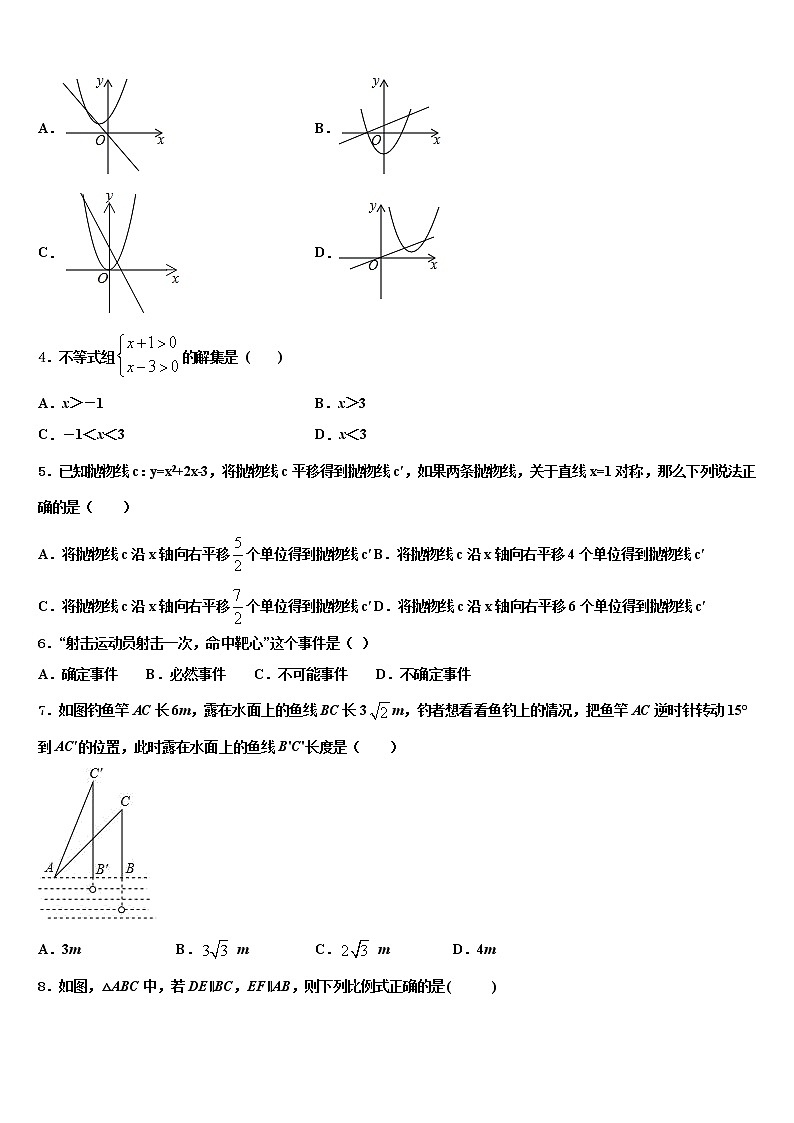
3．已知：如图是y＝ax2+2x﹣1的图象，那么ax2+2x﹣1＝0的根可能是下列哪幅图中抛物线与直线的交点横坐标（　　）

A． B．
C． D．
4．不等式组的解集是 (　　)
A．x＞－1 B．x＞3
C．－1＜x＜3 D．x＜3
5．已知抛物线c：y=x2+2x﹣3，将抛物线c平移得到抛物线c′，如果两条抛物线，关于直线x=1对称，那么下列说法正确的是（　　）
A．将抛物线c沿x轴向右平移个单位得到抛物线c′ B．将抛物线c沿x轴向右平移4个单位得到抛物线c′
C．将抛物线c沿x轴向右平移个单位得到抛物线c′ D．将抛物线c沿x轴向右平移6个单位得到抛物线c′
6．“射击运动员射击一次，命中靶心”这个事件是（ ）
A．确定事件 B．必然事件 C．不可能事件 D．不确定事件
7．如图钓鱼竿AC长6m，露在水面上的鱼线BC长3m，钓者想看看鱼钓上的情况，把鱼竿AC逆时针转动15°到AC′的位置，此时露在水面上的鱼线B'C'长度是（　　）

A．3m B． m C． m D．4m
8．如图，△ABC中，若DE∥BC，EF∥AB，则下列比例式正确的是( )

A． B．
C． D．
9．如图，点P是菱形ABCD边上的一动点，它从点A出发沿在A→B→C→D路径匀速运动到点D，设△PAD的面积为y，P点的运动时间为x，则y关于x的函数图象大致为（　　）

A． B． C． D．
10．将抛物线向右平移1个单位长度，再向上平移1个单位长度所得的抛物线解析式为（ ）
A． B．
C． D．
二、填空题（共7小题，每小题3分，满分21分）
11．如果，那么______．
12．2018年1月4日在萍乡市第十五届人民代表大会第三次会议报告指出，去年我市城镇居民人均可支配收入33080元，33080用科学记数法可表示为__．
13．如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y＝(k≠0，x＞0)的图象经过顶点C、D，若点C的横坐标为5，BE＝3DE，则k的值为______．

14．廊桥是我国古老的文化遗产如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，则这两盏灯的水平距离EF是______米精确到1米

15．甲、乙两人5次射击命中的环数分别为，甲：7，9，8，6，10；乙：7，8，9，8，8； =8，则这两人5次射击命中的环数的方差S甲2_____S乙2（填“＞”“＜”或“=”）．
16．如图，在平面直角坐标系xOy中，直线l：y=x-与x轴交于点B1，以OB1为边长作等边三角形A1OB1，过点A1作A1B2平行于x轴，交直线l于点B2，以A1B2为边长作等边三角形A2A1B2，过点A2作A2B3平行于x轴，交直线l于点B3，以A2B3为边长作等边三角形A3A2B3，…，按此规律进行下去，则点A3的横坐标为______；点A2018的横坐标为______．

17．分解因式：ax2－a=______．
三、解答题（共7小题，满分69分）
18．（10分）如图，在平面直角坐标系xOy中，已知正比例函数与一次函数的图像交于点A，
（1）求点A的坐标；
（2）设x轴上一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交和的图像于点B、C，连接OC，若BC=OA，求△OBC的面积.

19．（5分）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）画出△ABC关于点B成中心对称的图形△A1BC1；以原点O为位似中心，位似比为1：2，在y轴的左侧画出△ABC放大后的图形△A2B2C2，并直接写出C2的坐标．

20．（8分）如图，在△ABC中，AB=AC=1，BC=，在AC边上截取AD=BC，连接BD．
（1）通过计算，判断AD2与AC•CD的大小关系；
（2）求∠ABD的度数．

21．（10分）如图，已知△ABC内接于⊙O，BC交直径AD于点E，过点C作AD的垂线交AB的延长线于点G，垂足为F．连接OC．
（1）若∠G=48°，求∠ACB的度数；
（1）若AB=AE，求证：∠BAD=∠COF；
（3）在（1）的条件下，连接OB，设△AOB的面积为S1，△ACF的面积为S1．若tan∠CAF=，求的值．

22．（10分）当x取哪些整数值时，不等式与4﹣7x＜﹣3都成立？
23．（12分） (1)如图，四边形为正方形，，那么与相等吗？为什么？
(2)如图，在中，，，为边的中点，于点，交于，求的值
(3)如图，中，，为边的中点，于点，交于，若，，求.

24．（14分）如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0.1m）．（参考数据：≈1.414，≈1.732）




参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、C
【解析】
利用折线统计图结合相应数据，分别分析得出符合题意的答案．
【详解】
A选项：年最高温度呈上升趋势，正确；
B选项：2014年出现了这6年的最高温度，正确；
C选项：年的温差成下降趋势，错误；
D选项：2016年的温差最大，正确；
故选C．
【点睛】
考查了折线统计图，利用折线统计图获取正确信息是解题关键．
2、B
【解析】
由于ED∥BC，可证得△ABC∽△ADE，根据相似三角形所得比例线段，即可求得AE的长．
【详解】
∵ED∥BC，
∴△ABC∽△ADE，
∴ =，
∴ ==，
即AE=9；
∴AE=9.
故答案选B.
【点睛】
本题考查的知识点是相似三角形的判定与性质，解题的关键是熟练的掌握相似三角形的判定与性质.
3、C
【解析】
由原抛物线与x轴的交点位于y轴的两端，可排除A、D选项；
B、方程ax2+2x﹣1=0有两个不等实根，且负根的绝对值大于正根的绝对值，B不符合题意；
C、抛物线y=ax2与直线y=﹣2x+1的交点，即交点的横坐标为方程ax2+2x﹣1=0的根，C符合题意．此题得解．
【详解】
∵抛物线y=ax2+2x﹣1与x轴的交点位于y轴的两端，
∴A、D选项不符合题意；
B、∵方程ax2+2x﹣1=0有两个不等实根，且负根的绝对值大于正根的绝对值，
∴B选项不符合题意；
C、图中交点的横坐标为方程ax2+2x﹣1=0的根(抛物线y=ax2与直线y=﹣2x+1的交点)，
∴C选项符合题意．
故选：C．
【点睛】
本题考查了抛物线与x轴的交点以及二次函数的图象与位置变化，逐一分析四个选项中的图形是解题的关键．
4、B
【解析】
根据解不等式组的方法可以求得原不等式组的解集．
【详解】
，
解不等式①，得x＞-1，
解不等式②，得x＞1，
由①②可得，x＞1，
故原不等式组的解集是x＞1．
故选B．
【点睛】
本题考查解一元一次不等式组，解题的关键是明确解一元一次不等式组的方法．
5、B
【解析】
∵抛物线C：y=x2+2x﹣3=（x+1）2﹣4，
∴抛物线对称轴为x=﹣1．
∴抛物线与y轴的交点为A（0，﹣3）．
则与A点以对称轴对称的点是B（2，﹣3）．
若将抛物线C平移到C′，并且C，C′关于直线x=1对称，就是要将B点平移后以对称轴x=1与A点对称．
则B点平移后坐标应为（4，﹣3），
因此将抛物线C向右平移4个单位．
故选B．
6、D
【解析】
试题分析：“射击运动员射击一次，命中靶心”这个事件是随机事件，属于不确定事件，
故选D．
考点：随机事件．
7、B
【解析】
因为三角形ABC和三角形AB′C′均为直角三角形，且BC、B′C′都是我们所要求角的对边，所以根据正弦来解题，求出∠CAB，进而得出∠C′AB′的度数，然后可以求出鱼线B'C'长度．
【详解】
解：∵sin∠CAB＝
∴∠CAB＝45°．
∵∠C′AC＝15°，
∴∠C′AB′＝60°．
∴sin60°＝，
解得：B′C′＝3．
故选：B．
【点睛】
此题主要考查了解直角三角形的应用，解本题的关键是把实际问题转化为数学问题．
8、C
【解析】
根据平行线分线段成比例定理找准线段的对应关系，对各选项分析判断后利用排除法求解．
【详解】
解：∵DE∥BC，
∴＝，BD≠BC，
∴≠，选项A不正确；
∵DE∥BC，EF∥AB，
∴＝，EF=BD，＝，
∵≠，
∴≠，选项B不正确；
∵EF∥AB，
∴＝，选项C正确；
∵DE∥BC，EF∥AB，
∴＝，=，CE≠AE，
∴≠，选项D不正确；
故选C．
【点睛】
本题考查了平行线分线段成比例定理；熟练掌握平行线分线段成比例定理，在解答时寻找对应线段是关健．
9、B
【解析】【分析】设菱形的高为h，即是一个定值，再分点P在AB上，在BC上和在CD上三种情况，利用三角形的面积公式列式求出相应的函数关系式，然后选择答案即可．
【详解】分三种情况：
①当P在AB边上时，如图1，
设菱形的高为h，
y=AP•h，
∵AP随x的增大而增大，h不变，
∴y随x的增大而增大，
故选项C不正确；
②当P在边BC上时，如图2，
y=AD•h，
AD和h都不变，
∴在这个过程中，y不变，
故选项A不正确；
③当P在边CD上时，如图3，
y=PD•h，
∵PD随x的增大而减小，h不变，
∴y随x的增大而减小，
∵P点从点A出发沿A→B→C→D路径匀速运动到点D，
∴P在三条线段上运动的时间相同，
故选项D不正确，
故选B．

【点睛】本题考查了动点问题的函数图象，菱形的性质，根据点P的位置的不同，运用分类讨论思想，分三段求出△PAD的面积的表达式是解题的关键．
10、C
【解析】
试题分析：∵抛物线向右平移1个单位长度，∴平移后解析式为：，∴再向上平移1个单位长度所得的抛物线解析式为：．故选C．
考点：二次函数图象与几何变换．

二、填空题（共7小题，每小题3分，满分21分）
11、；
【解析】
先对等式进行转换，再求解.
【详解】
∵
∴3x＝5x－5y
∴2x＝5y
∴
【点睛】
本题考查的是分式，熟练掌握分式是解题的关键.
12、3.308×1．
【解析】
正确用科学计数法表示即可.
【详解】
解：33080=3.308×1
【点睛】
科学记数法的表示形式为的形式, 其中1<|a|<10,n为整数.确定n的值时, 要看把原数变成a时, 小数点移动了多少位, n的绝对值与小数点移动的位数相同. 当原数绝对值大于10时, n是正数; 当原数的绝对值小于1时,n是负数.
13、
【解析】
过点D作DF⊥BC于点F，由菱形的性质可得BC＝CD，AD∥BC，可证四边形DEBF是矩形，可得DF＝BE，DE＝BF，在Rt△DFC中，由勾股定理可求DE＝1，DF＝3，由反比例函数的性质可求k的值．
【详解】
如图，过点D作DF⊥BC于点F，

∵四边形ABCD是菱形，
∴BC＝CD，AD∥BC，
∵∠DEB＝90°，AD∥BC，
∴∠EBC＝90°，且∠DEB＝90°，DF⊥BC，
∴四边形DEBF是矩形，
∴DF＝BE，DE＝BF，
∵点C的横坐标为5，BE＝3DE，
∴BC＝CD＝5，DF＝3DE，CF＝5﹣DE，
∵CD2＝DF2+CF2，
∴25＝9DE2+(5﹣DE)2，
∴DE＝1，
∴DF＝BE＝3，
设点C(5，m)，点D(1，m+3)，
∵反比例函数y＝图象过点C，D，
∴5m＝1×(m+3)，
∴m＝，
∴点C(5，)，
∴k＝5×＝，
故答案为：
【点睛】
本题考查了反比例函数图象点的坐标特征，菱形的性质，勾股定理，求出DE的长度是本题的关键．
14、
【解析】
由于两盏E、F距离水面都是8m，因而两盏景观灯之间的水平距离就
是直线y=8与抛物线两交点的横坐标差的绝对值．
故有，
即，，．
所以两盏警示灯之间的水平距离为：
15、＞
【解析】
分别根据方差公式计算出甲、乙两人的方差，再比较大小．
【详解】
∵=8，∴=[（7﹣8）2+（9﹣8）2+（8﹣8）2+（6﹣8）2+（10﹣8）2]=（1+1+0+4+4）=2，=[（7﹣8）2+（8﹣8）2+（9﹣8）2+（8﹣8）2+（8﹣8）2]=（1+0+1+0+0）=0.4，∴＞．
故答案为：＞．
【点睛】
本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
16、
【解析】
利用一次函数图象上点的坐标特征可求出点B1的坐标，根据等边三角形的性质可求出点A1的坐标，同理可得出点B2、A2、A3的坐标，根据点An坐标的变化即可得出结论．
【详解】
当y=0时，有x-=0，
解得：x=1，
∴点B1的坐标为（1，0），
∵A1OB1为等边三角形，
∴点A1的坐标为（，）．
当y=时．有x-=，
解得：x=，
∴点B2的坐标为（，），
∵A2A1B2为等边三角形，
∴点A2的坐标为（，）．
同理，可求出点A3的坐标为（，），点A2018的坐标为（，）．
故答案为；．
【点睛】
本题考查了一次函数图象上点的坐标特征、等边三角形的性质以及规律型中点的坐标，根据一次函数图象上点的坐标特征结合等边三角形的性质找出点An横坐标的变化是解题的关键．
17、
【解析】
先提公因式，再套用平方差公式.
【详解】
ax2－a=a（x2-1）=
故答案为：
【点睛】
掌握因式分解的一般方法：提公因式法，公式法.

三、解答题（共7小题，满分69分）
18、（1）A(4，3)；（2）28.
【解析】
（1）点A是正比例函数与一次函数图像的交点坐标，把与联立组成方程组，方程组的解就是点A的横纵坐标；（2）过点A作x轴的垂线，在Rt△OAD中，由勾股定理求得OA的长，再由BC=OA求得OB的长，用点P的横坐标a表示出点B、C的坐标，利用BC的长求得a值，根据即可求得△OBC的面积.
【详解】
解：（1）由题意得: ，解得，
∴点A的坐标为（4,3）.
（2）过点A作x轴的垂线，垂足为D，

在Rt△OAD中，由勾股定理得，

∴.
∵P（a，0），∴B（a,）,C（a,-a+7），∴BC=，
∴，解得a=8.
∴.
19、（1）画图见解析；（2）画图见解析，C2的坐标为（﹣6，4）．
【解析】
试题分析：利用关于点对称的性质得出的坐标进而得出答案；
利用关于原点位似图形的性质得出对应点位置进而得出答案．
试题解析：(1)△A1BC1如图所示．

(2)△A2B2C2如图所示，点C2的坐标为(－6，4)．
20、（1）AD2=AC•CD．（2）36°．
【解析】
试题分析：（1）通过计算得到=，再计算AC·CD，比较即可得到结论；
（2）由，得到，即，从而得到△ABC∽△BDC，故有，从而得到BD=BC=AD，故∠A=∠ABD，∠ABC=∠C=∠BDC．
设∠A=∠ABD=x，则∠BDC=2x，∠ABC=∠C=∠BDC=2x，由三角形内角和等于180°，解得：x=36°，从而得到结论．
试题解析：（1）∵AD=BC=，∴==．
∵AC=1，∴CD==，∴；
（2）∵，∴，即，又∵∠C=∠C，∴△ABC∽△BDC，∴，又∵AB=AC，∴BD=BC=AD，∴∠A=∠ABD，∠ABC=∠C=∠BDC．
设∠A=∠ABD=x，则∠BDC=∠A+∠ABD=2x，∴∠ABC=∠C=∠BDC=2x，∴∠A+∠ABC+∠C=x+2x+2x=180°，解得：x=36°，∴∠ABD=36°．
考点：相似三角形的判定与性质．
21、（1）48°（1）证明见解析（3）
【解析】
（1）连接CD，根据圆周角定理和垂直的定义可得结论；
（1）先根据等腰三角形的性质得：∠ABE=∠AEB，再证明∠BCG=∠DAC，可得 ，则所对的圆周角相等，根据同弧所对的圆周角和圆心角的关系可得结论；
（3）过O作OG⊥AB于G，证明△COF≌△OAG，则OG=CF=x，AG=OF，设OF=a，则OA=OC=1x-a，根据勾股定理列方程得：（1x-a）1=x1+a1，则a=x，代入面积公式可得结论．
【详解】
（1）连接CD，
∵AD是⊙O的直径，
∴∠ACD=90°，
∴∠ACB+∠BCD=90°，
∵AD⊥CG，
∴∠AFG=∠G+∠BAD=90°，
∵∠BAD=∠BCD，
∴∠ACB=∠G=48°；
（1）∵AB=AE，
∴∠ABE=∠AEB，
∵∠ABC=∠G+∠BCG，∠AEB=∠ACB+∠DAC，
由（1）得：∠G=∠ACB，
∴∠BCG=∠DAC，
∴，
∵AD是⊙O的直径，AD⊥PC，
∴，
∴，
∴∠BAD=1∠DAC，
∵∠COF=1∠DAC，
∴∠BAD=∠COF；
（3）过O作OG⊥AB于G，设CF=x，
∵tan∠CAF== ，
∴AF=1x，
∵OC=OA，由（1）得：∠COF=∠OAG，
∵∠OFC=∠AGO=90°，
∴△COF≌△OAG，
∴OG=CF=x，AG=OF，
设OF=a，则OA=OC=1x﹣a，
Rt△COF中，CO1=CF1+OF1，
∴（1x﹣a）1=x1+a1，
a=x，
∴OF=AG=x，
∵OA=OB，OG⊥AB，
∴AB=1AG=x，
∴．

【点睛】
圆的综合题，考查了三角形的面积、垂径定理、角平分线的性质、三角形全等的性质和判定以及解直角三角形，解题的关键是：（1）根据圆周角定理找出∠ACB+∠BCD=90°；（1）根据外角的性质和圆的性质得：；（3）利用三角函数设未知数，根据勾股定理列方程解决问题．
22、2，1
【解析】
根据题意得出不等式组，解不等式组求得其解集即可．
【详解】
根据题意得，
解不等式①，得：x≤1，
解不等式②，得：x＞1，
则不等式组的解集为1＜x≤1，
∴x可取的整数值是2，1．
【点睛】
本题考查了解不等式组的能力，根据题意得出不等式组是解题的关键．
23、 (1)相等，理由见解析；(2)2；(3).
【解析】
（1）先判断出AB=AD，再利用同角的余角相等，判断出∠ABF=∠DAE，进而得出△ABF≌△DAE，即可得出结论；
（2）构造出正方形，同（1）的方法得出△ABD≌△CBG，进而得出CG=AB，再判断出△AFB∽△CFG，即可得出结论；
（3）先构造出矩形，同（1）的方法得，∠BAD=∠CBP，进而判断出△ABD∽△BCP，即可求出CP，再同（2）的方法判断出△CFP∽△AFB，建立方程即可得出结论．
【详解】
解：（1）BF=AE，理由：
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=∠D=90°，
∴∠BAE+∠DAE=90°，
∵AE⊥BF，
∴∠BAE+∠ABF=90°，
∴∠ABF=∠DAE，
在△ABF和△DAE中，
∴△ABF≌△DAE，
∴BF=AE，
(2) 如图2，
过点A作AM∥BC，过点C作CM∥AB，两线相交于M，延长BF交CM于G，

∴四边形ABCM是平行四边形，
∵∠ABC=90°，
∴▱ABCM是矩形，
∵AB=BC，
∴矩形ABCM是正方形，
∴AB=BC=CM，
同（1）的方法得，△ABD≌△BCG，
∴CG=BD，
∵点D是BC中点，
∴BD=BC=CM，
∴CG=CM=AB，
∵AB∥CM，
∴△AFB∽△CFG，
∴
(3) 如图3，

在Rt△ABC中，AB=3，BC=4，
∴AC=5，
∵点D是BC中点，
∴BD=BC=2，
过点A作AN∥BC，过点C作CN∥AB，两线相交于N，延长BF交CN于P，
∴四边形ABCN是平行四边形，
∵∠ABC=90°，∴▱ABCN是矩形，
同（1）的方法得，∠BAD=∠CBP，
∵∠ABD=∠BCP=90°，
∴△ABD∽△BCP，
∴
∴
∴CP=
同（2）的方法，△CFP∽△AFB，
∴
∴
∴CF=.
【点睛】
本题是四边形综合题，主要考查了正方形的性质和判定，平行四边形的判定，矩形的判定和性质，全等三角形的判定和性质，相似三角形的判定和性质，构造出（1）题的图形，是解本题的关键．
24、这棵树CD的高度为8.7米
【解析】
试题分析：首先利用三角形的外角的性质求得∠ACB的度数，得到BC的长度，然后在直角△BDC中，利用三角函数即可求解．
试题解析：∵∠CBD=∠A+∠ACB，
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°，
∴∠A=∠ACB，
∴BC=AB=10（米）．
在直角△BCD中，CD=BCsin∠CBD=10×=5≈5×1.732=8.7（米）．
答：这棵树CD的高度为8.7米．
考点：解直角三角形的应用