人教版八年级下册第十九章 一次函数综合与测试习题ppt课件

这是一份人教版八年级下册第十九章 一次函数综合与测试习题ppt课件，共41页。PPT课件主要包含了s＝10＋60t，75L，－3≤y≤4，1求乙的速度，附加题20分，y1＝2x－6等内容，欢迎下载使用。

一、选择题(每小题3分，共30分)　　　　　　　　　　　　　　　　　　　　　　　　
1.关于圆周长公式C＝2πR，下列说法正确的是(　　)A.π，R是变量；2为常量 B.C，R为变量；2，π为常量 C.R为变量；2，π，C为常量 D.C为变量；2，π，R为常量
2.函数y＝ 的自变量x的取值范围是(　　)
A.x≠－3 B.x≠3 C.x≤3 D.x≤－3
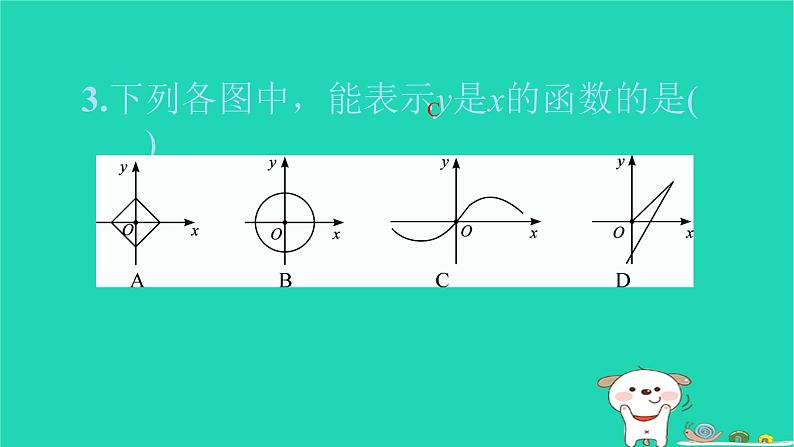
3.下列各图中，能表示y是x的函数的是(　　)
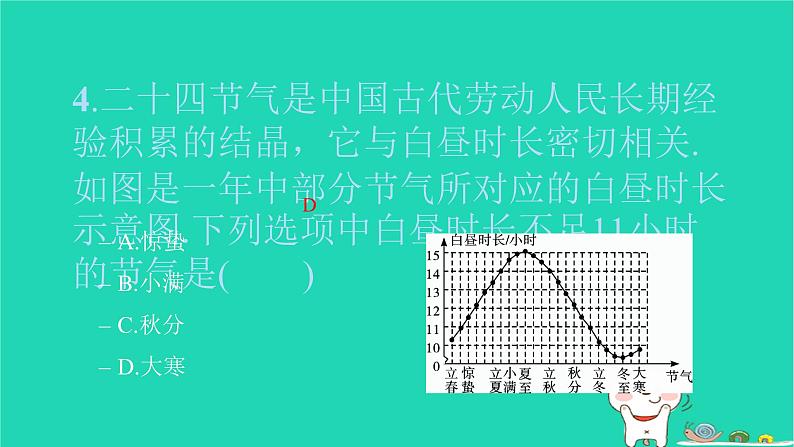
4.二十四节气是中国古代劳动人民长期经验积累的结晶，它与白昼时长密切相关.如图是一年中部分节气所对应的白昼时长示意图.下列选项中白昼时长不足11小时的节气是(　　)
A.惊蛰 B.小满 C.秋分 D.大寒
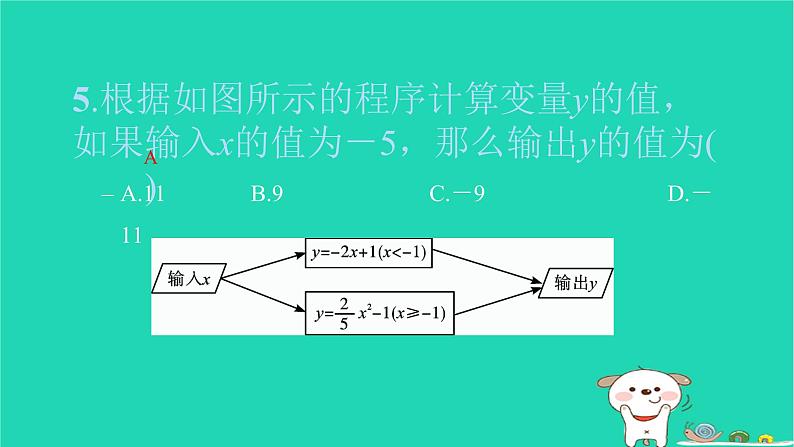
5.根据如图所示的程序计算变量y的值，如果输入x的值为－5，那么输出y的值为(　　)
A.11 B.9 C.－9 D.－11
6.某正方形的边长为4，如果边长增加x，那么面积增加y，则y关于x的函数解析式为(　　)
A.y＝x2＋16 B.y＝(x＋4)2 C.y＝x2＋8x D.y＝16－4x2
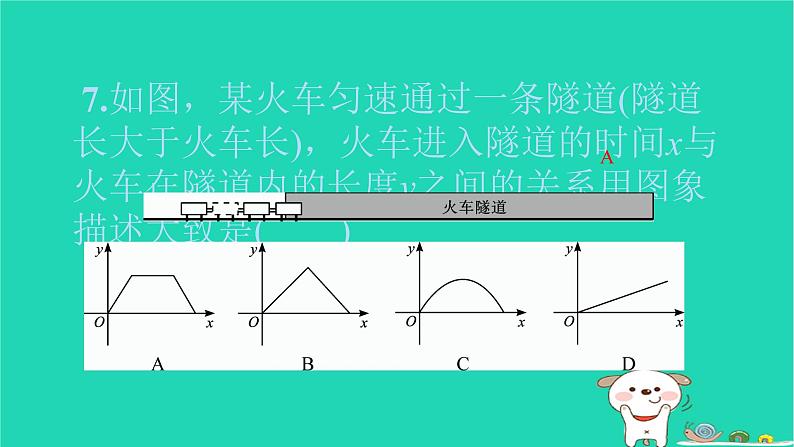
7.如图，某火车匀速通过一条隧道(隧道长大于火车长)，火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是(　　)
8.如图，用若干张长6 cm的纸片，重叠1 cm粘贴成一条纸带，纸带的长度y(cm)与纸片的张数x之间的函数解析式是(　　)
A.y＝6x－1 B.y＝6x＋1 C.y＝5x＋2 D.y＝5x＋1
9.已知弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表，则下列说法正确的是(　　)
A.y随x的增大而增大 B.质量每增加1 kg，长度增加0.5 cmC.不挂物体时，长度为6 cm D.质量为6 kg时，长度为8.5 cm
10.如图1，在菱形ABCD中，动点P从点B出发，沿折线B→C→D→B运动，设点P的路程为x，△ABP的面积为y.其中y关于x的函数图象如图2所示，则图中的a的值为(　　)
A.25 B.20 C.12 D.8
【解析】当x＝5时，BC＝5；当x＝10时，BC＋CD＝10，则CD＝5；当x＝18时，BC＋CD＋BD＝18，则BD＝8.过点C作CH⊥BD于点H，则BH＝DH＝4，∴CH＝ ＝3.当x＝5时，点P与点C重合，S△ABP＝S△ABC＝2S△BHC＝2× ×4×3＝12.故选C.
二、填空题(每小题3分，共24分)
11.骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一变量关系中，因变量是________.12.下列各式：①y＝x2；②y＝2x＋1；③y2＝2x(x≥0)；④y＝± (x≥0).其中具有函数关系(自变量为x)的是________.
13.汽车离开甲站10 km后，以60 km/h的速度匀速前进了t h，则汽车离开甲站所走的路程s(km)与时间t(h)之间的函数解析式是___________________.
14.小芳离开家不久，发现作业本落在家里，于是返回家找作业本，再去学校.如图所示的三个图象中，能近似地刻画上述情境的是________.(填序号)
15.某汽车生产厂对其生产的A型汽车进行油耗试验，试验中汽车为匀速行驶，在行使过程中，油箱的剩余油量y(L)与行驶时间t(h)之间的关系如下表：
由表格中y与t的关系可知，当汽车行驶________h，油箱的余油量为40 L.
16.观察如图所示的函数图象，当y随x的增大而增大时，x的取值范围是___________________，图象上纵坐标等于2.5的点有________个.
－4≤x≤－1或2≤x≤5
17.一个有进水管和出水管的容器，从某时刻开始4 min内只进水不出水，在随后的8 min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y(L)与时间x(min)之间的函数关系如图所示，则每分钟的出水量为________.
18.如图表示甲、乙两名选手在一次自行车越野赛中，行驶的路程y(千米)随时间x(分钟)变化的图象.下列结论：①比赛开始24分钟时，两人第一次相遇；②这次比赛全程是10千米；③比赛开始38分钟时，两人第二次相遇.正确的结论为________.(填序号)
三、解答题(共66分)
19.(8分)已知函数y＝ .(1)当x＝1或－1时，求y的值；
(2)当x为何值时，函数值y为1或－1?
20.(8分)已知函数y＝2x－6.
(1)画出该函数的图象；
(2)判断点A(4，3)是否在此函数的图象上；
(2)∵当x＝4时，y＝8－6＝2≠3，∴点A(4，3)不在此函数的图象上.
(3)当x＜3时，求y的取值范围.
(3)由图象可知，当x＜3时，y＜0.
21.(9分)已知某函数图象如图所示，根据图象解答下列问题：
(1)函数值y的取值范围是____________；(2)当x取何值时，y的值最小？并写出这个最小值；(3)当x＝0或x＝－5时，y的值分别是多少？
(2)当x＝－3时，y的值最小，y最小＝－3.
(3)当x＝0时，y＝2；当x＝－5时，y＝0.
22.(9分)某风景区集体门票的收费标准如下：20人以内(含20人)，每人25元；超过20人的，超过的部分每人10元.
(1)写出应收门票费y(元)与游览人数x(人)之间的函数解析式；
(2)某班54名学生去该风景区游览时，购买门票花了多少钱？
(2)当x＝54时，y＝10x＋300＝840(元)，∴购买门票花了840元.
23.(10分)甲、乙两人从A地出发，骑自行车沿同一条路行驶到B地，他们离出发地的距离s(单位：km)与行驶时间t(单位：h)之间的关系如图所示，且甲停留一段时间后再次行驶的速度是原来的一半，根据图象解答下列问题：
(2)甲中途停留了多长时间？
(3)求乙追上甲时，他们离B地的路程.
24.(10分)A，B两地相距360千米，甲车在A地，乙车在B地，两车同时出发，相向而行，在C地相遇，为节约费用(两车相遇并换货后，均需按原路返回出发地)，两车换货后，乙车因故障检修过程中甲车按原路返回A地，设两车在行驶过程中速度保持不变，两车间的距离y(千米)与时间x(小时)之间的函数关系如图所示，根据图中所提供的信息，解答下列问题：
(1)求甲、乙两车的速度；
解：(1)由题意知甲、乙两车的速度之和为 ＝180(千米/时)， ＝80(千米/时). ∵180＞80，∴换货后只有甲车运动， ∴甲车的速度为80千米/时，乙车的速度180－80＝100(千米/时).
(2)说明从两车开始出发到5小时这段时间内乙车的运动状态.
(2)乙车以100千米/时的速度从B地出发2个小时与甲车相遇，又在相遇点停留了3小时.
25.(12分)一游泳池长90米，甲、乙两人分别从两边同时向所对的另一边游去，到达另一边后，再返回，这样往复数次.如图所示的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况，请根据图象解答下列问题：
(1)甲、乙两人分别游了几个来回？
解：(1)甲游了3个来回，乙游了2个来回.
(2)甲、乙两人在整个游泳过程中，谁休息过？休息了几次？
(2)乙休息过，休息了两次.
(3)甲游了多长时间？速度是多少？
(3)甲游了180秒，游泳的速度是90×6÷180＝3(米/秒).
(4)在整个游泳过程中，甲、乙两人相遇了几次？
(4)甲、乙相遇了5次.
如图1，在长方形ABCD中，AB＝12 cm，BC＝10 cm，点P从点A出发，沿A→B→C→D的路线运动，到点D停止.点Q从点D出发，沿D→C→B→A路线运动，到点A停止.若P，Q两点同时出发，速度分别为每秒1 cm，2 cm，第a秒时P，Q两点同时改变速度，分别变为每秒2 cm， cm(P，Q两点速度改变后一直保持此速度运动，直到停止)，如图2是△APD的面积S(cm2)与运动时间x(s)之间的函数图象.(1)a的值为________；
(2)设点P已经运动的路程为y1(cm)，点Q还剩的路程为y2(cm)，则改变速度后，y1(cm)，y2(cm)与运动时间x(s)之间的函数解析式为______________，______________；
(3)P，Q两点都在边BC上，当x＝________时，P，Q两点相距3 cm.
【解析】(1)由图象可知，当点P在BC上运动时，△APD的面积保持不变，则第a s时，点P在AB上，S△APD＝ ×10AP＝30，∴AP＝6，即a的值为6. (2)由(1)可知，6 s后点P变速，则点P已经运动的路程为y1＝6＋2(x－6)＝2x－6.∵点Q路程总长为12＋10＋12＝34 (cm)，第6 s时，点Q已经运动了12 cm，∴点Q还剩的路程为y2＝34－12－ (x－6)＝－ x＋ .