

浙江省杭州市西湖区西溪中学2022-2023学年九年级上学期开学数学试卷(Word版含答案)
展开2022-2023学年浙江省杭州市西湖区西溪中学九年级(上)开学数学试卷(附答案与解析)
一、选择题(本题有10小题,每小题3分,共30分。请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.(3分)现有长度分别为2厘米、3厘米、4厘米、5厘米的木棒,从中任取三根,能组成三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
2.(3分)下列运算正确的是( )
A.﹣= B.3﹣=3 C.=﹣4 D.﹣=
3.(3分)二次函数y=(x﹣1)2+3图象的顶点坐标是( )
A.(1,3) B.(1,﹣3) C.(﹣1,3) D.(﹣1,﹣3)
4.(3分)令M=(a﹣x)(x﹣b),若,则( )
A.M<0 B.M>0 C.M≥0 D.M≤0
5.(3分)如图,直线l1:y=x+3与l2:y=mx+n交于点A(﹣1,b),则不等式x+3>mx+n的解集为( )
A.x≥﹣1 B.x<﹣1 C.x≤﹣1 D.x>﹣1
6.(3分)已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是( )
A.30° B.60° C.150° D.30°或150°
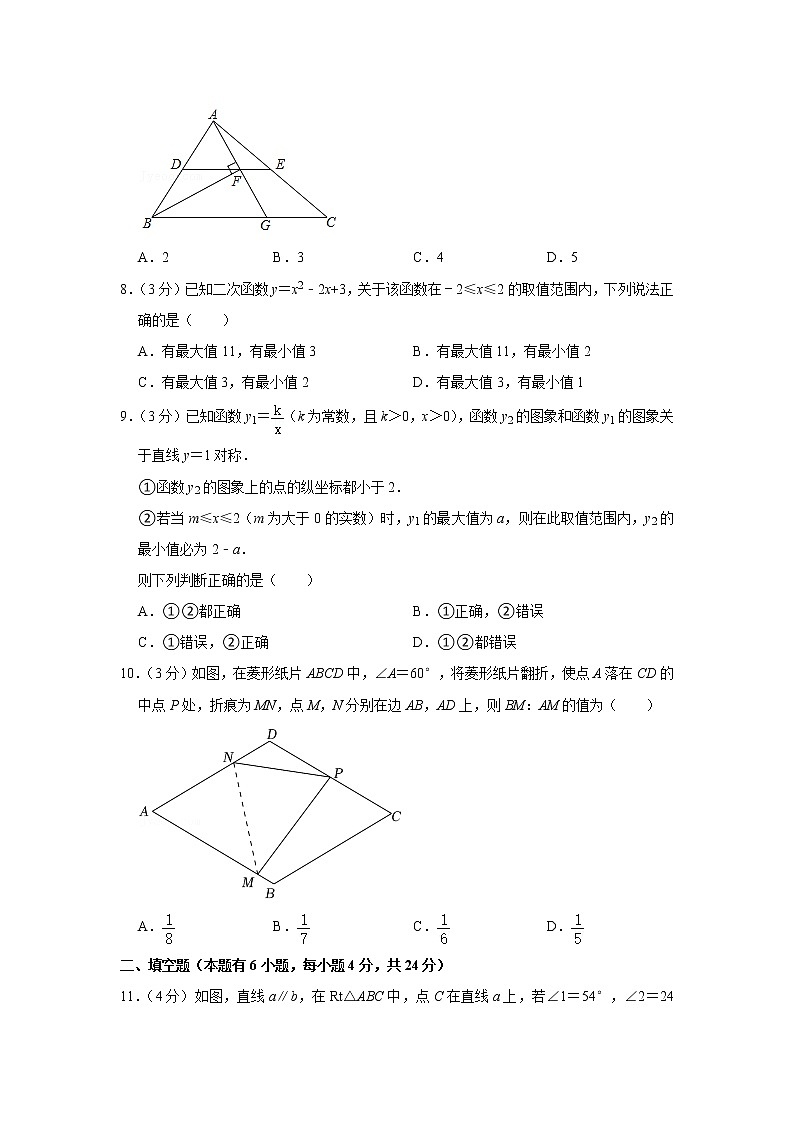
7.(3分)如图,在△ABC中,BF平分∠ABC,过A点作AF⊥BF,垂足为F并延长交BC于点G,D为AB中点,连接DF延长交AC于点E.若AB=12,BC=20,则线段EF的长为( )
A.2 B.3 C.4 D.5
8.(3分)已知二次函数y=x2﹣2x+3,关于该函数在﹣2≤x≤2的取值范围内,下列说法正确的是( )
A.有最大值11,有最小值3 B.有最大值11,有最小值2
C.有最大值3,有最小值2 D.有最大值3,有最小值1
9.(3分)已知函数y1=(k为常数,且k>0,x>0),函数y2的图象和函数y1的图象关于直线y=1对称.
①函数y2的图象上的点的纵坐标都小于2.
②若当m≤x≤2(m为大于0的实数)时,y1的最大值为a,则在此取值范围内,y2的最小值必为2﹣a.
则下列判断正确的是( )
A.①②都正确 B.①正确,②错误
C.①错误,②正确 D.①②都错误
10.(3分)如图,在菱形纸片ABCD中,∠A=60°,将菱形纸片翻折,使点A落在CD的中点P处,折痕为MN,点M,N分别在边AB,AD上,则BM:AM的值为( )
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.(4分)如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=54°,∠2=24°,则∠B的度数为 .
12.(4分)已知a=﹣2,则+a= .
13.(4分)已知4个正数a1,a2,a3,a4的平均数是a,且a1>a2>a3>a4,则数据a1,a2,0,a3,a4的平均数和中位数分别是 , .
14.(4分)一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(Ω),通过的电流强度为I(A),由欧姆定律可知,I=.当电阻为40Ω时,测得通过的电流强度为0.3A.为保证电流强度不低于0.2A且不超过0.6A,则选用灯泡电阻R的取值范围是 .
15.(4分)如图两张长相等,宽分别是1和3的矩形纸片上叠合在一起,重叠部分为四边形ABCD,且AB+BC=6,则四边形ABCD的面积为 .
16.(4分)如图是一张矩形纸片ABCD,点E在AC边上,把△DCE沿直线DE折叠,使点C落在对角线BD上的点F处;点G在AB边上,把△DAG沿直线DG折叠,使点A落在线段DF上的点H处.若HF=1,BF=8,则BD= ,矩形ABCD的面积= .
三、解答题(本题有7小题,共66分)
17.(6分)△ABC的周长为12,AC=2AB,设AB=x,BC=y.
(1)求y关于x的函数表达式,并写出自变量x的取值范围;
(2)若△ABC是等腰三角形,求它的三边长.
18.(8分)关于x,y的方程组,若2<x﹣y<4,则k的取值范围是多少?
19.(8分)已知一元二次方程(k﹣2)x2﹣4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
20.(10分)设一次函数y1=kx﹣2k(k是常数,且k≠0).
(1)若函数y1的图象经过点(﹣1,5),求函数y1的表达式.
(2)已知点P(x1,m)和Q(﹣3,n)在函数y1的图象上,若m>n,求x1的取值范围.
(3)若一次函数y2=ax+b(a≠0)的图象与y1的图象始终经过同一定点,探究实数a,b满足的关系式.
21.(10分)如图,ABCD是矩形纸片,翻折∠B,∠D,使BC,AD恰好落在AC上.设F,H分别是B,D落在AC上的两点,E,G分别是折痕CE,AG与AB,CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
22.(12分)在直角坐标系中,设反比例函数与一次函数y2=k2x+b(k2≠0)的图象都经过点A和点B,点A的坐标为(1,m),点B的坐标为(﹣2,﹣2).
(1)求m的值和一次函数y2的表达式.
(2)当y1>y2时,直接写出x的取值范围.
(3)把函数y2的图象向下平移n(n>0)个单位后,与函数y1的图象交于点(p1,q1)和(p2,q2),当p1=﹣1时,求此时n及p2×q2的值.
23.(12分)在正方形ABCD中,对角线AC与BD相交于点O,点E是线段OC上的动点.
(1)如图1,若DE平分∠CDO.
①求证:AD=AE.
②若CE=2,求OE的长.
(2)如图2,延长DE交BC于点F连接OF.当DF=2OF时,探究CF与AD的数量关系,并说明理由.
2022-2023学年浙江省杭州市西湖区西溪中学九年级(上)开学数学试卷
参考答案与试题解析
一、选择题(本题有10小题,每小题3分,共30分。请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.(3分)现有长度分别为2厘米、3厘米、4厘米、5厘米的木棒,从中任取三根,能组成三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】首先每3个搭配出所有情况,再根据三角形的三边关系进行排除.
【解答】解:首先任取三根,有2,3,4;2,3,5;2,4,5;3,4,5
再根据三角形的三边关系,得其中2+3=5,排除2,3,5,
只有3个符合.
故选:C.
【点评】考查了三角形的三边关系:两边之和大于第三边,两边之差小于第三边.
2.(3分)下列运算正确的是( )
A.﹣= B.3﹣=3 C.=﹣4 D.﹣=
【分析】直接利用二次根式的加减运算法则计算得出答案.
【解答】解:A、﹣=2﹣,故此选项错误;
B、3﹣=2,故此选项错误;
C、=4,故此选项错误;
D、﹣=2﹣=,正确.
故选:D.
【点评】此题主要考查了二次根式的加减运算,正确掌握运算法则是解题关键.
3.(3分)二次函数y=(x﹣1)2+3图象的顶点坐标是( )
A.(1,3) B.(1,﹣3) C.(﹣1,3) D.(﹣1,﹣3)
【分析】由抛物线顶点式可求得答案.
【解答】解:∵y=(x﹣1)2+3,
∴顶点坐标为(1,3),
故选:A.
【点评】本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x﹣h)2+k中,对称轴为x=h,顶点坐标为(h,k).
4.(3分)令M=(a﹣x)(x﹣b),若,则( )
A.M<0 B.M>0 C.M≥0 D.M≤0
【分析】根据x的取值范围来确定(a﹣x)与(x﹣b)的符号,从而得到M的取值范围.
【解答】解:∵,
∴a﹣x>0,x﹣b≤0.
∴(a﹣x)(x﹣b)≤0,即M≤0.
故选:D.
【点评】考查了一元一次不等式的应用,解题过程中,需要熟悉不等式的性质,难度不大.
5.(3分)如图,直线l1:y=x+3与l2:y=mx+n交于点A(﹣1,b),则不等式x+3>mx+n的解集为( )
A.x≥﹣1 B.x<﹣1 C.x≤﹣1 D.x>﹣1
【分析】观察函数图象得到,当x>﹣1时,直线L1:y=x+3的图象都在L2:y=mx+n的图象的上方,由此得到不等式x+3>mx+n的解集.
【解答】解:∵直线L1:y=x+3与L2:y=mx+n交于点A(﹣1,b),
从图象可以看出,当x>﹣1时,直线L1:y=x+3的图象都在L2:y=mx+n的图象的上方,
∴不等式x+3>mx+n的解集为:x>﹣1,
故选:D.
【点评】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
6.(3分)已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是( )
A.30° B.60° C.150° D.30°或150°
【分析】读到此题我们首先想到等腰三角形分为锐角、直角、钝角等腰三角形,当为等腰直角三角形时不可能出现题中所说情况所以舍去不计,我们可以通过画图来讨论剩余两种情况.
【解答】解:①当为锐角三角形时可以画图,
高与左边腰成60°夹角,由三角形内角和为180°可得,顶角为30°,
②当为钝角三角形时可画图,
此时垂足落到三角形外面,因为三角形内角和为180°,
由图可以看出等腰三角形的顶角的补角为30°,
∴三角形的顶角为150°,
故选:D.
【点评】本题主要考查了等腰三角形的性质及三角形内角和定理,做题时,考虑问题要全面,必要的时候可以做出模型帮助解答,进行分类讨论是正确解答本题的关键,难度适中.
7.(3分)如图,在△ABC中,BF平分∠ABC,过A点作AF⊥BF,垂足为F并延长交BC于点G,D为AB中点,连接DF延长交AC于点E.若AB=12,BC=20,则线段EF的长为( )
A.2 B.3 C.4 D.5
【分析】证明△BFA≌△BFG,根据全等三角形的性质得到BG=AB=12,AF=FG,根据三角形中位线定理计算即可.
【解答】解:在△BFA和△BFG中,
,
∴△BFA≌△BFG(ASA)
∴BG=AB=12,AF=FG,
∴GC=BC﹣BG=8,
∵AD=DB,AF=FG,
∴DE∥BC,
∵AE=EC,
∴AE=EC,AF=FG,
∴EF=GC=4,
故选:C.
【点评】本题考查的是三角形中位线定理、全等三角形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
8.(3分)已知二次函数y=x2﹣2x+3,关于该函数在﹣2≤x≤2的取值范围内,下列说法正确的是( )
A.有最大值11,有最小值3 B.有最大值11,有最小值2
C.有最大值3,有最小值2 D.有最大值3,有最小值1
【分析】根据题目中的函数解析式和二次函数的性质,可以得到该函数的对称轴和开口方向,然后根据﹣2≤x≤2,即可得到相应的最大值和最小值,从而可以解答本题.
【解答】解:∵二次函数y=x2﹣2x+3=(x﹣1)2+2,
∴该函数的对称轴是直线x=1,函数图象开口向上,
∴在﹣2≤x≤2的取值范围内,当x=﹣2时取得最大值11,当x=1时,取得最小值2,
故选:B.
【点评】本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确二次函数的性质,求出相应的最值.
9.(3分)已知函数y1=(k为常数,且k>0,x>0),函数y2的图象和函数y1的图象关于直线y=1对称.
①函数y2的图象上的点的纵坐标都小于2.
②若当m≤x≤2(m为大于0的实数)时,y1的最大值为a,则在此取值范围内,y2的最小值必为2﹣a.
则下列判断正确的是( )
A.①②都正确 B.①正确,②错误
C.①错误,②正确 D.①②都错误
【分析】根据反比例函数的性质以及轴对称的性质判断即可.
【解答】解:∵函数y1=(k为常数,且k>0,x>0),
∴函数y1=图象在第一象限,如图,
∴函数y的最小值大于0,
∵函数y2的图象和函数y1的图象关于直线y=1对称,
∴y2的最大值小于2,
∴函数y2的图象上的点的纵坐标都小于2.故①正确;
当m≤x≤2(m为大于0的实数)时,y1的最大值为a,则其对应点为(m,a),
那么,点(m,a)关于直线y=1的对称点为(m,2﹣a),
∴在此取值范围内,y2的最小值必为2﹣a,故②正确,
故选:A.
【点评】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,坐标与图形变化﹣对称,数形结合是解题的关键.
10.(3分)如图,在菱形纸片ABCD中,∠A=60°,将菱形纸片翻折,使点A落在CD的中点P处,折痕为MN,点M,N分别在边AB,AD上,则BM:AM的值为( )
A. B. C. D.
【分析】由菱形的性质和等边三角形的性质,可得BP⊥CD,DP=a,∠DBP=30°,由勾股定理可求解.
【解答】解:如图,连接BD,BP,
设AB=2a,
∵四边形ABCD是菱形,∠A=60°,
∴AB=BC=2a=CD,∠A=∠C=60°,
∴△BCD是等边三角形,△ABD是等边三角形,
∵点P在CD的中点,
∴BP⊥CD,DP=a,∠DBP=30°,
∴BP=a,∠ABP=∠ABD+∠DBP=90°,
∵将菱形纸片翻折,
∴AM=MP,
∵MP2=MB2+BP2,
∴(2a﹣BM)2=MB2+3a2,
∴BM=a,
∴AM=a,
∴BM:AM=,
故选:B.
【点评】本题考查了翻折变换,等边三角形的性质,菱形的性质,勾股定理,添加恰当的辅助线构造直角三角形是本题的关键.
二、填空题(本题有6小题,每小题4分,共24分)
11.(4分)如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=54°,∠2=24°,则∠B的度数为 60° .
【分析】利用平行线的性质,三角形的外角的性质求出∠A即可解决问题.
【解答】解:如图,
∵a∥b,
∴∠1=∠3=54°,
∵∠3=∠2+∠A,
∴∠A=54°﹣24°=30°,
∵∠ACB=90°,
∴∠B=90°﹣30°=60°,
故答案为60°.
【点评】本题考查平行线的性质,三角形的外角的性质,三角形的内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
12.(4分)已知a=﹣2,则+a= 0 .
【分析】根据二次根式的性质即可求出答案.
【解答】解:当a=﹣2时,
原式=|a|+a
=﹣a+a
=0;
故答案为:0
【点评】本题考查二次根式,解题的关键是熟练运用二次根式的性质,本题属于基础题型.
13.(4分)已知4个正数a1,a2,a3,a4的平均数是a,且a1>a2>a3>a4,则数据a1,a2,0,a3,a4的平均数和中位数分别是 a , a3 .
【分析】直接利用算术平均数求法,总数÷数据个数=平均数,再利用中位数的定义,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,即可得出答案.
【解答】解:由算术平均数定义可知:(a1+a2+0+a3+a4)=×4a=a;
将这组数据按从小到大排列为0,a4,a3,a2,a1;
由于有奇数个数,取最中间的数,
∴其中位数为a3.
故答案为:a,a3.
【点评】此题主要考查了中位数和算术平均数,正确掌握定义是解题关键.
14.(4分)一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(Ω),通过的电流强度为I(A),由欧姆定律可知,I=.当电阻为40Ω时,测得通过的电流强度为0.3A.为保证电流强度不低于0.2A且不超过0.6A,则选用灯泡电阻R的取值范围是 20≤R≤60 .
【分析】利用待定系数法可得I=,然后根据题意可得0.2≤I≤0.6,从而可得0.2≤≤0.6,然后进行计算即可解答.
【解答】解:由题意得:
I=,
∵当电阻为40Ω时,测得通过的电流强度为0.3A,
∴U=IR=0.3×40=12(V),
∴I=,
当0.2≤I≤0.6时,
∴0.2≤≤0.6,
∴20≤R≤60,
故答案为:20≤R≤60.
【点评】本题考查了反比例函数的应用,熟练掌握待定系数法求反比例函数解析式是解题的关键.
15.(4分)如图两张长相等,宽分别是1和3的矩形纸片上叠合在一起,重叠部分为四边形ABCD,且AB+BC=6,则四边形ABCD的面积为 4.5 .
【分析】根据题意判定四边形ABCD是平行四边形.如图,过点A作AE⊥BC于点E,过点A作AF⊥CD于点F,利用面积法求得AB与BC的数量关系,从而求得该平行四边形的面积.
【解答】解:依题意得:AB∥CD,AD∥BC,则四边形ABCD是平行四边形.
如图,过点A作AE⊥BC于点E,过点A作AF⊥CD于点F,
∴AE=1,AF=3,
∴BC•AE=AB•AF,
∴BC=3AB.
又∵AB+BC=6,
∴AB=1.5,BC=4.5,
∴四边形ABCD的面积=4.5×1=4.5.
故答案为:4.5.
【点评】本题考查了平行四边形的判定与性质.根据面积法求得BC=3AB是解题的关键,另外,注意解题过程中辅助线的作法.
16.(4分)如图是一张矩形纸片ABCD,点E在AC边上,把△DCE沿直线DE折叠,使点C落在对角线BD上的点F处;点G在AB边上,把△DAG沿直线DG折叠,使点A落在线段DF上的点H处.若HF=1,BF=8,则BD= 29 ,矩形ABCD的面积= 420 .
【分析】由折叠的性质得HD=AD,FD=CD,设AD=x,则HD=x,得AB=CD=x+1,BD=x+9,再在Rt△ABD中,由勾股定理得出方程,解方程,即可解决问题.
【解答】解:∵四边形ABCD是矩形,
∴AB=CD,∠A=90°,
由折叠的性质得:HD=AD,FD=CD,
设AD=x,则HD=x,
∴AB=CD=FD=HD+HF=x+1,
∴BD=FD+BF=x+9,
在Rt△ABD中,由勾股定理得:x2+(x+1)2=(x+9)2,
解得:x=20或x=﹣4(舍去),
∴AD=20,AB=21,BD=x+9=29,
∴矩形ABCD的面积=AD•AB=20×21=420,
故答案为:29,420.
【点评】本题考查了翻折变换的性质、矩形的性质以及勾股定理等知识,熟练掌握翻折变换的性质和矩形的性质,由勾股定理得出方程是解题的关键.
三、解答题(本题有7小题,共66分)
17.(6分)△ABC的周长为12,AC=2AB,设AB=x,BC=y.
(1)求y关于x的函数表达式,并写出自变量x的取值范围;
(2)若△ABC是等腰三角形,求它的三边长.
【分析】(1)隔绝三角形的周长公式解答即可;
(2)根据等腰三角形的性质解答即可.
【解答】解:(1)∵△ABC的周长为12,AC=2AB,设AB=x,BC=y,
∴x+2x+y=12,
∴y=12﹣3x,
∵,
解得:2<x<3,
∴y关于x的函数表达式为:y=12﹣3x(2<x<3);
(2)∵△ABC是等腰三角形,
当x=y时,12﹣3x=x,
解得:x=3,
∴三角形三边为:3,3,6,
∵3+3=6,
∴不能组成三角形,
当2x=y时,12﹣3x=2x,
解得:x=2.4,
∴三角形三边为4.8,4.8,2.4,
∵2.4+4.8>4.8,
∴能组成三角形,
综上所述,三角形的三边为4.8,4.8,2.4.
【点评】此题考查等腰三角形的性质,关键是根据等腰三角形的性质和三角形三边关系得出不等式解答.
18.(8分)关于x,y的方程组,若2<x﹣y<4,则k的取值范围是多少?
【分析】将两个方程相减,整理可得x﹣y=k﹣1,结合2<x﹣y<4得出关于k的不等式组,解之可得.
【解答】解:将两个方程相减可得2x﹣2y=2k﹣2,
即x﹣y=k﹣1,
∵2<x﹣y<4,
∴2<k﹣1<4,
解得:3<k<5.
【点评】本题考查的是解一元一次不等式组,解答此题的关键是把原方程组变形,用k表示出x﹣y的值,再根据x﹣y的取值范围得到关于k的一元一次不等式组,解此不等式组即可求出k的取值范围.
19.(8分)已知一元二次方程(k﹣2)x2﹣4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
【分析】(1)根据一元二次方程的定义结合根的判别式即可得出关于k的一元一次不等式组,解不等式组即可求出k的值;
(2)结合(1)找出k的值,利用分解因式法求出方程x2﹣4x+k=0的根,再将x的值代入x2+mx﹣1=0中即可求出m的值.
【解答】解:(1)∵一元二次方程(k﹣2)x2﹣4x+2=0有两个不相等的实数根,
∴,
解得:k<4且k≠2.
(2)结合(1)可知k=3,
∴方程x2﹣4x+k=x2﹣4x+3=(x﹣1)(x﹣3)=0,
解得:x1=1,x2=3.
当x=1时,有1+m﹣1=0,解得:m=0;
当x=3时,有9+3m﹣1=0,解得:m=﹣.
故m的值为0或﹣.
【点评】本题考查了根的判别式、因式分解法解一元二次方程以及解一元一次不等式组,根据根的判别式得出不等式(或不等式组)是解题的关键
20.(10分)设一次函数y1=kx﹣2k(k是常数,且k≠0).
(1)若函数y1的图象经过点(﹣1,5),求函数y1的表达式.
(2)已知点P(x1,m)和Q(﹣3,n)在函数y1的图象上,若m>n,求x1的取值范围.
(3)若一次函数y2=ax+b(a≠0)的图象与y1的图象始终经过同一定点,探究实数a,b满足的关系式.
【分析】(1)根据待定系数法,可得函数解析式;
(2)根据一次函数的性质,可得答案;
(3)根据函数图象上的点满足函数解析式,可得答案.
【解答】解:(1)∵函数y1的图象经过点(﹣1,5),
∴5=﹣k﹣2k,
解得k=﹣,
函数y1的表达式y=﹣x+;
(2)当k<0时,若m>n,则x1<﹣3;
当k>0时,若m>n,则x1>﹣3;
(3)∵y1=kx﹣2k=k(x﹣2),
∴函数y1的图象经过定点(2,0),
当y2=ax+b经过(2,0)时,0=2a+b,即2a+b=0.
【点评】本题考查了一次函数图象上点的坐标特征,解(1)的关键是利用待定系数法;解(2)的关键是利用一次函数的性质,要分类讨论,以防遗漏;解(3)的关键是理解题意,并求出y1的必过点.
21.(10分)如图,ABCD是矩形纸片,翻折∠B,∠D,使BC,AD恰好落在AC上.设F,H分别是B,D落在AC上的两点,E,G分别是折痕CE,AG与AB,CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
【分析】(1)根据:两组对边分别平行的四边形是平行四边形,证明AG∥CE,AE∥CG即可;
(2)解法1:在Rt△AEF中,运用勾股定理可将EF的长求出;
解法2,通过△AEF∽△ACB,可将线段EF的长求出.
【解答】(1)证明:在矩形ABCD中,
∵AD∥BC,
∴∠DAC=∠BCA.
由题意,得∠GAH=∠DAC,∠ECF=∠BCA.
∴∠GAH=∠ECF,
∴AG∥CE.
又∵AE∥CG,
∴四边形AECG是平行四边形.
(2)解法1:在Rt△ABC中,
∵AB=4,BC=3,
∴AC=5.
∵CF=CB=3,
∴AF=2.
在Rt△AEF中,
设EF=x,则AE=4﹣x.
根据勾股定理,得AE2=AF2+EF2,
即(4﹣x)2=22+x2.
解得x=,即线段EF长为cm;
解法2:
∵∠AFE=∠B=90°,∠FAE=∠BAC,
∴△AEF∽△ACB,
∴.
∴,
解得,即线段EF长为cm;
解法3:
,
即,
解得,即线段EF长为cm.
【点评】本题考查图形的折叠变化,关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
22.(12分)在直角坐标系中,设反比例函数与一次函数y2=k2x+b(k2≠0)的图象都经过点A和点B,点A的坐标为(1,m),点B的坐标为(﹣2,﹣2).
(1)求m的值和一次函数y2的表达式.
(2)当y1>y2时,直接写出x的取值范围.
(3)把函数y2的图象向下平移n(n>0)个单位后,与函数y1的图象交于点(p1,q1)和(p2,q2),当p1=﹣1时,求此时n及p2×q2的值.
【分析】(1)由B的坐标求得反比例函数的解析式进而求得m的值,然后利用待定系数法即可求得一次函数y2的表达式;
(2)根据图象即可求得;
(3)根据反比例函数图象上点的坐标特征,求得q1=﹣4,由y=2x+2﹣n过点(﹣1,﹣4),即可求得n=4,根据反比例函数图象上点的坐标特征即可求得p2×q2=4.
【解答】解:(1)∵反比例函数过点A(1,m),点B(﹣2,﹣2).
∴k1=1×m=﹣2×(﹣2),
∴m=4,k1=4,
∴A(1,4),
把A、B的坐标代入y2=k2x+b(k2≠0)得,
解得,
∴一次函数y2的表达式为y2=2x+2;
(2)观察图象,当y1>y2时,x的取值范围x<﹣2或0<x<1;
(3)由(1)可知y1=,
把点(﹣1,q1)代入得,q1=﹣4,
∴函数y2的图象向下平移n(n>0)个单位后,与函数y1的图象交于点(﹣1,﹣4)和(p2,q2),
∵把函数y2的图象向下平移n(n>0)个单位后得到y=2x+2﹣n,且过点(﹣1,﹣4),
∴﹣4=﹣2+2﹣n,
∴n=4,
∵点(p2,q2)在反比例函数y1=的图象上,
∴p2×q2=4.
【点评】本题是反比例函数与一次函数的交点问题,考查了待定系数法求函数的解析式,函数图象上点的坐标特征,一次函数图象与几何变换,求得交点坐标是解题的关键.
23.(12分)在正方形ABCD中,对角线AC与BD相交于点O,点E是线段OC上的动点.
(1)如图1,若DE平分∠CDO.
①求证:AD=AE.
②若CE=2,求OE的长.
(2)如图2,延长DE交BC于点F连接OF.当DF=2OF时,探究CF与AD的数量关系,并说明理由.
【分析】(1)①由正方形的性质证出∠ADB=∠ACD=45°,由角平分线的性质得出∠ODE=∠CDE,则可得出结论;
②过点E作EF⊥CD于点F,由等腰直角三角形的性质及角平分线的性质可得出结论;
(2)取DF的中点M,连接OM,CM,由三角形中位线定理得出OM=BF,OM∥BF,证明四边形OFCM为平行四边形,由平行四边形的性质得出OM=CF,则可得出结论.
【解答】(1)①证明:∵四边形ABCD是正方形,
∴∠ADB=∠ACD=45°,
∵DE平分∠BDC,
∴∠ODE=∠CDE,
∵∠DEA=∠EDC+∠ACD=45°+∠EDC,∠ADE=∠ADB+∠ODE=45°+∠ODE,
∴∠DEA=∠ADE,
∴AD=AE;
②过点E作EF⊥CD于点F,
∵∠ACD=45°,∠EFC=90°,
∴∠CEF=45°,
∴EF=CF,
∵CE=2,
∴EF=CE=,
∵DE平分∠CDO,EF⊥CD,∠DOE=90°,
∴OE=EF=;
(2)AD=3CF,
理由:取DF的中点M,连接OM,CM,
∵四边形ABCD是正方形,
∴OB=OD,∠DCB=90°,
∵M为DF的中点,
∴OM为△DBF的中位线,
∴OM=BF,OM∥BF,
在Rt△DCF中,DM=MF,
∴CM=MF=DM=DF,
又∵DF=2OF,
∴CM=OF,
∴OF=MF,
∴∠FOM=∠FMO,∠MFC=∠MCF,
∵OM∥CF,
∴∠OMF=∠MFC,
∴∠OFM=∠FMC,
∴OF∥CM,
又∵OF=CM,
∴四边形OFCM为平行四边形,
∴OM=CF,
∵BC=BF+CF=2OM+CF=2CF+CF=3CF,
∴AD=3CF.
【点评】本题属于四边形综合题,考查了正方形的性质,平行四边形的判定与性质,全等三角形的判定和性质,三角形中位线定理,等腰直角三角形的性质和判定等知识,解题的关键是学会添加常用辅助线,构造平行四边形解决问题.
浙江省杭州市西湖区西溪中学2023-2024学年九年级上学期期中数学试题(解析版): 这是一份浙江省杭州市西湖区西溪中学2023-2024学年九年级上学期期中数学试题(解析版),共21页。试卷主要包含了本试卷分试题卷和答题卷两部分等内容,欢迎下载使用。
浙江省杭州市西湖区西溪中学2023-2024学年八年级上学期期中数学试卷: 这是一份浙江省杭州市西湖区西溪中学2023-2024学年八年级上学期期中数学试卷,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙江省杭州市西湖区西溪中学2022-2023学年七年级下学期期中数学试卷: 这是一份浙江省杭州市西湖区西溪中学2022-2023学年七年级下学期期中数学试卷,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












