专题2.8切线长定理-2021-2022学年九年级数学上册同步培优题典【苏科版】

这是一份专题2.8切线长定理-2021-2022学年九年级数学上册同步培优题典【苏科版】，文件包含专题28切线长定理-2021-2022学年九年级数学上册尖子生同步培优题典解析版苏科版docx、专题28切线长定理-2021-2022学年九年级数学上册尖子生同步培优题典原卷版苏科版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

2021-2022学年九年级数学上册尖子生同步培优题典【苏科版】
专题2.8 切线长定理
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题，选择10道，填空8道，解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2021·江苏无锡市·九年级专题练习）如图，P为O外一点，PA、PB分别切O于点A、B，CD切O于点E且分别交PA、PB于点C，D，若PA=4，则△PCD的周长为( )

A．5 B．7 C．8 D．10
【答案】C
【分析】根据切线长定理求解即可
【解析】∵PA、PB分别切O于点A、B，CD切O于点E，PA=4，
∴PA=PB=4，AC=CE，BD=DE，
∴△PCD的周长为PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=4+4=8，
故选：C．
2．（2020·常州市第二十四中学九年级月考）如图PA、PB是圆O的切线，切点分别为A、B，点C在AB上，过C作圆O的切线分别交PA、PB于点D、E，连接OD、OE，若∠P=50°，则∠DOE的度数为（　　　）

A．130° B．50° C．60° D．65°
【答案】D
【分析】连接OA、OB、OC，由切线性质得OB⊥PB、OA⊥PA，从而求得∠AOB的度数，再由切线长定理得到DB=DC，从而证得OD平分∠BOC，同理得OE平分∠AOC，最后由∠DOE=∠AOB得到∠DOE的度数．
【解析】如下图

连OA、OB、OC
∵PB切⊙O于B，PA切⊙O于A
∴OB⊥PB，OA⊥PA
又∠P=50°
∴∠AOB=130°
∵DB切⊙O于B，DE切⊙O于C
∴DB=DC且OC⊥DC
∴OD平分∠BOC，即∠DOC=∠BOC
同理得∠EOC=∠AOC
∴∠DOE=∠DOC+∠EOC
=∠BOC+∠AOC
=(∠BOC+∠AOC)
=∠AOB=×130°
=65°．
故选：D．
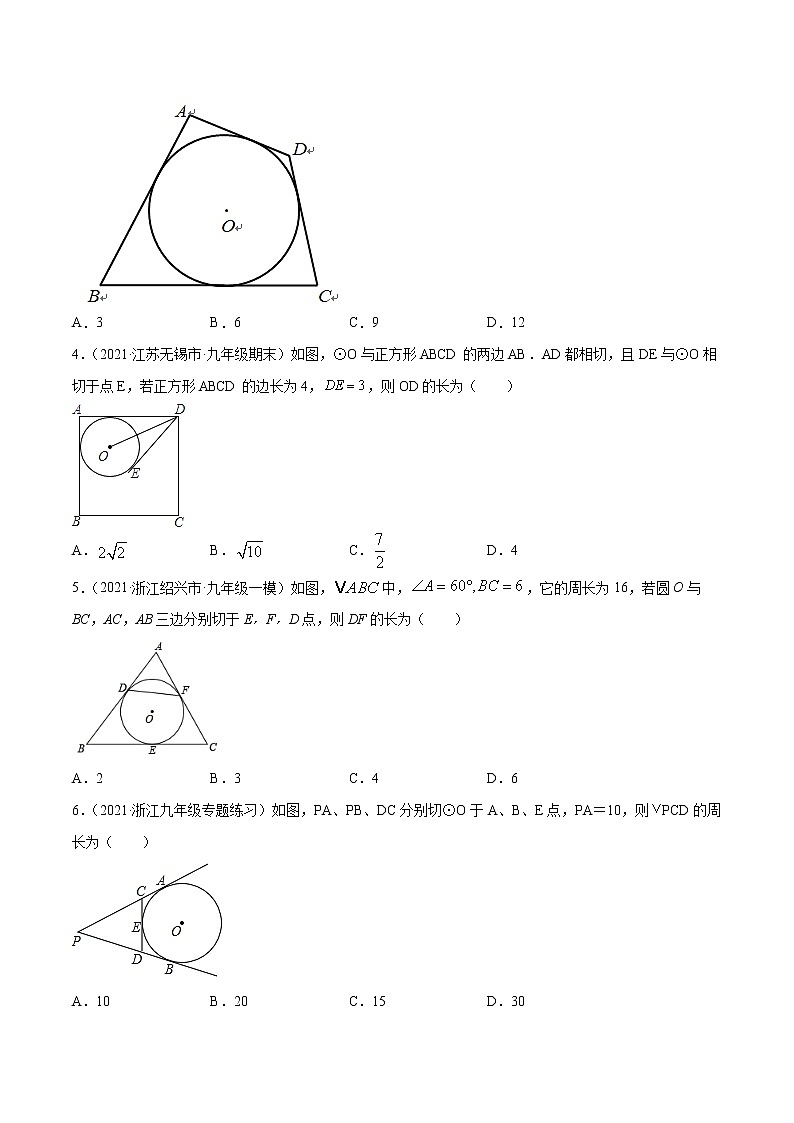
3．（2020·江苏南京市·九年级月考）如图，AB、BC、CD、DA都是⊙O的切线．已知AD＝3，BC＝6，则AB＋CD的值是( )

A．3 B．6 C．9 D．12
【答案】C
【分析】根据切线长定理，可以等到等量关系，AE=AF，BE=BH，DF=DG，CG=CH，又根据题目中已知AD=3，BC=6，从而进行等量替换计算出AB+CD的长度．
【解析】∵AB、BC、CD、DA都是的切线，
∴可以假设切点分别为E、H、G、F，如图所示
∴AE=AF，BE=BH，DF=DG，CG=CH
∴AB+CD=AE+BE+DG+CG=AF+BH+DF+CH=AD+BC
∵AD=3，BC=6
∴AB+CD=3+6=9
故本题最后答案选C．

4．（2021·江苏无锡市·九年级期末）如图，⊙O与正方形ABCD的两边AB．AD都相切，且DE与⊙O相切于点E，若正方形ABCD的边长为4，，则OD的长为（ ）

A． B． C． D．4
【答案】B
【分析】设⊙O与AB、AD相切于点M、N．连接OM、ON，证明四边形AMON是正方形．根据切线长定理，可得DE=DN=3，从而求解 再根据勾股定理计算即可；
【解析】设⊙O与AB、AD相切于点M、N．连接OM、ON，

正方形ABCD,

四边形AMON是正方形．


∵DE、DA是⊙O的切线，
∴DE=DN=3，
∵
∴
在Rt△OND中，
故选：B．
5．（2021·浙江绍兴市·九年级一模）如图，中，，它的周长为16，若圆O与BC，AC，AB三边分别切于E，F，D点，则DF的长为（　　）

A．2 B．3 C．4 D．6
【答案】A
【分析】根据切线长定理求出AD=AF，BE=BD，CE=CF，得出等边三角形ADF，推出，根据BC=6，求出BD+CF=6，求出AD+AF=4，即可求出答案．
【解析】∵⊙O与BC，AC，AB三边分别切于E，F，D点，
∴AD=AF，BE=BD，CE=CF，
∵BC=BE+CE=6，
∴BD+CF=6，
∵AD=AF，∠A=60°，
∴△ADF是等边三角形，
∴AD=AF=DF，
∵AB+AC+BC=16，BC=6，
∴AB+AC=10，
∵BD+CF=6，
∴AD+AF=4，
∵AD=AF=DF，
∴DF=AF=AD=，
故选：A．
6．（2021·浙江九年级专题练习）如图，PA、PB、DC分别切⊙O于A、B、E点，PA＝10，则PCD的周长为（ ）

A．10 B．20 C．15 D．30
【答案】B
【分析】根据切线长定理由PA、PB分别切⊙O于A、B得到PB=PA=10，由于DC与⊙O相切于E，再根据切线长定理得到CA=CE，DE=DB，然后三角形周长的定义得到△PDC的周长=PD+DC+PC=PD+DB+CA+PC，然后用等线段代换后得到三角形PDC的周长等于PA+PB．
【解析】∵PA、PB分别切⊙O于A、B，
∴PB=PA=10，
∵CA与CE为⊙O的切线，
∴CA=CE，
同理得到DE=DB，
∴△PDC的周长=PD+DC+PC=PD+DB+CA+PC，
∴△PDC的周长=PA+PB=20，
故选：B．
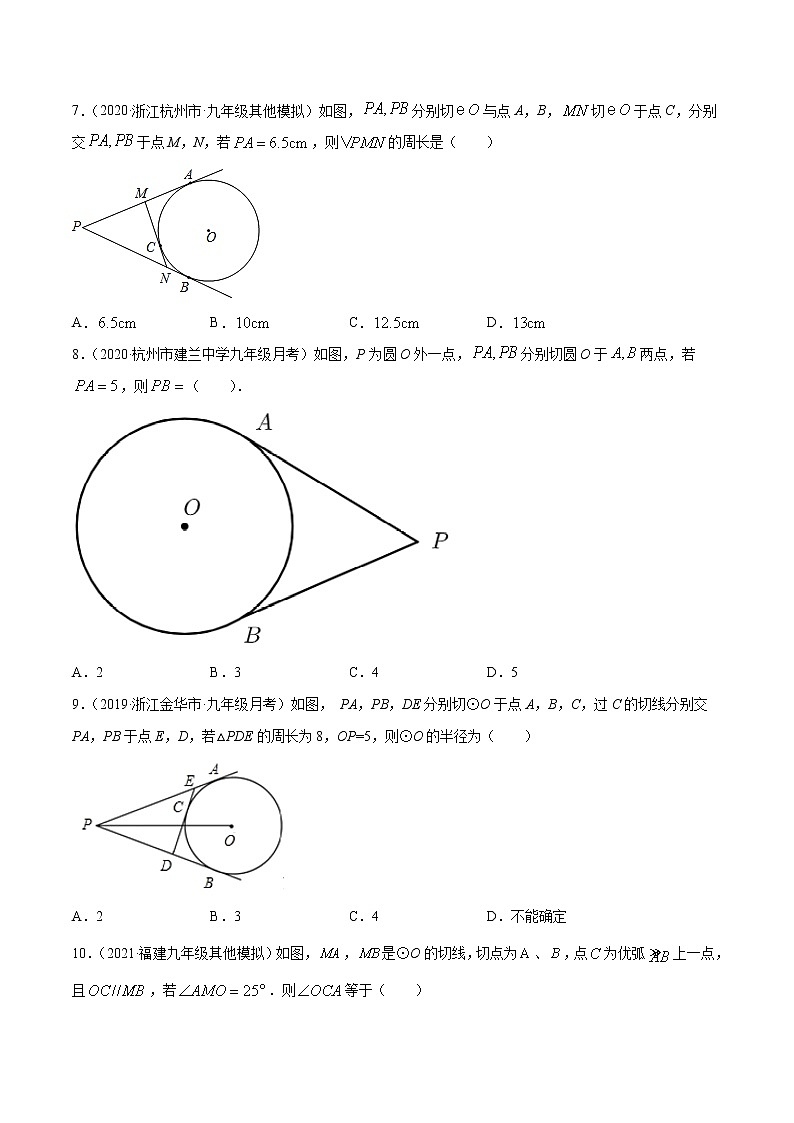
7．（2020·浙江杭州市·九年级其他模拟）如图，分别切与点A，B，切于点C，分别交于点M，N，若，则的周长是（ ）

A． B． C． D．
【答案】D
【分析】利用切线长定理，得，，，即可证明．
【解析】∵分别切与点A，B，
∴，
同理，，
∴．
故选：D．
8．（2020·杭州市建兰中学九年级月考）如图，P为圆O外一点，分别切圆O于两点，若，则（ ）．

A．2 B．3 C．4 D．5
【答案】D
【分析】根据切线长定理直接求得PB=PA=5．
【解析】∵P为圆O外一点，PA，PB分别切圆O于A，B两点，若PA=5，
∴PB=PA=5，
故选：D．
9．（2019·浙江金华市·九年级月考）如图， PA，PB，DE分别切⊙O于点A，B，C，过C的切线分别交PA，PB于点E，D，若△PDE的周长为8，OP=5，则⊙O的半径为（　　）

A．2 B．3 C．4 D．不能确定
【答案】B
【分析】根据切线长定理得BD＝CD，CE＝AE，PA＝PB，由△PDE的周长为8得到AP=BP=4，连接AO，利用勾股定理即可求出AO，即可求解．
【解析】连接OA．

∵PA、PB、DE分别切⊙O于A、B、C点，
∴BD＝CD，CE＝AE，PA＝PB，OA⊥AP．
∴△PDE的周长为2AP＝8
∴AP＝4
在直角三角形OAP中，根据勾股定理，得AO＝=3，
∴⊙O的半径为3．
故选B．
10．（2021·福建九年级其他模拟）如图，，是⊙O的切线，切点为、，点为优弧上一点，且，若．则等于（ ）

A．100° B．15° C．20° D．25°
【答案】C
【分析】如图（见解析），先根据切线长定理可得，再根据平行线的性质可得，然后根据圆的切线的性质可得，从而可得，，最后根据圆周角定理即可得．
【解析】如图，延长交于点，连接，

是的切线，，
，
，
，
又，
，
，
则由圆周角定理得：，
故选：C．
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在横线上）
11．（2021·浙江宁波市·九年级二模）如图，已知在△ABC中，∠C=60°，⊙O是△ABC的外接圆，过点A、B分别作⊙O的切线，两切线交于点P，若⊙O的半径为1，则△PAB的周长为 ____________．

【答案】
【分析】过点A作直径AD，连接BD，则△ABD是直角三角形，且∠ADB=60°，根据三角函数即可求得AB的长，根据切线长定理以及弦切角定理，即可证明△PAB是等边三角形，据此即可求解．
【解析】过点A作直径AD，连接BD，

∵AD是⊙O的直径，
∴∠ABD=90°，
∵∠C=60°，
∴∠ADB=∠C=60°，
∴∠BAD=30°，
∵⊙O的半径为1，
∴AD=2，
∴AB=AD•sin60°=，
∵AP为切线，
∴∠DAP=90°，∠PAB=60°，
又∵AP=BP，
∴△PAB为等边三角形，
∴△PAB的周长=3AB=3．
故答案为：．
12．（2021·江苏九年级一模）如图，、是的切线，、为切点，点、在上．若，则__________．

【答案】
【分析】连接，根据切线长定理得到，根据等腰三角形的性质得到，由圆内接四边形的性质得到，于是得到结论．
【解析】连接，

、是的切线，
，
，
，
，
，
故答案为：．
13．（2021·全国九年级专题练习）如图，从点P引⊙O的切线PA，PB，切点分别为A，B，DE切⊙O于C，交PA，PB于D，E．若△PDE的周长为20cm，则PA=________cm．

【答案】10
【分析】由于PA、PB、DE都是⊙O的切线，可根据切线长定理将△PDE的周长转化为切线PA、PB的长．
【解析】∵PA、PB、DE分别切⊙O于A、B、C，
∴PA=PB，DA=DC，EC=EB；
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=20(cm)；
∴PA=PB=10(cm)，
故答案为10．
14．（2021·湖北襄阳市·九年级一模）PA，PB，CD是⊙O的切线，A，B，E是切点，CD分别交PA，PB于C，D两点，若∠APB=50°，则∠COD的度数为____．
【答案】65°或115°
【分析】根据题意画出符合题意的图形，分别求出∠AOB，再根据切线的性质求出∠COD的度数．
【解析】如图，连接OA、OB、OE
∵PA，PB是⊙O的切线
∴OA⊥AP，OB⊥BP，
∴∠OAP=∠OBP=90°
∵∠APB=50°，
∴∠AOB=360°-90°-90°-50°=130°
∵CD是⊙O的切线
∴OE⊥CD
∵∠CEO=∠DEO=90°
∵PA，PB，CD是⊙O的切线，A，B，E是切点，
∴∠OCA=∠OCE，∠ODB=∠ODE，
∵∠AOC=180°-∠OAC-∠OCA，∠EOC=180°-∠OEC-∠OCE，
∴∠AOC=∠EOC
同理可得∠BOD=∠EOD
∴∠COD=∠EOC+∠EOD=∠AOE+∠BOE=∠AOB=65°

如图，连接OA、OB、OE
同理可得∠AOB=130°
同理可得∠COD=∠EOC+∠EOD=∠AOE+∠BOE
∴∠COD=（360°-130°）=115°
故答案为：65°或115°．


15．（2021·江苏南通市·九年级期末）如图，PA，PB为⊙O的切线，A，B为切点，∠OAB=25°，则∠P=______．

【答案】．
【分析】利用切线长定理可得，由等边对等角得到，，再根据互余的性质解得的度数，最后由三角形内角和180°解题．
【解析】是的切线，为切点，





故答案为：．
16．（2020·江苏苏州市·九年级月考）如图，为外一点，、分别切于、，切于点，分别交，于点、，若的周长为24，的半径是5，则点到圆心的距离______．

【答案】13.
【分析】根据切线长定理和勾股定理即可得到结论．
【解析】、切于、，
；
同理，可得：，；
的周长为24，
∴PC+DC+PD=PC+CD+ED+PD=PA+PB，
，
，
连接，，
，
，
故答案为：13．

17．（2020·江苏泰州市·九年级期中）如图，△ABC的周长为24cm，AC=8cm，⊙O是△ABC的内切圆，⊙O的切线MN与AB、BC分别交于点M、N，则△BMN的周长为____cm．

【答案】8
【分析】根据切线长定理得到AF=AD，DM=MG，GN=NE，AF=AD,CE=CF,BE=BD，然后再利用三角形的周长和BC的长求得AB和BC的长即可．
【解析】∵⊙O是△ABC的内切圆，⊙O的切线MN与AB、BC分别交于点M、N，
∴ AF=AD，DM=MG，GN=NE，AF=AD,CE=CF,BE=BD
∵△ABC的周长为24cm，AC=8cm
∴BD+BE=24-AD-AF-FC-CE=24-(AD+EC) -(AF+FC) =24-2AC=8
∴△BMN的周长为BM+MG+GN+BN=( BM+MD) +(BN+NE)=BD+BE=8．
故答案为8．

18．（2020·南京郑和外国语学校九年级月考）如图，AB、AC 、BD 是⊙O 的切线，P、C、D 为切点，如果 AB=13，BD=3，则 AC的长为____________．

【答案】10
【分析】由于AB、AC、BD是⊙O的切线，则AC=AP，BP=BD，求出BP的长即可求出AC的长．
【解析】为的切线，
，
为的切线，

，
故答案为：10．

三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．（2021·江苏泰州市·泰兴市实验初级中学九年级一模）如图，ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．
（1）求证：∠ACD＝∠B；
（2）若BC＝6，AC＝8，求AD、CD的长．

【答案】（1）见解析；（2）4，
【分析】（1）连接OD，如图，根据切线的性质得到∠ODB＝90°，∠ABC+∠COD＝180°，再根据等角的补角得到∠AOD＝∠ABC，然后根据圆周角定理得到∠AOD＝2∠ACD，从而得到结论；
（2）先利用勾股定理计算出在AB＝10，再利用切线长定理得到BD＝BC＝6，利用线段差可得AD＝4，设⊙O的半径为r，则OD＝OC＝r，OA＝8﹣r，利用勾股定理得到r2+42＝（8﹣r）2，解得r＝3，连接OB交CD于H，如图，则OB垂直平分CD，然后利用面积法可计算出CH，从而得到CD的长．
【解析】（1）证明：连接OD，如图，


∵AB为切线，
∴OD⊥AB，
∴∠ODB＝90°，
∵∠ACB＝90°，
∴∠ABC+∠COD＝180°，
∵∠AOD+∠COD＝180°，
∴∠AOD＝∠ABC，
∵OD=OC，
∴∠OCD＝∠ODC，
∵∠AOD＝∠OCD+∠ODC =2∠ACD，
∴∠ACD＝∠ABC；
（2）在Rt△ABC中，AB＝＝10，
∵OC⊥CB，OC为半径，
∴BC为切线，
∴BD＝BC＝6，
∴AD＝4，
设⊙O的半径为r，则OD＝OC＝r，OA＝8﹣r，
在Rt△AOD中，r2+42＝（8﹣r）2，
解得r＝3，
∴OC＝3，
连接OB交CD于H，如图，
∵OC＝OD，BC＝BD，
∴OB垂直平分CD，
在Rt△OCB中，OB＝，
∵OB•CH＝OC•BC，
∴CH＝，
∴CD＝2CH＝．

20．（2020·江苏苏州市振华中学校九年级月考）如图，，是的切线，、为切点，是的直径，.

（1）求的度数；
（2）当时，求的长.
【答案】（1）；（2）.
【分析】（1）根据切线长定理推出AP=BP，根据等腰三角形性质和三角形的内角和定理求出∠PAB=60°，求出∠PAO=90°即可；
（2）根据直角三角形性质求出OP，根据勾股定理求出AP，根据等边三角形的判定和性质求出即可．
【解析】（1）∵PA，PB是⊙O的切线，
∴AP=BP，
∵∠P=60°，
∴∠PAB=60°，
∵AC是⊙O的直径，
∴∠PAC=90°，
∴∠BAC=90°-60°=30°．
（2）连接OP，则在Rt△AOP中，OA=2，∠APO=30°，
∴OP=4，
由勾股定理得：AP＝2，
∵AP=BP，∠APB=60°，
∴△APB是等边三角形，
∴AB＝AP＝2．

21（2019·泰州市第二中学附属初中九年级三模）如图△ABC中，∠ABC＝90°，CD平分∠ACB交AB于点D，以点D为圆心，BD为半径作⊙D交AB于点E．
（1）求证：⊙D与AC相切；
（2）若AC＝5，BC＝3，试求AE的长．

【答案】（1）见解析；（2）AE＝1．
【分析】（1）过D作DF⊥AC于F，利用角平分线的性质定理可得BD=FD即可证明：⊙D与AC相切；
（2）在直角三角形ABC中由勾股定理可求出AB的长，设圆的半径为x，利用切线长定理可求出CF=BC=3，所以AF=2，AD=4-x，利用勾股定理建立方程求出x，进而求出AE的长．
【解析】（1）证明：过D作DF⊥AC于F，
∵∠B＝90°，
∴AB⊥BC，
∵CD平分∠ACB交AB于点D，
∴BD＝DF，
∴⊙D与AC相切；
（2）设圆的半径为x，
∵∠B＝90°，BC＝3，AC＝5，
∴AB＝＝4，
∵AC，BC，是圆的切线，
∴BC＝CF＝3，
∴AF＝AB﹣CF＝2，
∵AB＝4，
∴AD＝AB﹣BD＝4﹣x，
在Rt△AFD中，（4﹣x）2＝x2+22，
解得：，
∴AE＝4﹣3＝1．

22．（2021·广东汕头市·九年级一模）如图，PA为⊙O的切线，A为切点，过点A作AB⊥OP，垂足为点C，交⊙O于点B，延长BO与PA的延长线交于点D．
（1）求证：PB为⊙O的切线；
（2）若OB=3，OD=5，求OP的长．

【答案】（1）见解析；（2）3
【分析】（1）连接OA，已知AB⊥OP，OB=OA，根据等腰三角形的三线合一的性质可得∠BOP=∠AOP；根据切线的性质定理可得∠OAP=90°，证明△OBP≌△OAP，根据全等三角形的性质可得∠OBP=∠OAP=90°．由此即可证得结论；
（2）在Rt△AOD中，根据勾股定理求得AD=4，由切线长定理可得PA=PB，在Rt△DBP中，根据勾股定理求得PB= 6，再在Rt△OBP中，根据勾股定理求得OP=3．
【解析】（1）证明：连接OA，

∵AB⊥OP，OB=OA，
∴∠BOP=∠AOP，
∵PA是⊙O的切线，
∴∠OAP=90°，
在△OBP与△OAP中，
∴△OBP≌△OAP（SAS），
∴∠OBP=∠OAP=90°．
∴OB⊥PB．
∴PB是⊙O的切线；
（2）∵OD=5，OA=OB=3，∴在Rt△AOD中，AD==4，
∵PA、PB为⊙O的切线，
∴PA=PB，
在Rt△DBP中，PD2=PB2+BD2，即（PB+4）2=PB2+82，
解得，PB= 6，
在Rt△OBP中，OP==3．
23．（2020·安徽合肥市·九年级三模）如图，在中，，以为直径的交于点，的切线交于点，交的延长线于点．

（1）若，，求的半径；
（2）求证：．
【答案】（1）⊙O半径为3；（2）证明见解析．
【分析】（1）连接OE，如图，利用切线的性质得到∠OEF＝90°，设⊙O半径为x，则OB＝OE＝x，在Rt△DEO中利用勾股定理得到x2＋42＝（x＋2）2，然后解方程即可；
（2）连接BE，如图，根据圆周角定理得到∠AEB＝90°，∠CEB＝90°，再利用切线的判断得到BC为⊙O的切线，则根据切线长定理得到BF＝EF，所以∠CBE＝∠BEF，然后证明∠C＝∠CEF得到CF＝EF，从而得到结论．
【解析】（1）连接OE，
∵DE为⊙O的切线，∴90°，
设⊙O半径为x，则，
∵，∴，
在Rt△DEO中，
∴，
解得，即⊙O半径为3；
（2）证明：连接BE，
∵AB为⊙O的直径，
∴90°，90°，
∴90°，90°，
∵在Rt△ABC中，90°，
∴BC为⊙O的切线，
∵DE为⊙O的切线，
∴，
∴，
∴，
∴，
∴．

24．（2021·全国九年级课时练习）如图，在中，，以为直径的⊙O交于点，切线交于点．

（1）求证：；
（2）若，，求的长．
【答案】（1）证明见解析；（2）
【分析】（1）连接，利用切线的性质与已知的直角，结合互余的性质可得答案，
（2）连接，结合（1）问的结论，利用直径所对的圆周角是直角，证明AE=CE，设，利用勾股定理列方程求解即可得到答案．
【解析】（1）证明：连接，
是切线，
，
，
，
，
，
，
．
（2）连接．
，
，
是⊙O的直径，，
是⊙O的切线，
，
，
，
，
在中，，
设，在中，，
在中，，
，
解得，
．