专题2.11圆锥的侧面积-2021-2022学年九年级数学上册同步培优题典【苏科版】

2021-2022学年九年级数学上册尖子生同步培优题典【苏科版】

专题2.11 圆锥的侧面积

姓名：__________________     班级：______________   得分：_________________

注意事项：

本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．

一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．

1．（2021·江苏九年级一模）已知圆锥的底面半径为，母线长为，则这个圆锥的全面积是（    ）

A． B． C． D．

【答案】B

【分析】由于圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长，则可利用扇形的面积公式出圆锥的侧面积，然后把侧面积加上底面积得到它的全面积．

【解析】根据题意，

这个圆锥的全面积．

故选：B．

2．（2021·江苏无锡市·九年级一模）圆锥的高是，其底面圆半径为，则它的侧面展开图的面积为（    ）

A． B． C． D．

【答案】C

【分析】利用勾股定理易得圆锥的母线长，圆锥的侧面积=π×底面半径×母线长，把相应数值代入即可求解．

【解析】∵圆锥的高为4cm，底面半径为3cm，

∴圆锥的母线长为：(cm)，

∴圆锥的侧面展开图的面积为：π×3×5=15π(cm2)．

故选：C．

3．（2021·江苏无锡市·九年级专题练习）如图，沿一条母线将圆锥侧面剪开并展开，得到一个扇形，若圆锥底面半径，扇形圆心解，则该圆锥母线长为（    ）

A．10 B． C．6 D．8

【答案】C

【分析】利用圆锥的侧面展开图为扇形，且这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长以及弧长公式即可列出关于l的方程，解出l即可．

【解析】根据题意得，，

解得，，

即该圆锥母线的长为6．

故选：C．

4．（2021·江苏扬州市·九年级期末）如图，有一块半径为，圆心角为扇形铁皮，要把它做成一个圆锥体容器（接缝忽略不计），那么这个圆锥体容器的高为（    ）

A． B． C． D．

【答案】C

【分析】设做成圆锥之后的底面半径为r，可得，再利用勾股定理即可求解．

【解析】设做成圆锥之后的底面半径为r，

则，

解得，

∴这个圆锥体容器的高为，

故选：C．

5．（2019·江苏连云港市·九年级期末）如图物体由两个圆锥组成，其主视图中，．若上面圆锥的侧面积为1，则下面圆锥的侧面积为（    ）

A．2 B． C． D．

【答案】D

【分析】先证明△ABD为等腰直角三角形得到∠ABD＝45°，BD＝AB，再证明△CBD为等边三角形得到BC＝BD＝AB，利用圆锥的侧面积的计算方法得到上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，从而得到下面圆锥的侧面积．

【解析】∵∠A＝90°，AB＝AD，

∴△ABD为等腰直角三角形，

∴∠ABD＝45°，BD＝AB，

∵∠ABC＝105°，

∴∠CBD＝60°，

而CB＝CD，

∴△CBD为等边三角形，

∴BC＝BD＝AB，

∵上面圆锥与下面圆锥的底面相同，

∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，

∴下面圆锥的侧面积＝×1＝．

故选D．

6．（2020春•锡山区期中）已知圆锥的底面半径为4cm，母线长为5cm，则圆锥的侧面积是（　　）

A．20cm2 B．20πcm2 C．10cm2 D．10πcm2

【分析】利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算即可．

【解析】这个圆锥的侧面积2π×4×5＝20π（cm2）．

故选：B．

7．（2020•通州区一模）若用半径为6，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为（　　）

A．1 B．2 C．3 D．4

【分析】根据弧长公式求出扇形弧长，根据圆的周长公式计算，得到答案．

【解析】扇形的弧长4π，

∴圆锥的底面圆的周长＝4π，

∴圆锥的底面圆半径2，

故选：B．

8．（2020•张家港市模拟）如图，粮仓的顶部是圆锥形状，这个圆锥底面的半径长为3m，母线长为6m，为防止雨水，需在粮仓顶部铺上油毡，如果油毡的市场价是每平方米10元钱，那么购买油毡所需要的费用是（　　）

A．540π元 B．360π元 C．180π元 D．90π元

【分析】圆锥的侧面积＝底面周长×母线长÷2．算出侧面积后乘以单价即可．

【解析】底面半径为3m，则底面周长＝6π，侧面面积6π×6＝18π（m2）．

所需要的费用＝18π×10＝180π（元），

故选：C．

9．（2019秋•海州区校级期末）如图，如果从半径为6cm的圆形纸片上剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的底面半径是（　　）

A．2cm B．4cm C．6cm D．8cm

【分析】易求得扇形的弧长，除以2π即为圆锥的底面半径．

【解析】扇形的弧长为：8πcm，

圆锥的底面半径为：8π÷2π＝4cm，

故选：B．

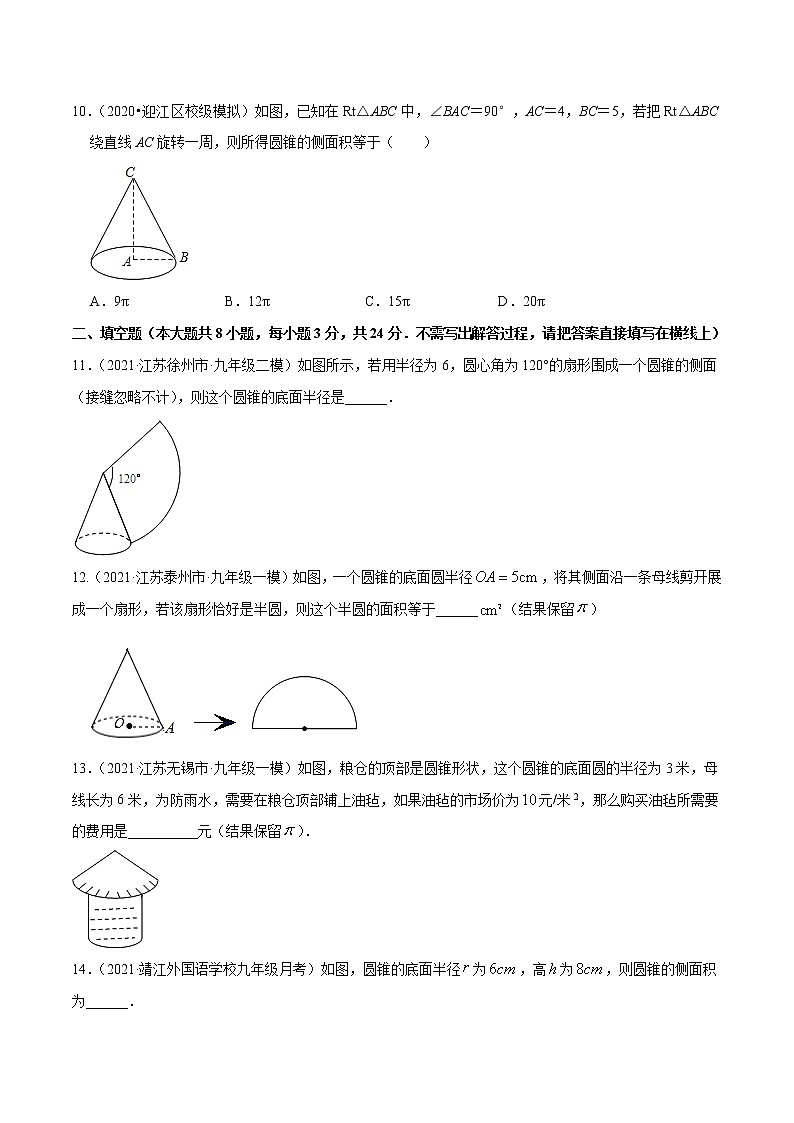
10．（2020•迎江区校级模拟）如图，已知在Rt△ABC中，∠BAC＝90°，AC＝4，BC＝5，若把Rt△ABC绕直线AC旋转一周，则所得圆锥的侧面积等于（　　）

A．9π B．12π C．15π D．20π

【分析】由勾股定理易得圆锥的底面半径长，那么圆锥的侧面积2π×底面半径×母线长，把相应数值代入即可求解．

【解析】∵AC＝4，BC＝5，

∴由勾股定理得：AB＝3

∴底面的周长是：6π

∴圆锥的侧面积等6π×5＝15π，

故选：C．

二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在横线上）

11．（2021·江苏徐州市·九年级二模）如图所示，若用半径为6，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是______．

【答案】2

【分析】根据半径为6，圆心角为120°的扇形弧长，等于圆锥的底面周长，列方程求解即可．

【解析】设圆锥的底面半径为r，

由题意得，，

解得，r=，

故答案为：．

12.（2021·江苏泰州市·九年级一模）如图，一个圆锥的底面圆半径，将其侧面沿一条母线剪开展成一个扇形，若该扇形恰好是半圆，则这个半圆的面积等于______（结果保留）

【答案】

【分析】设展开图的半圆中半径为，易得圆锥的底面周长，也就是侧面展开图的弧长，进而利用弧长公式即可求得圆锥的母线长即展开图中半圆的半径，从而求解．

【解析】设展开图的半圆中半径为

由题意可得，，解得：

∴这个半圆的面积等于

故答案为：．

13．（2021·江苏无锡市·九年级一模）如图，粮仓的顶部是圆锥形状，这个圆锥的底面圆的半径为3米，母线长为6米，为防雨水，需要在粮仓顶部铺上油毡，如果油毡的市场价为元/米2，那么购买油毡所需要的费用是__________元（结果保留）．

【答案】

【分析】根据圆锥侧面积公式，算出油毡的面积，乘以10即可得到结果．

【解析】根据题意得：圆锥侧面积（平方米），

则购买油毡所需要的费用（元）．

故答案为：．

14．（2021·靖江外国语学校九年级月考）如图，圆锥的底面半径为，高为，则圆锥的侧面积为______．

【答案】60πcm2

【分析】首先利用勾股定理求出圆锥的母线长，再通过圆锥侧面积公式可以求得结果．

【解析】∵h＝8，r＝6，

可设圆锥母线长为l，

由勾股定理，l10，

圆锥侧面展开图的面积为：S侧2×6π×10＝60π，

所以圆锥的侧面积为60πcm2．

故答案为：60πcm2；

15．（2020•连云港）用一个圆心角为90°，半径为20cm的扇形纸片围成一个圆锥的侧面，这个圆锥的底面圆半径为　　cm．

【分析】设这个圆锥的底面圆半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr，然后解关于r的方程即可．

【解析】设这个圆锥的底面圆半径为r，

根据题意得2πr，

解得r＝5（cm）．

故答案为：5．

16．（2020•吴中区二模）已知圆锥的侧面积为10πcm2，母线长为5cm，则该圆锥的底面半径为　　cm．

【分析】根据圆锥的侧面积和圆锥的母线长求得圆锥的弧长，利用圆锥的侧面展开扇形的弧长等于圆锥的底面周长求得圆锥的底面半径即可．

【解析】∵圆锥的母线长是5cm，侧面积是10πcm2，

∴圆锥的侧面展开扇形的弧长为：l4π，

∵锥的侧面展开扇形的弧长等于圆锥的底面周长，

∴r2cm．

故答案为：2．

17．（2020•江都区二模）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r＝4，扇形的圆心角θ＝120°，则该圆锥母线l的长为　　．

【分析】由于圆锥的侧面展开图为扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．则利用弧长公式得到2π×4，然后解方程即．

【解析】根据题意得2π×4，

解得l＝12．

故答案为12．

18．（2020•徐州模拟）如图，圆锥底面半径为r，母线长为6，其侧面展开图是圆心角为180°的扇形，则r的值为　　．

【分析】根据底面圆周长＝扇形的弧长，构建方程即可解决问题．

【解析】由题意：2πr，

解得r＝3，

故答案为：3．

三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）

19．（2019·扬州市梅岭中学九年级期中）如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作（以下结果保留根号）：

（1）利用网格确定该圆弧所在圆的圆心D点的位置，并写出D点的坐标为　   　；

（2）连接AD、CD，⊙D的半径为　   　，∠ADC的度数为　   　；

（3）若扇形DAC是一个圆锥的侧面展开图，求该圆锥底面半径．

【答案】（1）圆心D点的位置见解析，（2，0）；（2）2， 90°；（3）．

【分析】（1）利用垂径定理可作AB和BC的垂直平分线，两线的交点即为D点，可得出D点坐标；

（2）在△AOD中AO和OD可由坐标得出，利用勾股定理可求得AD和CD，过C作CE⊥x轴于点E，则可证得△OAD≌△EDC，可得∠ADO＝∠DCE，可得∠ADO+∠CDE＝90°，可得到∠ADC的度数；

（3）先求得扇形DAC的面积，设圆锥底面半径为r，利用圆锥侧面展开图的面积＝πr•AD，可求得r．

【解析】（1）如图1，分别作AB、BC的垂直平分线，两线交于点D，

∴D点的坐标为（2，0），

故答案为：（2，0）；

（2）如图2，连接AD、CD，过点C作CE⊥x轴于点E，

则OA＝4，OD＝2，在Rt△AOD中，可求得AD＝，

即⊙D的半径为，

且CE＝2，DE＝4，

∴AO＝DE，OD＝CE，

在△AOD和△DEC中，

，

∴△AOD≌△DEC（SAS），

∴∠OAD＝∠CDE，

∴∠CDE+∠ADO＝90°，

∴∠ADC＝90°，

故答案为；90°；

（3）弧AC的长＝×＝π，

设圆锥底面半径为r则有2πr＝π，解得：r＝，

所以圆锥底面半径为．

20．（2020·常州市第二十四中学九年级月考）如图，在正方形网格中建立平面直角坐标系，一条圆弧经过网格点A（0，4）、B（-4，4）、C（-6，2），请在网格图中进行如下操作：

（1）若该圆弧所在圆的圆心为D，则D点坐标为 _________；

（2）连接AD，CD，则⊙D的半径长为_________（结果保留根号），∠ADC的度数为_______ °

（3）若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面圆的半径长．（结果保留根号）

【答案】（1）（-2，0）；（2），90；（3）

【分析】（1）根据圆是轴对称图形的性质作AB、BC的垂直平分线，两直线交于点D，则点D即为该圆弧所在圆的圆心；

（2）利用勾股定理求出圆的半径，分别求AD、CD、AC的长，利用勾股定理的逆定理证得△ACD是直角三角形，且∠ADC=90°；

（3）设圆锥的底面圆的半径长为，根据题意列得，求解即可．

【解析】（1）分别作AB、BC的垂直平分线，两直线交于点D，

则点D即为该圆弧所在圆的圆心，

由图形可知，点D的坐标为（-2，0），

故答案为：（-2，0）；

（2）圆D的半径长：AD=CD=，

∵AC=，

∴，，

∴，

∴△ACD是直角三角形，且∠ADC=90°；

故答案为：，90；

（3）设圆锥的底面圆的半径长为，

则，

解得．

21．（2020·江苏连云港市·赣榆实验中学九年级期中）如图①，已知圆锥的母线长l=16cm，若以顶点O为中心，将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°．

（1）求圆锥的底面半径；

（2）求圆锥的表面积．

【答案】（1）4（2）．

【分析】（1）根据题意可求出圆锥的底面周长，故可求出圆锥的底面半径；

（2）根据圆锥的表面积特点即可求解．

【解析】（1）圆锥的底面周长C==

设圆锥的底面半径为r，则

解得r=4

故圆锥的底面半径为4；

（2）圆锥的表面积=．

22．（2019秋•五峰县期末）如图所示，已知扇形AOB的半径为6cm，圆心角的度数为120°，若将此扇形围成一个圆锥，则：

（1）求出围成的圆锥的侧面积为多少？

（2）求出该圆锥的底面半径是多少？

【分析】（1）根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算；

（2）根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式计算．

【解析】（1）圆锥的侧面积12π（cm2）；

（2）该圆锥的底面半径为r，

根据题意得2πr，

解得r＝2．

即圆锥的底面半径为2cm．

23．（2019秋•淮安区期中）如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8．

（1）以直线BC为轴，把△ABC旋转一周，求所得圆锥的底面圆周长．

（2）以直线AC为轴，把△ABC旋转一周，求所得圆锥的侧面积；

【分析】（1）易得底面半径为6m，直接利用圆的周长公式求得底面圆的周长即可；

（2）利用勾股定理求得母线的长，然后求得圆锥的侧面积即可．

【解析】（1）2π×6＝12π．

（2）∵∠C＝90°，AC＝6，BC＝8，

∴AB10，

所以以直线AC为轴，把△ABC旋转一周，得到的圆锥的侧面积10×2π×8＝80π；

24．（2019•邵阳）如图，在等腰△ABC中，∠BAC＝120°，AD是∠BAC的角平分线，且AD＝6，以点A为圆心，AD长为半径画弧EF，交AB于点E，交AC于点F．

（1）求由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积；

（2）将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高h．

【分析】（1）利用等腰三角形的性质得到AD⊥BC，BD＝CD，则可计算出BD＝6，然后利用扇形的面积公式，利用由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积＝S△ABC﹣S扇形EAF进行计算；

（2）设圆锥的底面圆的半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2πr，解得r＝2，然后利用勾股定理计算这个圆锥的高h．

【解析】∵在等腰△ABC中，∠BAC＝120°，

∴∠B＝30°，

∵AD是∠BAC的角平分线，

∴AD⊥BC，BD＝CD，

∴BDAD＝6，

∴BC＝2BD＝12，

∴由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积＝S△ABC﹣S扇形EAF6×123612π；

（2）设圆锥的底面圆的半径为r，

根据题意得2πr，解得r＝2，

这个圆锥的高h4．