江苏省扬州市宝应县2021-2022学年八年级下学期期末数学试题(word版含答案)

八年级数学期末试卷

（满分：150分   测试时间：120分钟）

一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）

1．下列是一组logo设计的图案（不考虑颜色），既是轴对称图形又是中心对称图形的是（    ）

A．    B．    C．    D．

2．为了解家长对“禁止学生带手机进入校园”这一规定的意见，某校随机抽取本校100名学生家长进行调查，这一问题中样本的容量是（    ）

A．100                        B．被抽取的100名学生家长

C．全校学生家长的意见         D．被抽取的100名学生家长的意见

3．对于事件“某学习小组14人中至少有2人在同一个月过生日”，从发生的可能性大小判断，你认为该事件属于（    ）

A．不可能事件    B．随机事件    C．必然事件    D．无法判断

4．若二次根式在实数范围内有意义，则x的取值范围是（    ）

A．    B．    C．    D．

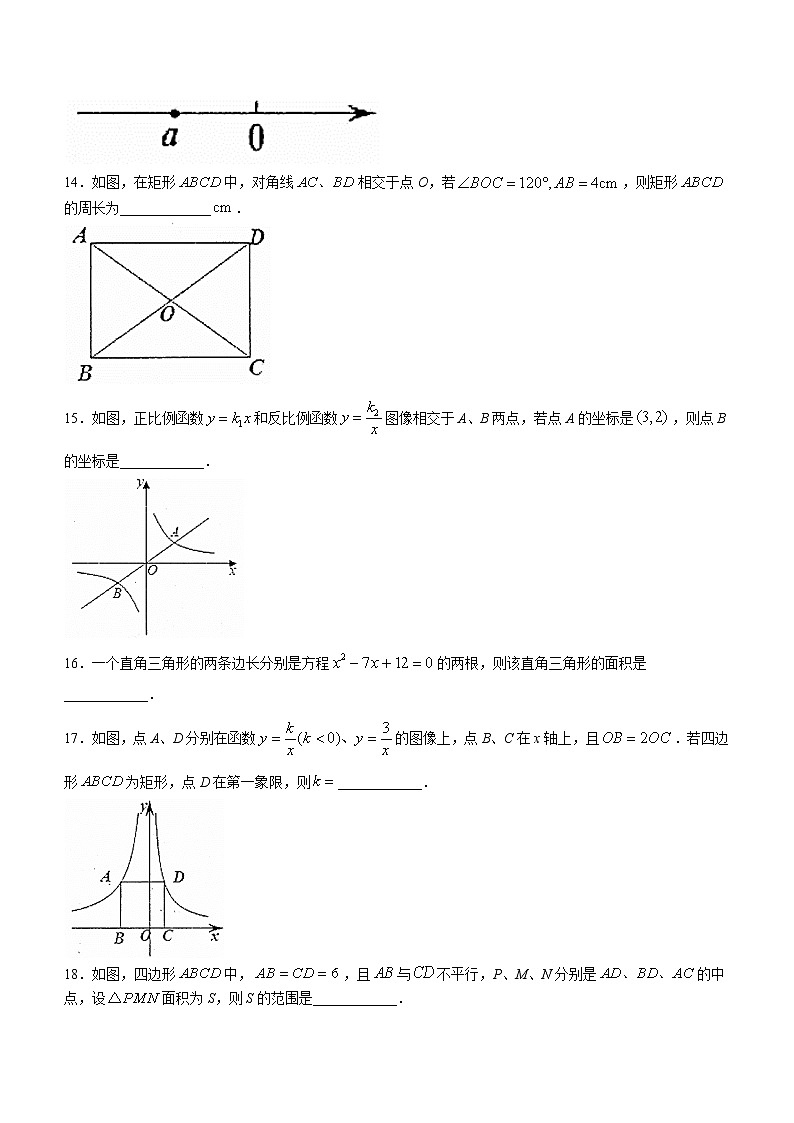
5．关于某个函数表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征．

甲：函数图像经过点；乙：函数图像经过第四象限；丙：当时，y随x的增大而增大．则这个函数表达式可能是（    ）

A．    B．     C．     D．

6．如图，在四边形中，对角线相交于点O，，，，，则四边形的面积为（    ）

A．6    B．12    C．20    D．24

7．如图，设则有（    ）

A．    B．    C．    D．

8．定义新运算“※”：对于实数m、n、p、q，有，其中等式右边是通常的加法和乘法运算，例如：．若关于x的方程有两个实数根，则k的取值范围是（    ）

A．    B．    C．且    D．且

二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）

9．“神舟十四”号载人飞船发射前，工程师对载人飞船和“长征二号F”火箭所有零部件进行检查，应采用的调查方式是____________（请填“普查”或“抽样调查”）．

10．某工厂生产一批足球共10000只，经工厂质检科抽检获得该批足球优等品的频率约为0.975，则这批足球的优等品约为____________只．

11．计算：__________．

12．如图，是等腰直角三角形，是斜边，D为内一点，将绕点A逆时针旋转后与重合，若，那么线段的长等于____________．

13．如图，数轴上点A表示的数为a，化简：____________．

14．如图，在矩形中，对角线相交于点O，若，则矩形的周长为_____________．

15．如图，正比例函数和反比例函数图像相交于A、B两点，若点A的坐标是，则点B的坐标是____________．

16．一个直角三角形的两条边长分别是方程的两根，则该直角三角形的面积是____________．

17．如图，点A、D分别在函数的图像上，点B、C在x轴上，且．若四边形为矩形，点D在第一象限，则____________．

18．如图，四边形中，，且与不平行，P、M、N分别是的中点，设面积为S，则S的范围是____________．

三、解答题（本大题共有9小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

19．（本题8分）化简或计算：

（1）         （2）

20．（本题8分）先化简，再求值：，其中．

21．（本题8分）某学校计划在八年级开设四门劳动实践课程“折扇”、“刺绣”、“剪纸”、“陶艺”，要求每人只能参加其中一门课程，为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调查，并根据调查结果绘制成如图所示的条形统计图和扇形统计图（部分信息未给出），扇形统计图中刺绣部分和折扇部分区域之和刚好是圆的一半．

请你根据以上信息解决下列问题：

（1）参加问卷调查的学生人数为____________人，补全条形统计图（画图并标注相应数据）；

（2）在扇形统计图中，选择“陶艺”课程的学生占____________；

（3）若该校八年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？

22．（本题8分）己知关于x的一元二次方程．

（1）若，求此方程的解；

（2）当时，试判断方程的根的情况．

23．（本题10分）如图，点A、B、D、E在同一条直线上，，，．

（1）求证：．

（2）连结，请判断四边形的形状，并证明你的结论．

24．（本题10分）某地为美化环境，计划种植树木600棵．由于志愿者的加入，实际每天植树的棵树比原计划增加了，结果提前3天完成任务．求实际每天植树多少棵？

25．（本题10分）如图，将一张长方形纸片沿折叠，使C、A两点重合，点D落在点G处．已知，．

（1）求证：是等腰三角形；

（2）求线段的长．

26．（本题10分）通过实验研究发现：初中生听课注意力指标随上课时间的变化而变化，上课开始时，学生注意力逐渐增强，中间一段时间，学生的注意力保持平稳状态，随后开始慢慢下降．学生注意力指标y随时间x（分钟）变化的函数图像如图所示，当和时，图像是线段；当时，图像是双曲线的一部分．

（1）求点A对应的指标值；

（2）张老师在一节课上实践探究活动需要17分钟，他能否经过适当的安排，使学生在实践探究活动时间，注意力指标都不低于36？请说明理由．

27．（本题12分）如图，点A和点是反比例函数图像上的两点，点B在反比例函数的图像上，分别过点A、B作y轴的垂线，垂足分别为点C、D，，连接交y轴于点F．

（1）求k；

（2）设点A的横坐标为a，点F的纵坐标为m，求证：；

（3）连接，当时，求A的坐标．

28．（本题12分）如图1，在正方形中，，点E是的中点，以为边作正方形，连接．将正方形绕点D顺时针旋转，旋转角为．

（1）如图2，在旋转过程中，判断与是否全等，并说明理由；

（2）如图3，延长交直线于点P．

①求证：；

②在旋转过程中，线段的长度是否存在最大值？若存在，求出最大值；若不存在，请说明理由．

八年级数学期末试卷参考答案和评分建议202206

一、选择题

二、填空题

9、普查    10、9750    11、4    12、    13、0    14、

15、    16、6或    17、    18、

三、解答题

19．（1）原式

（2）原式

20、原式

当时，原式

21、解：（1）50（名），补全统计图如下：

（2）10；

（3）（名），

答：选择“刺绣”课程的学生有200名．

22、解：（1）当时，方程为

∴

∴

∴

∴

∴

（2）由一元二次方程得，

∴

∵

∴，

∴此时该方程总有两个实数根．

23、（1）证明：∵

∴

在和中，

∴．

（2）结论：四边形是

∵

∴，

∴

∴四边形是

24、解：设原计划每天植树x棵，则实际每天植树棵，

依题意得：，

解得：，

经检验，是原方程的解，且符合题意，

∴．

答：实际每天植树50棵．

25、（1）证明：由折叠性质可知，，

∵四边形是矩形

∴，

∴，

∴．

∴，

∴为等腰三角形．

（2）解：由折叠可得，设，

则，

∵，

在中，有，

即，解得：．

由（1）结论可得，

故．

26、解：（1）设当时，反比例函数的解析式为，

将代入得：，

解得，

∴反比例函数的解析式为，

当时，，∴，

∴，即A对应的指标值为20；

（2）设当时，的解析式为，

将代入得：，

解得，

∴的解析式为，

当时，，

解得，

由（1）得反比例函数的解析式为，

当时，，

解得，

∴时，注意力指标都不低于36，

而，

∴能经过适当的安#，使学生在听这道综合题的讲解时，注意力指标都不低于36．

27、解：（1）点是反比例函数图象上的点，

∴，

解得，

（2）在和中，

，

∴，

∴，

即，

整理得；

（3）设A点坐标为，

则，

∵，

∴，

即，

解得（舍去）或，

∴A点的坐标为．

28、解：（1）如图2中，结论：．

证明：∵四边形是正方形，

∴，，

∵，，

∴，

∴，

∴．．

（2）①证明：如图3中，设交于O．

∵，

∴，

∵，，

∴，

∴，

∴．

②∵，是定值，

∴当最小时，的值最大，

∴当时，的值最小，此时的值最大，此时点F与P重合（如图4中），

∵，

∴，

∵，

∴，

∴的最大值为．