山西省临汾市部分区县2021-2022学年八年级下学期期末调研测试数学试卷(含答案)

山西省2021～2022学年八年级下学期期末评估卷

一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求）

1. 对于函数y=x+1，自变量x取5时，对应的函数值为（    ）

A. 3 B. 36 C. 16 D. 6

2. 一次函数y=5x－10图象与正比例函数y=x的图象的交点是（    ）

A.  B.  C.  D. （1，1）

3. 下列说法正确的是（    ）

A. 有一个角是直角的平行四边形是正方形

B. 对角线相等的四边形是正方形

C. 四边都相等的四边形是菱形

D. 对角线互相垂直的四边形是矩形

4. 山西某中学初二年级有7个班，期中考试数学成绩为优秀（90分以上）的学生人数分别为6，8，10，2，8，5，7，则这组数的中位数是（    ）

A. 5 B. 6 C. 7 D. 6.5

5. 山西某煤矿一个水池存有1000L水，现在水泵以每分钟抽水20L的速度把水池的水抽出，下图能近似的表示水池剩余水量y与抽水时间x的关系的是（    ）

A.  B.  C.  D.

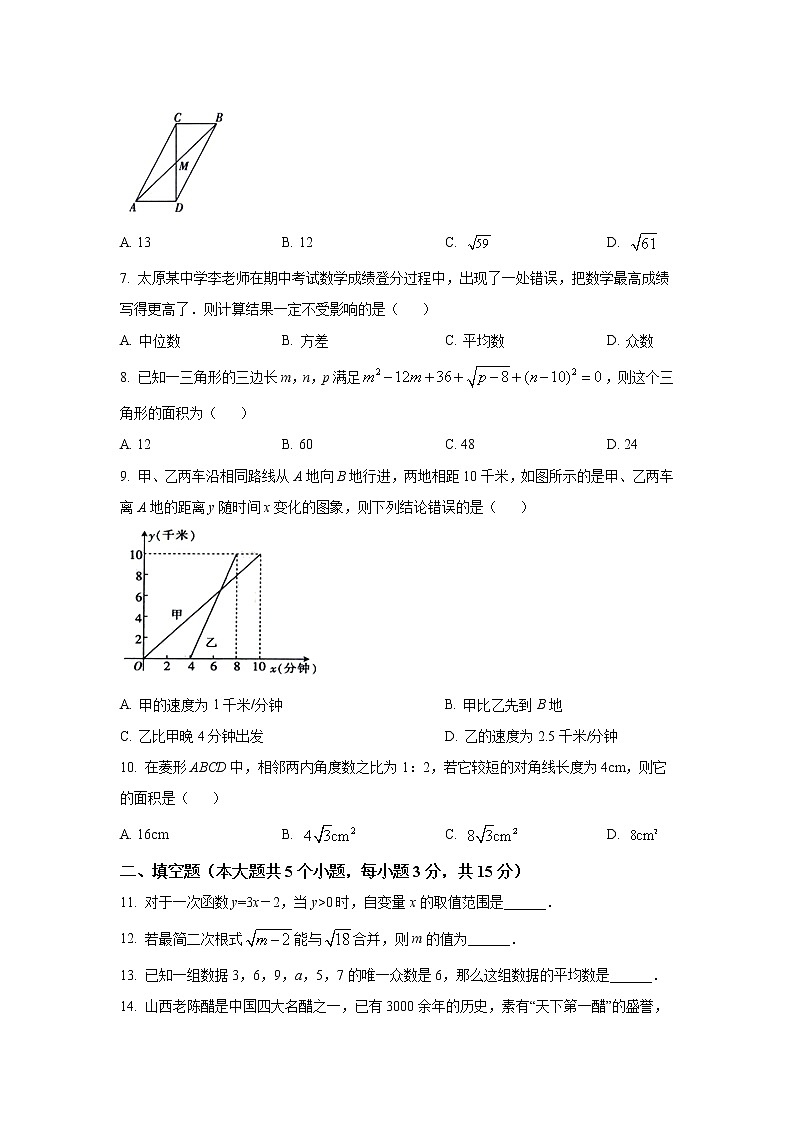
6. 如图，在平行四边形ACBD中，对角线CD⊥AD，且与另一条对角线AB相交于点M，若AD，AC边长分别为5和13，则MB长为（    ）

A. 13 B. 12 C.  D.

7. 太原某中学李老师在期中考试数学成绩登分过程中，出现了一处错误，把数学最高成绩写得更高了．则计算结果一定不受影响的是（    ）

A. 中位数 B. 方差 C. 平均数 D. 众数

8. 已知一三角形的三边长m，n，p满足，则这个三角形的面积为（    ）

A. 12 B. 60 C. 48 D. 24

9. 甲、乙两车沿相同路线从A地向B地行进，两地相距10千米，如图所示的是甲、乙两车离A地的距离y随时间x变化的图象，则下列结论错误的是（    ）

A. 甲的速度为1千米/分钟 B. 甲比乙先到B地

C. 乙比甲晚4分钟出发 D. 乙的速度为2.5千米/分钟

10. 在菱形ABCD中，相邻两内角度数之比为1：2，若它较短的对角线长度为4cm，则它的面积是（    ）

A. 16cm B.  C.  D.

二、填空题（本大题共5个小题，每小题3分，共15分）

11. 对于一次函数y=3x－2，当y>0时，自变量x的取值范围是______．

12. 若最简二次根式能与合并，则m的值为______．

13. 已知一组数据3，6，9，a，5，7的唯一众数是6，那么这组数据的平均数是______．

14. 山西老陈醋是中国四大名醋之一，已有3000余年的历史，素有“天下第一醋”的盛誉，以色、香、醇、浓、酸五大特征著称于世．某粮油店销售一种山西老陈醋，标价每瓶70元（10斤装），店里有个团购优惠，团购老陈醋5瓶以上，超过部分可享受8折优惠，若康康和朋友一起团购了x（x>5）瓶老陈醋共付款y元，则y与x的函数关系式为______．

15. 一张矩形MNPQ纸片按如图所示的方式折叠，使得顶点Q与N重合，折痕为AB，MN=3，MQ=9，则折痕AB的长度为______．

三、解答题（本大题共8个小题，共75分．解答应写出文字说明，证明过程或演算步骤）

16. （1）计算：．

（2）下面是夏红同学对题目的计算过程，请认真阅读并完成相应的任务．

题目：已知，求的值．

原式第一步

　　　　　第二步

　　　　　　　　第三步

所代入上式，得

原式　　　　　第四步

　　　第五步

．　　　　　　　　第六步

任务一：填空：

①在化简步骤中，第______步是进行分式的通分．

②第_____步开始出错，这一错误的原因是______．

任务二：请直接写出该题计算后的正确结果．

17. 如图，小明在甲岛上的一个观测站A处观测，发现在甲岛的正西方10海里处B点有一艘船向正北方驶去，2小时后，小明再次观察发现该船位于距离甲岛海里的C处，求该船的行驶速度．

18. 已知四边形ABCD，//，AD=DC=10，DB平分∠ADC，BD=12，求四边形ABCD的面积．

19. 山西某中学王老师为了选拔一名优秀的学生参加市内的数学比赛，对两名备赛选手进行了6次测验，两位同学的测验成绩如表所示：

（参考公式）

根据表中提供的数据，解答下列问题：

（1）a值为______，d的值为______．

（2）求b和c的值，并直接指出哪位同学的成绩更稳定．

（3）根据以上信息，你认王老师应该选哪位同学参加比赛，请说明理由．

20. 阅读与思考

若两个等腰三角形有公共腰，则称这两个等腰三角形不在公共腰上的两个顶点关于腰互为对顶点．若再满足不在公共腰上的两个角的和是90°，则称这两个顶点关于腰为互余对顶点．

如图1，在四边形ABCD中，AC是一条对角线，CD=CA=CB，则点B与点D关于AC互为对顶点，若再满足∠B+∠D=90°，则点B与点D关于AC为互余对顶点．

任务：

如图2，平行四边形ABCD与四边形ABCE有两边重合，AC为两个四边形的对角线，AE=AD=AC，∠ACB=70°．

（1）证明：点B与点E关于AC互为对顶点．

（2）当点B与点E关于AC为互余对顶点时，求∠DCE的度数．

21. 嘎啦苹果和油桃是运城特产水果，运城某水果经销店每天从农场购进嘎啦苹果和油桃进行销售，两种水果的进价和售价如下：

水果经销店花费1300元购进运城油桃的数量是花费400元购进嘎啦苹果的数量的两倍．

（1）求每斤嘎啦苹果和每斤运城油桃的进价．

（2）水果经销店每天购进这两种水果共200斤，其中嘎啦苹果不少于100斤且不超过130斤，并在当天都销售完．设每天销售嘎啦苹果x斤，当天销售这两种水果总获利W元（销售过程中损耗不计）．求出W与x的函数关系式，并确定当天销售这两种水果的最大利润．

22. 综合与实践

已知线段AD向下平移m个单位后，再向右平移n个单位至线段BC，点A，D的对应点分别为点B、C，连接AB、CD、AC、BD，AC与BD交于O点．

（1）如图1，求证：OB=OD．

（2）如图2，过D点作DM⊥BC于M，N为CD的中点，连接MN，若∠ADB=45°，，MN=4，求的值．

（3）在（2）条件下，H在BC上移动，当为等腰三角形时，请直接写出HC的长．

23. 如图，过A（0，6），B（6，0）两点的直线与直线y=x交于点F，平行于y轴的直线l从y轴出发，以每秒0.5个单位长度的速度沿x轴向右平移，到达F点时停止．直线l分别与AB，OF交于点C、D．以CD为斜边向左侧作等腰直角三角形，设与重叠部分图形的周长为p，直线l的运动时间为t秒．

（1）求直线AB的解析式及点F的坐标．

（2）当点E落在y轴上时，求p的值．

（3）试探究当直线l从y轴出发，向右移动过程中，p与t的函数关系式（直线l在y轴上与经过F点的两种情况不考虑）．

参考答案

1. 【答案】D
2. 【答案】A
3. 【答案】C
4. 【答案】C
5. 【答案】B
6. 【答案】D
7. 【答案】A
8. 【答案】D
9. 【答案】B
10. 【答案】C
11. 【答案】
12. 【答案】4
13. 【答案】6
14. 【答案】
15. 【答案】
16. 【答案】（1）10；（2）任务一：①一；②五，分子没有乘；任务二：．

【详解】（1）原式=6+5－1=10．

（2）任务一：①一．

②五，分子没有乘．

任务二：原式

=．

17. 【答案】该船的行驶速度为7.5海里/小时

【详解】依题意，AB=10海里，海里，

由勾股定理，得（海里），

15÷2=7.5（海里/小时）．

答：该船的行驶速度为7.5海里/小时．

18. 【答案】四边形ABCD的面积为96

【详解】如图，连接AC，交BD于点O．

∵，

∴∠ABD=∠BDC．

∵BD平分∠ADC，

∴∠ADB=∠BDC，

∴∠ABD=∠ADB，

∴AD=AB．

∵AD=CD，

∴AB=CD

∵，

∴四边形ABCD为平行四边形．

∵AD=CD，

∴平行四边形ABCD为菱形，

∴AC⊥BD．

∵AD=10，BD=12，

∴，，

∴．

19. 【答案】（1）85，86   

（2），；乙的成绩更稳定   

（3）选择乙同学．理由：甲乙同学成绩的平均数相同，且乙同学成绩的中位数更大，方差更小，成绩更稳定．

【小问1详解】

甲同学成绩从低到高排序为：80，83，85，85，87，90；

则中位数；

观察乙同学的成绩，出现次数最多的成绩为86，故众数．

【小问2详解】

根据平均数的定义，；

根据题中所给的方差公式，

．

由于甲乙同学成绩的平均数相同，而甲同学成绩的方差大于乙同学成绩的方差，

故乙的成绩更稳定．

【小问3详解】

选择乙同学．

理由：甲乙同学成绩的平均数相同，且乙同学成绩的中位数更大，方差更小，成绩更稳定．

20. 【答案】（1）见解析    （2）∠DCE=20°

【小问1详解】

证明：∵四边形ABCD是平行四边形，

∴AD=CB．

∵AD=AC，

∴CB=AC．

∵AE=AC，

∴点B与点E关于AC互为对顶点．

【小问2详解】

∵CB=AC，∠ACB=70°，

∴∠CAB=∠B=55°．

∵四边形ABCD是平行四边形，

∴∠D=∠B=55°．

∵，

∴∠ACD=∠CAB=55°

∵点B与点E关于AC为互余对顶点，

∴∠E=90°－∠B=35°．

∵AE=AC，

∴∠ACE=∠E=35°，

∴∠DCE=∠ACD－∠ACE=55°－35°=20°．

21. 【答案】（1）每斤嘎啦苹果的进价是4元，每斤运城油桃的进价是6.5元   

（2）当天销售这两种水果的最大利润为450元

【小问1详解】

由题意，得，解得m=4，

经检验，m=4是原分式方程的解．

m+2.5=6.5（元/斤）．

答：每斤嘎啦苹果的进价是4元，每斤运城油桃的进价是6.5元．

【小问2详解】

W=（6－4）x+（9－6.5）（200－x），W=－0.5x+500．

∵－0.5<0，∴W随x增大而减小，

依题意，，

∴当x=100时，W的最大值=－0.5×100+500=450（元），

答：当天销售这两种水果的最大利润为450元．

22. 【答案】（1）见解析    （2）   

（3）HC的长为8或或

【详解】（1）证明：由平移的性质，得，AD=BC，

∴四边形ABCD是平行四边形，∴OB=OD

（2）∵四边形ABCD为平行四边形，

∴∠ADB=∠CBD．，．

∵∠ADB=45°，DM⊥BC，

∴△BDM为等腰直角三角形，∴BM=MD=6．

∵△CMD为直角三角形，N为CD的中点，，∴CD=2MN=8．

在中，由勾股定理，得，∴．

（3）①当HC=DC=8时，如图构成等腰三角形

②当HD=HC时，如图构成等腰三角形

此时设HM为x

∵
 

∴

解得：

∴HC=x+MC=

③当DH=DC时，如图构成等腰三角形：

此时HC=2MC=

故HC长度为：8或或．

23. 【答案】（1）y=－x+6，点F的坐标为（3，3）   

（2）   

（3）

【小问1详解】

设过A（0，6），B（6，0）两点的直线解析式为y=kx+b，

代入点的坐标，得，

解得k=－1，b=6．

故直线AB的解析式为y=－x+6，

联立方程，得，解得，

∴点F的坐标为（3，3）．

【小问2详解】

过点E作EM⊥CD于点M，

设点D的坐标为（a，a），则C（a，6－a）．

∵为等腰直角三角形，

∴

∵点E在y轴上，

∴，

∴，解得，

∴CD=6－2a=3，，

∴．

【小问3详解】

由（2）可知时，点E恰好在y轴上．

当0<t<3时，点E在y轴的左侧，如图，过C作轴于点I，过D作DJ⊥y轴于点J，设CE与y轴相交于点K，DE与y轴相交于点L．

点D坐标为，，CD=6－t．

∵△CED等腰直角三角形，

∴∠CKI=∠ECD=45°

∴，．

同理可得．

∵，

∴，

即．

如图，当3<t<6时，点E在y轴右侧，

∴，

∴

，

即．

综上，