2020-2021学年9.3 分式方程教课内容ppt课件

这是一份2020-2021学年9.3 分式方程教课内容ppt课件，共16页。PPT课件主要包含了分式方程，解得x3，所以原分式方程无解，为什么产生增根，解得x21，整式方程，解整式方程，检验并下结论，解分式方程，随堂练习等内容，欢迎下载使用。
"复兴号"中国标准动车组构建了体系完整、结构合理、先进科学的技术标准体系，动车组基础通用、车体、走行装置、运用维修等10多个方面均达到国际先进水平。为了满足经济高速发展的需求，我国铁路部门不断进行技术革新，提高列车运行速度。已知上海到北京相距1600km，复兴号速度提高25%后，运行时间缩短了4h，你能求出复兴号提速前的速度吗？
像这样，分母中含有未知数的方程叫做分式方程.
以前学过的分母里不含有未知数的方程叫做整式方程.
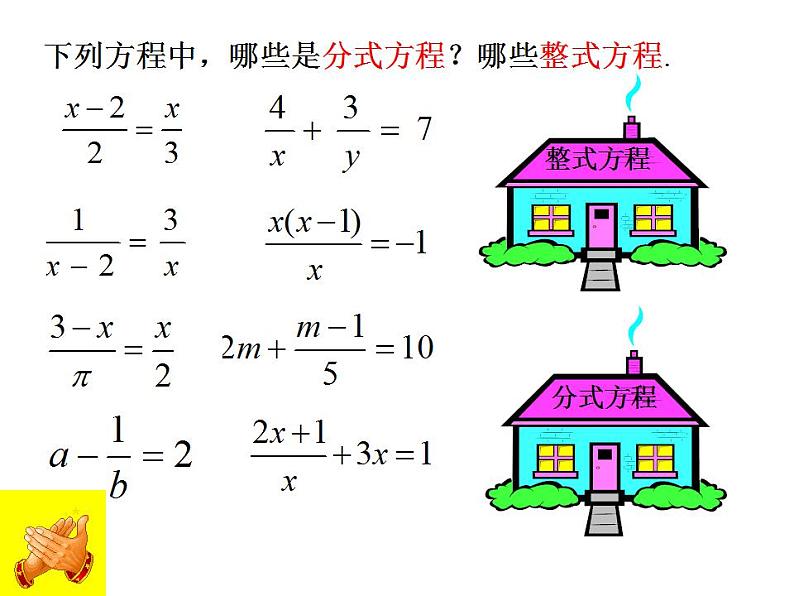
下列方程中，哪些是分式方程？哪些整式方程.
(1)分式方程的特征是什么？
分式方程的特征是分母中含有未知数.
(2)如何解分式方程？
回顾：1.什么是方程的解？　　　2.在解有分母的一元一次方程中怎么去分母？例如：
我们能不能效仿有分母的一元一次方程的解法，想办法去掉分式方程的分母，把它转化成整式方程？
下面我们一起研究下怎么样来解分式方程：
去分母后，分式方程就转变为整式方程了。
所以列车提速前速度为80km/h.
解分式方程的基本思路是将分式方程化为整式方程，具体做法是“去分母”，即方程两边同乘最简公分母，这也是解分式方程的一般思路和做法。
方程两边同乘以最简公分母（x-3），得
检验：将x=3代入原分式方程，发现这时x-3的值为0，相应分式无意义.所以x=3不是原分式方程的解.
x=3是原方程两边同乘以最简公分母变形后的整式方程的根，但不是原分式方程的根，这样的根称之为增根
　　解分式方程时应进行如下检验：将整式方程的解代入最简公分母，如果最简公分母的值不为０，则整式方程的解是原分式方程的解，否则，这个解不是原分式方程的解.
解分式方程，如何检验？
　　在去分母时，两边同乘一个含未知数的整式，是否为０事先不知道，以致导致出现分母为０的现象，因此，解分式方程必须检验.
例1 解分式方程
检验:x=21时，x(x-3) ≠0,所以，x=21是原方程的解．
① ② 　③
1、在方程的两边都乘以最简公分母，约去分母，化成整式方程. 2、解这个整式方程. 3、把整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解，必须舍去. 4、写出原方程的根.