2020-2021学年7.4 三角函数应用多媒体教学ppt课件

这是一份2020-2021学年7.4 三角函数应用多媒体教学ppt课件，文件包含74三角函数应用pptx、74三角函数应用doc等2份课件配套教学资源，其中PPT共55页， 欢迎下载使用。


第7章 三角函数
7.4　三角函数应用
课标要求
1.会用三角函数解决简单的实际问题.2.体会可以利用三角函数构建刻画事物周期变化的数学模型.
素养要求
通过实际问题，构建三角函数数学模型，重点提升学生的数学抽象、数学运算和数学建模素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
内容索引
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
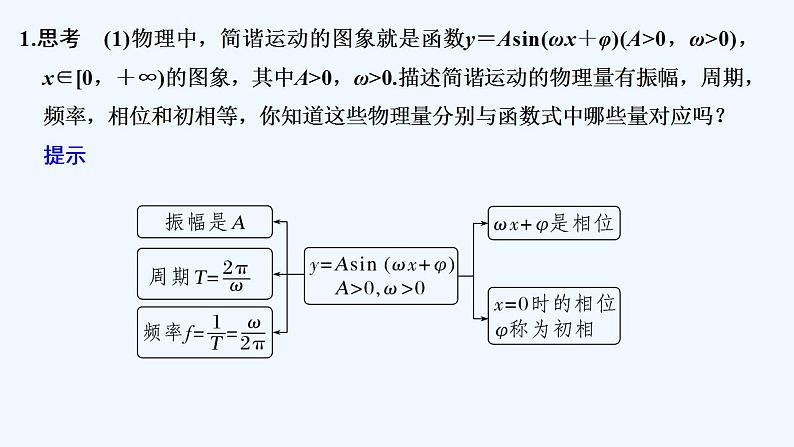
1.思考　(1)物理中，简谐运动的图象就是函数y＝Asin(ωx＋φ)(A>0，ω>0)，x∈[0，＋∞)的图象，其中A>0，ω>0.描述简谐运动的物理量有振幅，周期，频率，相位和初相等，你知道这些物理量分别与函数式中哪些量对应吗？ 提示　
(2)y＝Asin(ωx＋φ) 的解析式中字母值的确定：根据函数y＝Asin(ωx＋φ)(A>0，ω>0)的部分图象如何求A?提示　①根据图象的最高点(或最低点)确定A.
②根据函数y＝Asin(ωx＋φ)(A>0，ω>0)的部分图象如何确定ω？
2.填空　简谐运动(单摆、弹簧振子等)是一种周期运动，其运动规律可以用三角函数表达为y＝Asin(ωx＋φ)，其中x表示______，y表示相对于__________的偏离； ①A表示物体运动时离开平衡位置的最大距离，称为______；
时间
平衡位置
振幅
温馨提醒　解三角函数应用问题的基本步骤
3.做一做　(1)思考辨析，判断正误①函数y＝Asin(ωx＋φ)，x∈R的最大值为A.(　　)提示　当A>0时，ymax＝A；当A<0时，ymax＝－A.②函数y＝Asin(ωx－φ)的初相为φ.(　　)提示　初相为－φ.
×
×
√
A
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
题型一　三角函数模型在物理中的应用
列表：
描点画图：
②小球摆动时离开平衡位置的最大距离是6 厘米.③小球来回摆动一次需要1 秒(即周期).
∴ω≥300π>942，又ω∈N*，故所求最小正整数ω＝943.
题型二　三角函数模型在生活中的应用
例2 如图，游乐场中的摩天轮匀速旋转，每转一圈需要12分钟，其中心O距离地面40.5米，半径40米.如果你从最低处登上摩天轮，那么你与地面的距离将随时间的变化而变化，以你登上摩天轮的时刻开始计时.请解答下列问题.
(1)求出你与地面的距离y与时间t之间的函数解析式；
解　可以用余弦型函数来表示该函数解析式，由已知可设y＝40.5－40cos ωt(t≥0)，由周期为12分钟可知，当t＝6分钟时到达最高点，即函数取得最大值，故80.5＝40.5－40cos 6ω，
(2)当你第四次距离地面60.5米时，用了多长时间？
解得t＝4＋12k，k∈N或t＝8＋12k，k∈N，又∵t≥0，故第四次距离地面60.5米时，用了12＋8＝20(分钟).
(3)当你登上摩天轮2分钟后，你的朋友也在摩天轮最低处登上摩天轮，问：你的朋友登上摩天轮多长时间后，你和你的朋友与地面的距离之差最大？并求出最大值.
解　与地面的距离之差最大，此时你必须在你的朋友的正上方，或你的朋友在你的正上方，由周期性知，再过2分钟后，你恰好在你的朋友的正上方；再过半个周期时，恰相反，故过(6k＋2)(k∈N)分钟后，你和你的朋友与地面的距离之差最大，最大值为40米.
解决三角函数的实际应用问题必须按照一般应用题的解题步骤执行：(1)认真审题，理清问题中的已知条件与所求结论.(2)建立三角函数模型，将实际问题数学化.(3)利用三角函数的有关知识解决关于三角函数的问题，求得数学模型的解.(4)根据实际问题的意义，得出实际问题的解.(5)将所得结论返回、转译成实际问题的答案.
(2)若有一种细菌在15 ℃到25 ℃之间可以生存，那么在这段时间内，该细菌能生存多长时间？
课堂小结
1.掌握2个应用(1)三角函数在物理中的应用.(2)三角函数在生活中的应用.2.掌握4个步骤(1)收集数据，观察数据，发现是否具有周期性的重复现象.(2)制作散点图，选择函数模型进行拟合.(3)利用三角函数模型解决实际问题.(4)根据问题的实际意义，对答案的合理性进行检验.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
A.5 B.6 C.8 D.10
C
C
A
C
5.(多选)如图是某市夏季某一天的温度变化曲线，若该曲线近似地满足函数y＝Asin(ωx＋φ)＋B(A＞0，ω＞0，0<φ<π)，则下列说法正确的是(　　)
A
解析　由图象知A＋B＝30，－A＋B＝10，∴A＝10，B＝20.
∴B正确，C错误；当x＝12时，
7.如图表示相对于平均海平面的某海湾的水面高度h(米)在某天0～24时的变化情况，则水面高度h关于时间t的函数关系式为_______________________.
解析　设h＝Asin(ωt＋φ)(A＞0，ω＞0)，由图象知A＝6，T＝12，
20.5
于是f(t)在[0，24]上的最大值为12，最小值为8.故实验室这一天的最高温度为12 ℃，最低温度为8 ℃，最大温差为4 ℃.
(2)若要求实验室温度不高于11 ℃，则在哪段时间实验室需要降温？
解　依题意，当f(t)>11时，实验室需要降温，
即1010.某港口的水深y(米)是时间t(0≤t≤24，单位：小时)的函数，下面是每天不同时间与水深的关系表：
解　由表中数据可以得到水深最大值为13，最小值为7，
(2)若船舶航行时，水深至少要11.5米才是安全的，那么船舶在一天中的哪几个时间段可以安全地进出该港？
解　要想船舶安全，必须深度f(t)≥11.5，
解得12k＋1≤t≤12k＋5，k∈N，又0≤t≤24，当k＝0时，1≤t≤5；当k＝1时，13≤t≤17；故船舶安全进港的时间段为1：00～5：00，13：00～17：00.
A
二、能力提升
13.为迎接夏季旅游旺季的到来，少林寺单独设置了一个专门安排旅客住宿的客栈，寺庙的工作人员发现为游客准备的食物有些月份剩余不少，浪费很严重，为了控制经营成本，减少浪费，就想适时调整投入.为此他们统计每个月入住的游客人数，发现每年各个月份来客栈入住的游客人数会发生周期性的变化，并且有以下规律： ①每年相同的月份，入住客栈的游客人数基本相同； ②入住客栈的游客人数在2月份最少，在8月份最多，相差约400人； ③2月份入住客栈的游客约为100人，随后逐月递增直到8月份达到最多. (1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系； (2)请问哪几个月份要准备400份以上的食物？
解得12k＋6≤x≤12k＋10，k∈Z.因为x∈N*，且1≤x≤12，所以x＝6，7，8，9，10.故只有6，7，8，9，10这五个月份要准备400份以上的食物.
14.如图，摩天轮的半径为50 m，圆心O距地面的高度为65 m.已知摩天轮按逆时针方向匀速转动，每30 min转动一圈.游客在摩天轮的舱位转到距离地面最近的位置进舱.
三、创新拓展
(1)游客进入摩天轮的舱位，开始转动t min后，他距离地面的高度为h，求h关于t的函数解析式；
解　如图以摩天轮的圆心为坐标原点，水平方向为x轴，建立平面直角坐标系.设游客的位置为点P.
(2)已知在距离地面超过40 m的高度，游客可以观看到游乐场全景，那么在摩天轮转动一圈的过程中，游客可以观看到游乐场全景的时间是多少？