2021-2022学年河北省保定市名校高二（下）第二次联考数学试卷（B1）（Word解析版）

2021-2022学年河北省保定市名校高二（下）第二次联考数学试卷（B1）

一、单选题（本大题共8小题，共40分）

1. (    )

A.  B.  C.  D.

2. 已知随机变量满足，则(    )

A. 或 B.  C.  D.

3. 的展开式中各项系数之和为，各二项式系数之和为，则(    )

A.  B.  C.  D.

4. 某校有东、南、西、北四个校门，为了加大防疫的力度，学校做出如下规定：北门封闭，学生只能从东门或西门进入校园，教师不能从西门进入校园．现有名教师和名学生要进入校园不分先后顺序，则这人进入校园的方式共有(    )

A. 种 B. 种 C. 种 D. 种

5. 的展开式中的系数为(    )

A.  B.  C.  D.

6. 已知，则(    )

A.  B.  C.  D.

7. 中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱．假设中国空间站要安排名航天员开展实验，其中每个舱安排人．若甲．乙两人不被安排在同一个舱内做实验，则不同的安排方案共有(    )

A. 种 B. 种 C. 种 D. 种

8. 某实验测试的规则如下：每位学生最多可做次实验，一旦实验成功，则停止实验，否则做完次为止．设某学生每次实验成功的概率为，实验次数为随机变量，若的数学期望，则的取值范围是(    )

A.  B.  C.  D.

二、多选题（本大题共4小题，共20分）

9. 已知随机变量的分布列如下表：

若，则(    )

A.  B.  C.  D.

10. 已知，则(    )

A.
B.
C.
D.

11. 有台车床加工同一型号的零件，第台车床加工的次品率为，第台车床加工的次品率为，第台车床加工的次品率为，加工出来的零件混放在一起．已知第，，台车床加工的零件数分别占总数的，，，现从中任意选取个零件，则(    )

A. 该零件是由第台车床加工的次品的概率为
B. 该零件是次品的概率为
C. 在取到的零件是次品的前提下，该零件是由第台车床加工的概率为
D. 在取到的零件是次品的前提下，该零件是由第台车床加工的概率为

12. 甲、乙两人拿两颗质地均匀的骰子做抛掷游戏．规则如下：由一人同时掷两颗骰子，观察两颗骰子向上的点数之和，若两颗骰子的点数之和为两位数，则由原掷骰子的人继续掷；若掷出的点数之和不是两位数，就由对方接着掷．第一次由甲开始掷，设第次由甲掷的概率为，则(    )

A.  B.
C.  D.

三、填空题（本大题共4小题，共20分）

13. 展开式中的常数项为______．
14. 哥德巴赫猜想是指“每个大于的偶数都可以表示为两个素数的和”，例如，，在不超过的素数中，随机选取两个数，其和等于的概率为______．
15. 已知随机变量，，则的最小值为______，此时，______．
16. 将人分成组，每组至少人，则不同的分组方法种数为______．

四、解答题（本大题共6小题，共70分）

17. 已知为正整数展开式的中间项是第项．
    求的值；
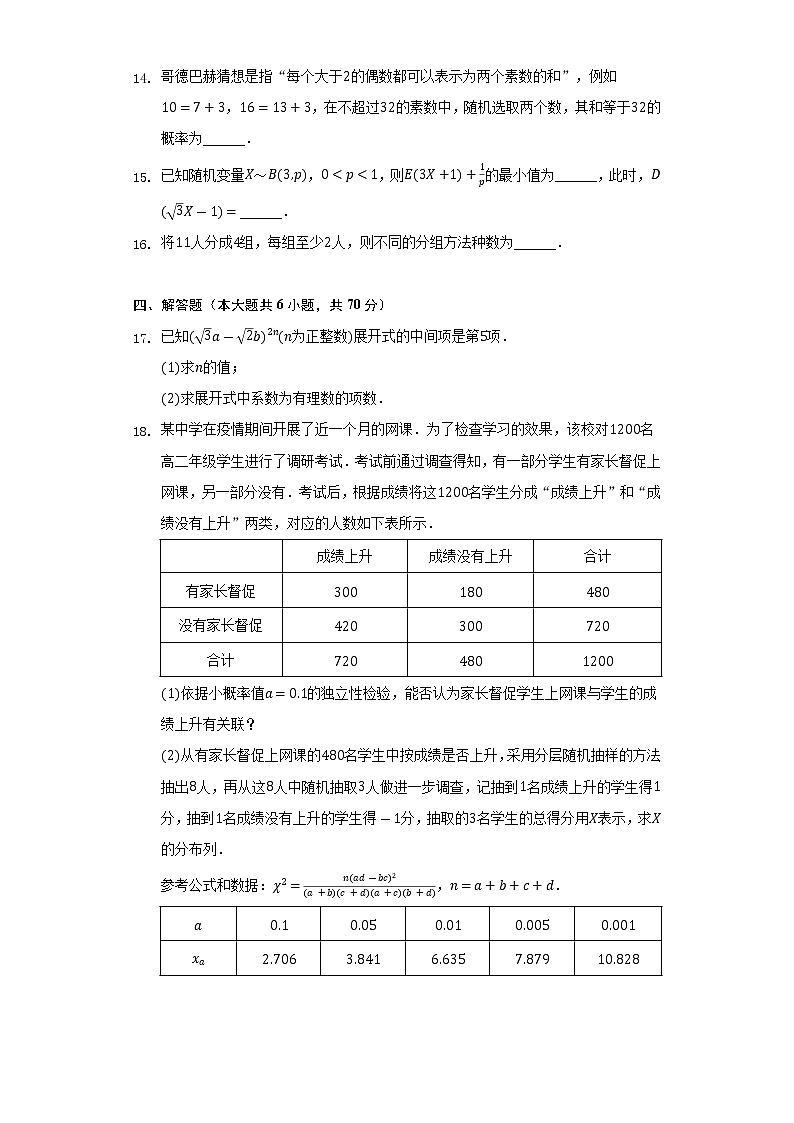
    求展开式中系数为有理数的项数．
18. 某中学在疫情期间开展了近一个月的网课．为了检查学习的效果，该校对名高二年级学生进行了调研考试．考试前通过调查得知，有一部分学生有家长督促上网课，另一部分没有．考试后，根据成绩将这名学生分成“成绩上升”和“成绩没有上升”两类，对应的人数如下表所示．

依据小概率值的独立性检验，能否认为家长督促学生上网课与学生的成绩上升有关联？
从有家长督促上网课的名学生中按成绩是否上升，采用分层随机抽样的方法抽出人，再从这人中随机抽取人做进一步调查，记抽到名成绩上升的学生得分，抽到名成绩没有上升的学生得分，抽取的名学生的总得分用表示，求的分布列．
参考公式和数据：，．

19. 将名女生和名男生排成一行．
    若要求名女生相邻，则有多少种不同的排法？
    若要求男生甲站在正中间，且名女生各不相邻，则有多少种不同的排法？
20. 现有关于与的组数据，如下表所示．

依据表中的统计数据，判断与是否具有较高的线性相关程度；若，则，线性相关程度一般，若，则线性相关程度较高，计算时精确度为
求关于的经验回归方程，请预测当时的值．
参考数据：．
附：样本相关系数，，

21. 某食品厂生产一种零食，该种零食每袋的质量单位：服从正态分布．
    当质检员随机抽检袋该种零食时，测得袋零食的质量为，他立即要求停止生产，检查设备，请你根据所学知识，判断该质检员的决定是否有道理，并说明判断的依据．
    规定：这种零食的质量在的为合格品．
    求这种零食的合格率；结果精确到
    从该种零食中任意挑选袋，合格品的袋数为，若的数学期望大于，求的最小值．
    参考数据：若，则，，．
22. 为弘扬奥运精神，某校开展了“冬奥”相关知识趣味竞赛活动．现有甲，乙两名同学进行比赛，共有两道题目，一次回答一道题目．规则如下：
    抛一次质地均匀的硬币，若正面向上，则由甲回答一个问题，若反面向上，则由乙回答一个问题．
    回答正确者得分，另一人得分；回答错误者得分，另一人得分．
    若两道题目全部回答完，则比赛结束，计算两人的最终得分．
    已知甲答对每道题目的概率为，乙答对每道题目的概率为，且两人每道题目是否回答正确相互独立．
    求乙同学最终得分的概率；
    记为甲同学的最终得分，求的分布列和数学期望．
    

答案和解析

1.【答案】 

【解析】解：由组合数公式可得，．
故选：．
运用组合数公式，即可求解．
本题主要考组合数公式，属于基础题．
 

2.【答案】 

【解析】解：随机变量满足，
，解得或舍去．
故选：．
依题意，，解出即可．
本题考查离散型随机变量期望的求解，考查运算求解能力，属于基础题．
 

3.【答案】 

【解析】解：令，得展开式中各项系数之和，
因为二项式系数之和，所以．
故选：．
令可得，由二项式系数的性质可得，计算可得结论．
本题主要考查二项式定理，二项式系数的性质及赋值法的应用，考查运算求解能力，属于基础题．
 

4.【答案】 

【解析】解：因为北门封闭，学生只能从东门或西门进入校园，所以，名学生进入校园的方式共有种，
又教师不能从西门进入校园，所以教师只能从东门或南门进入校园，所以，名教师进入校园的方式共有种．
所以，由分步乘法计数原理可得，这人进入校园的方式共有种．
故选：．
根据题意，先分析名学生进入校园的方式，在分析名教师进入校园的方式，最后利用分步乘法计数原理计算即可．
本题考查了分步乘法计数原理，属于基础题．
 

5.【答案】 

【解析】解：因为的展开式中的系数为，
所以的展开式中的系数为，
故选：．
根据二项式定理展开式，即可直接解出．
本题考查了二项式定理的展开式，学生的数学运算能力，属于基础题．
 

6.【答案】 

【解析】解：，
，
．
故选：．
先求出，再求解即可．
本题考查离散型随机变量的期望与方差，考查运算求解能力，属于基础题．
 

7.【答案】 

【解析】解：将名航天员每个舱安排人开展实验的所有安排方法数为，其中甲，乙两人被安排在同一个能内做实验的安排方法数为，
所以满足条件的不同的安排方案数为．
故选：．
先求出每个舱安排人的所有方法，再求出其中甲乙两人被安排到同一舱内做实验的安排方法，两者相减可得满足条件的安排方案数．
本题考查了排列组合及对立事件，属于基础题．
 

8.【答案】 

【解析】解：依题意，，
又，故，
解该不等式可得或，
又，
．
故选：．
先求出，可得，由此可得的取值范围．
本题考查离散型随机变量的期望，考查运算求解能力，属于基础题．
 

9.【答案】 

【解析】解：由题可知，，记为
若，则，记为，
联立，解得，．
故选：．
根据题意得到，，联立求解即可．
本题考查离散型概率分布列的概率的求法，解题时要认真审题，是基础题．
 

10.【答案】 

【解析】解：对于选项A，令，得，则，即选项A正确；
对于选项B，令，得，所以，即选项B正确；
对于选项C，由二项式展开式通项公式可得：，即选项C错误；
对于选项D，令，得，所以，即选项D正确，
故选：．
由二项式定理的应用，结合二项式展开式系数的求法求解即可．
本题考查了二项式定理的应用，重点考查了二项式展开式系数的求法，属基础题．
 

11.【答案】 

【解析】解：有台车床加工同一型号的零件，第台车床加工的次品率为，第台车床加工的次品率为，
第台车床加工的次品率为，加工出来的零件混放在一起．
第，，台车床加工的零件数分别占总数的，，，
对于，记事件为“零件由第台车床加工”，记事件为“零件为次品”，
则，，，，
，．
由条件概率得该零件是由第台车床加工的次品的概率：
，故A错误；
对于，由全概率公式得该零件是次品的概率为：
，故B正确；
对于，在取到的零件是次品的前提下，由贝叶斯公式得该零件是由第台车床加工的概率为：
，故C正确；
对于，在取到的零件是次品的前提下，由贝叶斯公式得该零件是由第台车床加工的概率为：
，故D正确．
故选：．
利用条件概率判断；利用全概率公式判断；利用贝叶斯公式判断．
本题考查概率的运算，考查条件概率、全概率公式、贝叶斯公式等基础知识，考查运算求解能力，是基础题．
 

12.【答案】 

【解析】解：两颗骰子的点数之和为两位数的概率为．
第次由甲掷有两种情况：
第次由甲掷，第次由甲掷，概率为；
第次由乙掷，第次由甲掷，概率为．
这两种情况是对立的，所以当时，，即，
所以，
则数列是以为首项，为公比的等比数列，
所以，所以，，．
故选：．
据题意列出第次由甲掷的两种情况，根据对立事件加法公式求得递推关系式，转化为构造数列求解通项公式的问题即可得到答案．
本题考查古典概型的问题，构造等比数列是解决本题的关键．
 

13.【答案】 

【解析】解：展开式中的通项，
当时，常数项为，
故答案为：．
根据二项式定理的展开式的通项公式，即可解出．
本题考查了二项式定理，学生的数学运算能力，属于基础题．
 

14.【答案】 

【解析】解：不超过的素数有，，，，，，，，，，共个，
在不超过的素数中，随机选取两个数，基本事件总数为个，
满足和为的组合是，共两个，
故其和等于的概率为．
故答案为：．
根据素数的定义及组合数的定义，结合古典概型的计算公式即可求解．
本题主要考查古典概型的问题，熟记概率的计算公式即可，属于常考题型．
 

15.【答案】   

【解析】解：由题意可知，，所以，，
所以，
所以，
当且仅当，即时，等号成立，所以的最小值为，
此时，
所以．
故答案为：；．
根据二项分布的期望与方差公式，再利用基本不等式求最值，结合二项分布的期望与方差的性质即可求解．
本题主要考查均值的计算，方差的计算等知识，属于基础题．
 

16.【答案】 

【解析】解：依题意，可得各组的人数为，，，或，，，或，，，，
故不同的分组方法种数为．
故答案为：．
依题意，可得各组的人数为，，，或，，，或，，，，根据分类计数原理可得．
本题考查了不均匀分组，考查了运算能力，属于基础题．
 

17.【答案】解：因为正偶数，所以展开式的中间项为第项，
所以，解得；
由知，
其通项为，
若系数为有理数，则，均为整数，则，，，，，
所以展开式中系数为有理数的项数为． 

【解析】根据二项式定理的展开式，即可解出；
根据二项式定理的展开式的通项公式，即可解出．
本题考查了二项式定理，学生的数学运算能力，属于基础题．
 

18.【答案】解：零假设：家长督促学生上课与学生的成绩上升无关联，
由题中数据可知，，
依据小概率值的独立性检验，我们推断成立，
所以，可以认为家长督促学生上网课与学生的成绩上升无关联；
由题意可知，从有家长督促的名学生中按分层随机抽样法抽出人，其中成绩上升的有人，成绩没有上升的有人，
记抽到名成绩上升的学生得分，抽到名成绩没有上升的学生得分，抽取的名学生的总得分用表示，
则的所有可能取值为，，，，对应概率分别为：，，，，
所以，的分布列为：

【解析】根据联表数据计算，与临界值比较得出结论；
结合分层抽样所得数据，写出的所有可能，计算对应的概率，得出分布列即可．
本题考查离散型概率分布列及独立性检验，解题时要认真审题，是中档题．
 

19.【答案】解：若要求名女生相邻，则有种不同的排法；
要求男生甲站在正中间，且名女生各不相邻，则有种不同的排法． 

【解析】由排列、组合及简单计数问题，结合相邻问题求解即可；
由排列、组合及简单计数问题，结合不相邻问题求解即可．
本题考查了排列、组合及简单计数问题，重点考查了相邻问题及不相邻问题，属基础题．
 

20.【答案】解：由表中数据可得，，
，，，
由相关系数的公式可得，，
，
与具有较高的线性相关程度．
，，
，
，，
则，
故线性回归方程为，
令，则，
故预测当时，的值为． 

【解析】根据已知条件，结合相关系数的求解，即可求解．
结合最小二乘法求出线性回归方程，再将代入上式，即可求解．
本题主要考查最小二乘法求解线性回归方程，以及相关系数的求解，属于基础题．
 

21.【答案】解：该种零食每袋的质量单位：服从正态分布，
可得，，
则，，
所以，
所以远小于，此事件为小概率事件，
所以该质检员的决定有道理．
因为，，所以，，
由题意可知当零食质量满足时为合格品，
所以这种零食的合格率为．
由题意可知，
则，
则．
故的最小值为． 

【解析】由正态分布的特点和小概率事件，可得结论；
结合，，可得结论；
，由二项分布的期望，解不等式可得所求值．
本题考查概率的正态分布、二项分布，考查运算能力，属于基础题．
 

22.【答案】解：记乙同学最终得分为事件，
则可能情况为甲回答两题且错两题；甲、乙各答一题且各对一题；乙回答两题且对一题错一题，
则，
所以乙同学得分的概率是．
甲同学的最终得分的所有可能取值是，，，，．
当时，其概率值为：
，
当时，其概率值为：
，
当时，其概率值为：
，
当时，其概率值为：
，
当时，其概率值为：
．
的分布列为：

结合分布列可计算随机变量的数学期望：
，
所以的数学期望为． 

【解析】根据题意得到乙同学最终得分的所有可能情况，求出其概率再相加即可；
根据题意写出甲同学的最终得分的所有可能取值，求出其概率再运用期望计算公式求得的数学期望即可．
本题主要考查离散型随机变量及其分布列，概率统计的实际应用等知识，属于中等题．