2021-2022学年山西省朔州市怀仁市七年级（下）期末数学试卷（Word解析版）

绝密★启用前

2021-2022学年山西省朔州市怀仁市七年级（下）期末数学试卷

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 若，则的值为(    )

A.  B.  C.  D.

2. 下面调查方式中，合适的是(    )

A. 试航前对我国第一艘国产航母各系统的检查，选择抽样调查方式
B. 了解一批袋装食品是否含有防腐剂，选择普查方式
C. 为有效控制“新冠疫情”的传播，对国外入境人员的健康状况，采用普查方式
D. 调查某新型防火材料的防火性能，采用普查的方式

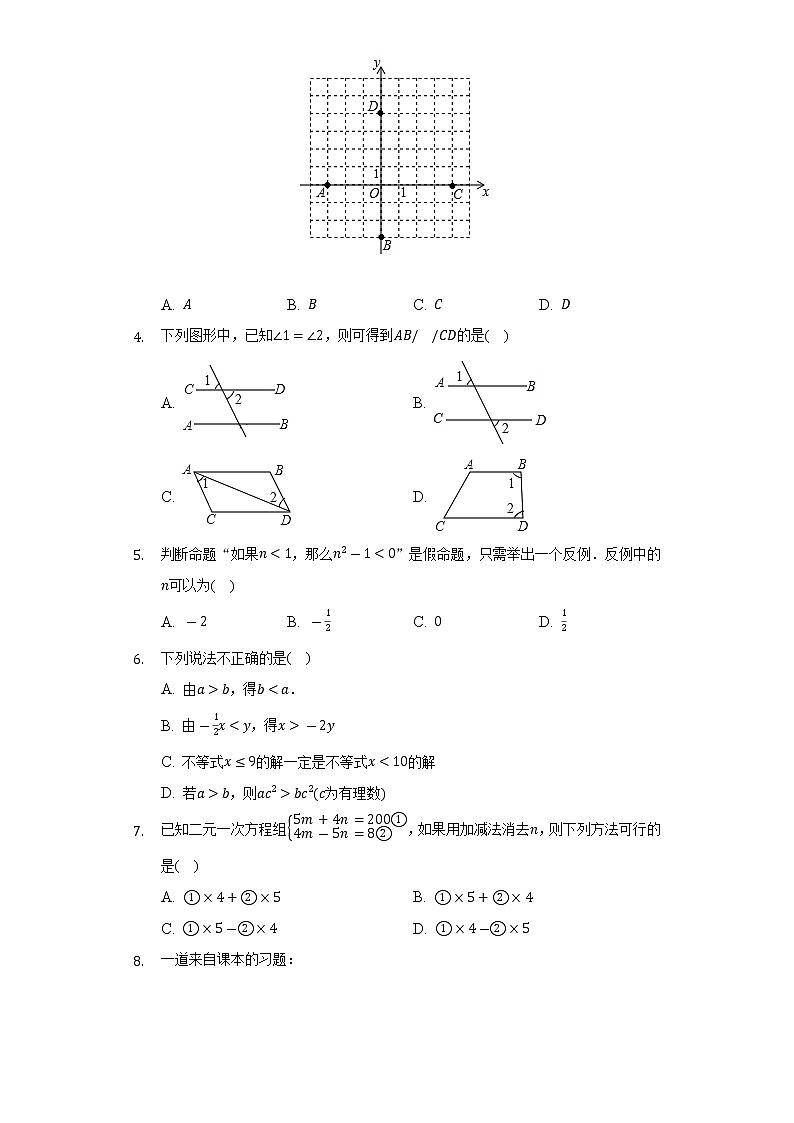
3. 如图，坐标平面上有原点与、、、四点．若有一直线通过点且与轴垂直，则也会通过下列哪一点？(    )

A.  B.  C.  D.

4. 下列图形中，已知，则可得到的是(    )

A.  B.
C.  D.

5. 判断命题“如果，那么”是假命题，只需举出一个反例．反例中的可以为(    )

A.  B.  C.  D.

6. 下列说法不正确的是(    )

A. 由，得．
B. 由，得
C. 不等式的解一定是不等式的解
D. 若，则为有理数

7. 已知二元一次方程组，如果用加减法消去，则下列方法可行的是(    )

A.  B.
C.  D.

8. 一道来自课本的习题：

小红将这个实际问题转化为二元一次方程组问题，采用间接设法：
设坡路有，平路有，则全程为已经列出一个方程，则另一个方程正确的是(    )

A.  B.  C.  D.

9. 为节约用电，某市根据每户居民每月用电量分为三档频数户收费．第一档电价：每月用电量低于度，每度元；第二档电价：每月用电量为度，每度元；第三档电价：每月用电量超过度，每度元小明同学对该市有居民的某小区月用电量单位：度进行了抽样调查，绘制了如图所示的统计图．下列说法不合理的是(    )

A. 本次抽样调查的样本容量为
B. 估计该小区按第一档电价交费的居民户数最多
C. 该小区按第二档电价交费的居民有户
D. 该小区按第三档电价交费的居民比例约为

10. 已知方程组的解满足，则取值范围是(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共5小题，共15.0分）

11. 在实数，，，中，最小的数是______．
12. 如图，把长方形沿对折，若，则的度数等于______ ．

13. 在一次体育测试中，名女生完成仰卧起坐的个数如下：、、、、、、、、、，则名女生仰卧起坐个数不少于个的频率为______．
14. 已知是关于，的二元一次方程，则______．
15. 在“新冠肺炎”这场没有硝烟的战争中，各行各业都涌现出了一批“最美逆行者”，其中抗疫最前沿的就是护士．某医院安排护士若干名负责护理新冠病人，每名护士护理名新冠病人，有名新冠病人没人护理，如果每名护士护理名新冠病人，有一名护士护理的新冠病人多于人不足人，这个医院安排了______名护士护理新冠病人．

三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）

16. 本小题分
    计算：；
    解方程：．
17. 本小题分
    解方程组：
    ；
    ．
18. 本小题分
    解不等式组：
    ，把解集在数轴上表示出来；
    ，求出它的所有整数解的和．
19. 本小题分
    如图，点、、、在一条直线上，与交于点，，，求证：．

20. 本小题分
    如图，在网格中，每个小正方形的边长均为个单位长度．我们将小正方形的顶点叫做格点，的三个顶点均在格点上．
    
    将先向右平移个单位长度，再向上平移个单位长度，得到，画出平移后的；
    建立适当的平面直角坐标系，使得点的坐为；
    在的条件下，直接写出点的坐标．
21. 本小题分
    为了庆祝学校体育运动会，某校组织七年级学生进行“艺术体操表演”为了达到整齐划一的效果，需了解学生的身高，现随机抽取该校七年级学生进行抽样调查，根据所得数据绘制出如图计图表：

根据图表提供的信息，回答下列问题：
这次抽样调查，一共抽取学生______人；
扇形统计图中，扇形的圆心角度数是______；
请补全频率分布直方图；
已知该校七年级共有学生人，请估计身高在的学生约有多少人？

22. 本小题分
    某中学开学初到商场购买、两种品牌的足球，购买种品牌的足球个，种品牌的足球个，共花费元．已知购买一个种品牌的足球比购买一个种品牌的足球多花元
    求购买一个种品牌、一个种品牌的足球各需多少元？
    学校为了响应习总书记“足球进校园”的号召，决定再次购进、两种品牌足球共个，正好赶上商场对商品价格进行调整，品牌足球售价比第一次购买时提高元，品牌足球按第一次购买时售价的折出售，如果学校此次购买、两种品牌足球的总费用不超过第一次花费的，且保证这次购买的种品牌足球不少于个，则这次学校有哪几种购买方案？
23. 本小题分
    如图，已知，，．
    
    若，请直接写出的度数；
    探索与之间满足的数量关系，并说明理由；
    如图，平分，平分，的反向延长线交于点，求的度数．
    

答案和解析

1.【答案】 

【解析】解：，
．
故选：．
根据算术平方根的定义解决此题．
本题主要考查算术平方根，熟练掌握算术平方根的定义是解决本题的关键．
 

2.【答案】 

【解析】解：、试航前对我国第一艘国产航母各系统的检查，零部件很重要，应全面检查；
B、了解一批袋装食品是否含有防腐剂，适合抽样调查；
C、为有效控制“新冠疫情”的传播，对国外入境人员的健康状况，适合采用普查方式；
D、调査某新型防火材料的防火性能，适合抽样调查．
故选：．
由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
 

3.【答案】 

【解析】解：如图所示：

有一直线通过点且与轴垂直，则也会通过点．
故选：．
直接利用点的坐标，正确结合坐标系分析即可．
此题主要考查了点的坐标，正确结合平面直角坐标系分析是解题的关键．
 

4.【答案】 

【解析】【解析】
此题主要考查了平行线的判定，关键是掌握平行线的判定定理．先确定两角之间的位置关系，再根据平行线的判定来确定是否平行，以及哪两条直线平行．
【解答】
解：和是对顶角，不能判断，此选项不正确；
B.和的对顶角是同位角，且相等，所以，此选项正确；
C.和是内错角，且相等，故AC，不是，此选项错误；
D.和互为同旁内角，同旁内角相等，两直线不一定平行，此选项错误．
故选：．
 

5.【答案】 

【解析】解：当时，满足，但，
所以判断命题“如果，那么”是假命题，举出．
故选：．
反例中的满足，使，从而对各选项进行判断．
本题考查了命题与定理：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
 

6.【答案】 

【解析】解：，
，
故A不符合题意；
，
由不等式的基本性质，，
故B不符合题意；
，则必有，
故C不符合题意；
，时，
，
是有理数，
当时，，
故D符合题意；
故选：．
由不等式的基本性质解题即可．
本题考查一元一次不等式的性质，熟练掌握一元一次不等式的性质是解题的关键．
 

7.【答案】 

【解析】解：，
得，，
得，，
得，，
故选：．
根据加减消元法解二元一次方程组的方法求解即可．
本题考查解二元一次方程组，熟练掌握加减消元法解二元一次方程组的方法是解题的关键．
 

8.【答案】 

【解析】解：依题意有：另一个方程正确的是．
故选：．
根据时间路程速度结合从乙地到甲地需分钟，即可得出关于，的二元一次方程组，即可得出结论．
本题考查了由实际问题抽象出二元一次方程，找准等量关系，正确列出二元一次方程组是解题的关键．
 

9.【答案】 

【解析】解：本次抽样调查的样本容量户，故A不符合题意．
估计该小区按第一档电价交费的居民户数占，第二档占，第三档占，故B，不符合题意．
该小区按第二档电价交费的居民约为户，故C符合题意，
故选：．
利用直方图中的信息一一判断即可．
本题考查频数分布直方图，样本估计总体的思想等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

10.【答案】 

【解析】解：将两个方程相加可得，
，
，
，
解得，
故选：．
将两个方程相加整理得出，再根据题意列出关于的不等式，解之可得．
本题主要考查解一元一次不等式，解题的关键是根据题意列出关于的不等式，并熟练掌握解不等式的步骤和依据．
 

11.【答案】 

【解析】解：根据实数比较大小的方法，可得，
故在实数，，，中，最小的数是．
故答案为：．
正实数都大于，负实数都小于，正实数大于一切负实数，两个负实数绝对值大的反而小，据此即可求解．
此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数负实数，两个负实数绝对值大的反而小．
 

12.【答案】 

【解析】

【分析】
此题考查了折叠的性质和平行线的性质．根据折叠的性质，得，再根据平行线的性质即可求得的度数．
【解答】
解：根据长方形沿对折，，得
．
，
．
故答案为．  

13.【答案】 

【解析】解：仰卧起坐个数不少于个的有、、、、、共个，
所以，频率．
故答案为：．
用仰卧起坐个数不少于个的频数除以女生总人数计算即可得解．
本题考查了频数与频率，频率．
 

14.【答案】 

【解析】解：是关于，的二元一次方程，
，，
解得：，，
故．
故答案为：．
由二元一次方程的定义解答即可．
本题主要考查二元一次方程的定义，掌握二元一次方程的未知项的次数为是解题的关键．
 

15.【答案】 

【解析】解：设医院安排了名护士，由题意得，
，
解得，，
为整数，
．
故答案为：．
设医院安排了名护士，由题意列出不等式组，则可得出答案．
本题考查了一元一次不等式组的应用，根据各数量之间的关系，正确列出一元一次不等式组是解题的关键．
 

16.【答案】解：

．

，
，
解得：． 

【解析】首先计算开平方和开立方，然后从左向右依次计算，求出算式的值即可．
根据立方根的含义和求法，求出的值，进而求出的值即可．
此题主要考查了立方根的含义和求法，以及实数的运算，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．
 

17.【答案】解：，
得：，
解得：，
把代入得：，
则方程组的解为；
方程组整理得：，
得：，
解得：，
得：，
解得：，
则方程组的解为． 

【解析】方程组利用加减消元法求出解即可；
方程组整理后，利用加减消元法求出解即可．
此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
 

18.【答案】解：移项，得：，
合并同类项，得：，
系数化为，得：，
将不等式解集表示在数轴上如下：

解不等式，得：，
解不等式，得：，
则不等式组的解集为，
所以不等式整数解的和为． 

【解析】根据解一元一次不等式基本步骤：移项、合并同类项、系数化为可得；
分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集，继而得出整数解的和．
本题考查的是一元一次不等式组整数解，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
 

19.【答案】证明：，
，
，
，
，
． 

【解析】本题考查了平行线的性质与判定，根据平行线的性质可得，又，可得，利用平行线的判定与性质得，即可得出．
 

20.【答案】解：如图，为所作；

如图，
点的坐标为． 

【解析】本题考查了作图平移变换：确定平移后图形的基本要素有两个：平移方向、平移距离．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
利用网格特点和平移的性质画出、、的对应点、、，从而得到；
利用点坐标画出直角坐标系；
利用第一象限点的坐标特征写出点的坐标．
 

21.【答案】   

【解析】解：这次抽样调查，一共抽取学生人；
故答案为：．
扇形统计图中，扇形的圆心角度数是，
故答案为：；
身高在的人数为：人，
补全频数分布直方图如图所示；
人，
答：估计身高在的学生约有人．
用组人数其所占的百分数即可得到结论；
利用乘以对应的比例即可求解；
根据题意补全频数分布直方图即可；
利用总人数乘以对应的比例．
本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
 

22.【答案】解：设种品牌足球的单价为元，种品牌足球的单价为元，
依题意得：
，
解得：．
答：购买一个种品牌的足球需要元，购买一个种品牌的足球需要元．

设第二次购买种足球个，则购买种足球个，
依题意得：，
解得：．
故这次学校购买足球有三种方案：
方案一：购买种足球个，种足球个；
方案二：购买种足球个，种足球个；
方案三：购买种足球个，种足球个． 

【解析】设种品牌足球的单价为元，种品牌足球的单价为元，根据“总费用买种足球费用买种足球费用，以及种足球单价比种足球贵元”可得出关于、的二元一次方程组，解方程组即可得出结论；
设第二次购买种足球个，则购买种足球个，根据“总费用买种足球费用买种足球费用，以及种足球不小于个”可得出关于的一元一次不等式组，解不等式组可得出的取值范围，由此即可得出结论．
本题考查了二元一次方程组的应用以及一元一次不等式组的应用，解题的关键是：根据数量关系找出关于、的二元一次方程组；根据数量关系找出关于的一元一次不等式组．本题属于中档题，难度不大，解决该题型题目时，根据数量关系列出方程方程组、不等式或不等式组是关键．
 

23.【答案】解：如图，分别过点，作，，

，
，，
又，，
，
，
又，
，
，，
，
，
；
故答案为：；

如图，分别过点，作，，
，
，，
又，，
，
，
又，
，
，，
，
；

如图，过点作，

由知，，
设，则，
平分，平分，
，，
，
，，
，
． 

【解析】本题考查了平行线的性质，角平分线的定义，熟练掌握平行线的性质定理是解题的关键．
如图，分别过点，作，，根据平行线的性质得到，，由，，得到，根据平行线的性质，得到，代入数据即可得到结论；
如图，根据平行线的性质得到，，由，，得到，根据平行线的性质得到，代入计算，得到结论：；
如图，过点作，设，则，根据角平分线的定义得到，，根据平行线的性质得到，，于是得到结论．