初中数学北师大版九年级上册1 反比例函数教学ppt课件

这是一份初中数学北师大版九年级上册1 反比例函数教学ppt课件，共31页。PPT课件主要包含了学习目标，UIR，导入新课，舞台的灯光效果，合作探究，讲授新课，一般地形如，想一想，是k3，练一练等内容，欢迎下载使用。

1. 理解并掌握反比例函数的概念. (重点)2. 从实际问题中抽象出反比例函数的概念，能根据已知 条件确定反比例函数的解析式. (重点、难点)
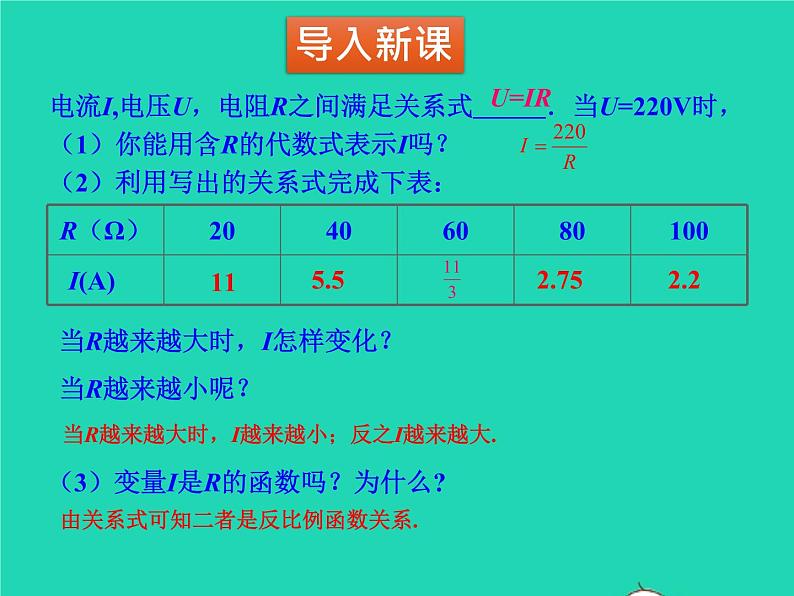
电流I,电压U，电阻R之间满足关系式 　　 ．当U=220V时，（1）你能用含R的代数式表示I吗？（2）利用写出的关系式完成下表：
当R越来越大时，I怎样变化？当R越来越小呢？
（3）变量I是R的函数吗？为什么?
当R越来越大时，I越来越小；反之I越来越大.
由关系式可知二者是反比例函数关系.
舞台灯光可以在很短的时间内将阳光灿烂的晴日变成浓云密布的阴天,或由黑夜变成白昼,这样的效果就是通过改变电阻来控制电流的变化实现的.因为当电流I较小时,灯光较暗;反之,当电流I较大时,灯光较亮.
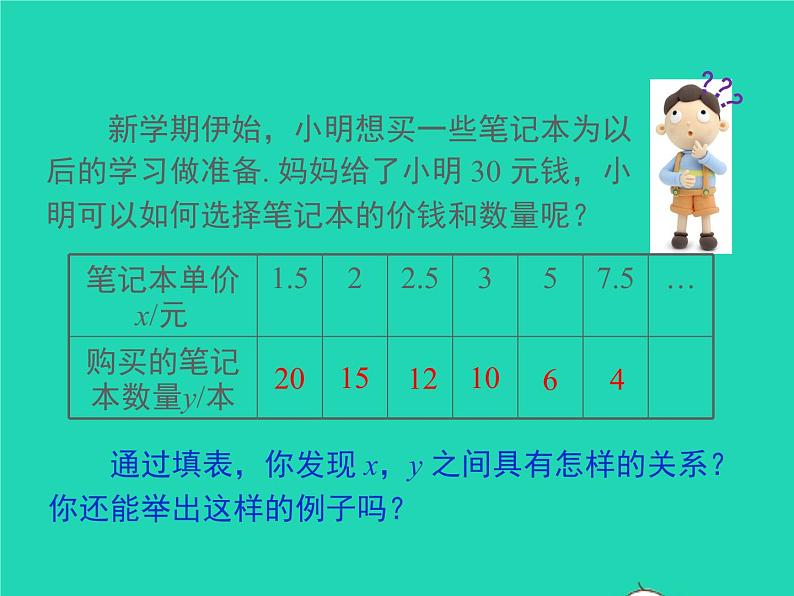
新学期伊始，小明想买一些笔记本为以后的学习做准备. 妈妈给了小明 30 元钱，小明可以如何选择笔记本的价钱和数量呢？
通过填表，你发现 x，y 之间具有怎样的关系？你还能举出这样的例子吗？
下列问题中，变量间具有函数关系吗？如果有，请写出它们的解析式.
(1)京沪高速鉄路全长约为1 318 km,列车沿京沪高速公路从上海驶往北京,列车行驶的平均速度v(km/h)随行完全程所需的时间t(h) 的变化而变化.
(2) 某住宅小区要种植一块面积为 1000 m2 的矩形草 坪，草坪的长 y (单位：m) 随宽 x (单位：m)的 变化而变化；
(3) 已知北京市的总面积为1.68×104 km2 ，人均占 有面积 S (km2/人) 随全市总人口 n (单位：人) 的 变化而变化.
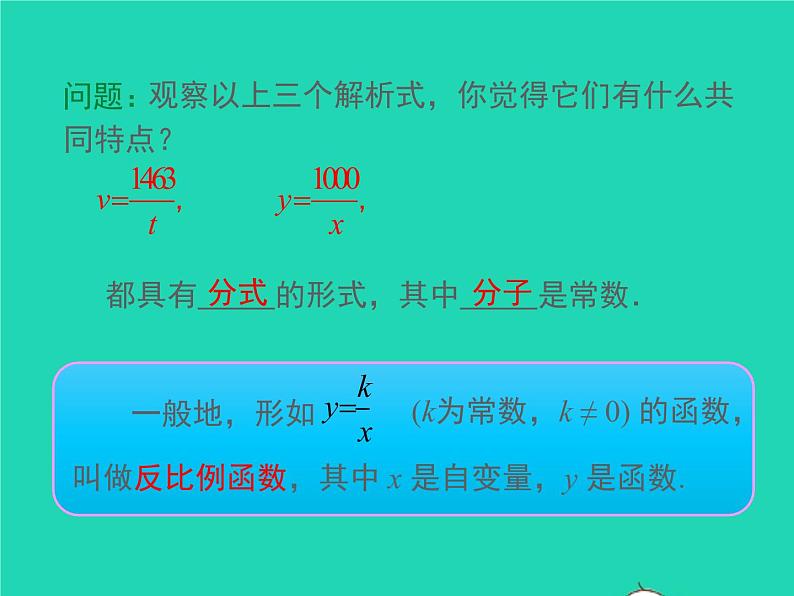
观察以上三个解析式，你觉得它们有什么共同特点？
都具有 的形式，其中 是常数．
(k为常数，k ≠ 0) 的函数，叫做反比例函数，其中 x 是自变量，y 是函数.
因为 x 作为分母，不能等于零，因此自变量 x 的取值范围是所有非零实数.
但实际问题中，应根据具体情况来确定反比例函数自变量的取值范围.
反比例函数的三种表达方式：(注意 k ≠ 0)
下列函数是不是反比例函数？若是，请指出 k 的值.
解得 k =－2.
方法总结：已知某个函数为反比例函数，只需要根据反比例函数的定义列出方程(组)求解即可.
1. 已知函数 是反比例函数，则 k 必须满足 .
2. 当m= 时， 是反比例函数.
例2 已知 y 是 x 的反比例函数，并且当 x=2时，y=6.(1) 写出 y 关于 x 的函数解析式；
解得 k =12.
(2) 当 x=4 时，求 y 的值.
方法总结：用待定系数法求反比例函数解析式的一般步骤：①设出含有待定系数的反比例函数解析式，②将已知条件(自变量与函数的对应值)代入解析式，得到关于待定系数的方程；③解方程，求出待定系数； ④写出反比例函数解析式.
已知变量 y 与 x 成反比例，且当 x=3时，y=－4.(1) 写出 y 关于 x 的函数解析式；(2) 当 y=6 时，求 x 的值.
解得 k =－12.
解得 x =－2.
例3 人的视觉机能受运动速度的影响很大，行驶中司机在驾驶室内观察前方物体是动态的，车速增加，视野变窄. 当车速为 50km/h 时，视野为 80 度，如果视野 f (度) 是车速 v (km/h) 的反比例函数，求 f 关于 v 的函数解析式，并计算当车速为100km/h 时视野的度数.
当 v=100 时，f =40.所以当车速为100km/h 时视野为40度.
解得 k =4000.
如图所示，已知菱形 ABCD 的面积为180，设它的两条对角线 AC，BD的长分别为x，y. 写出变量 y与 x 之间的关系式，并指出它是什么函数.
解:因为菱形的面积等于两条对角线长乘积的一半，
1. 生活中有许多反比例函数的例子，在下面的实例中， x 和 y 成反比例函数关系的有 ( )
① x人共饮水10 kg，平均每人饮水 y kg；②底面半径为 x m，高为 y m的圆柱形水桶的体积为10 m3；③用铁丝做一个圆，铁丝的长为 x cm，做成圆的半径为 y cm；④在水龙头前放满一桶水，出水的速度为 x，放满一桶水的时间 y.A. 1个 B. 2个 C. 3个 D. 4个
A. B. C. D.
2. 下列函数中，y是x的反比例函数的是 ( )
3. 填空 (1) 若 是反比例函数，则 m 的取值范围 是 . (2) 若 是反比例函数，则m的取值范 围是 . (3) 若 是反比例函数，则m的取值范围 是 .
m ≠ 0 且 m ≠ －2
4. 已知 y 与 x+1 成反比例，并且当 x = 3 时，y = 4.
(1) 写出 y 关于 x 的函数解析式； (2) 当 x = 7 时，求 y 的值．
5. 小明家离学校 1000 m，每天他往返于两地之间，有 时步行，有时骑车．假设小明每天上学时的平均速 度为 v ( m/min )，所用的时间为 t ( min )． (1) 求变量 v 和 t 之间的函数关系式；
(2) 小明星期二步行上学用了 25 min，星期三骑自行 车上学用了 8 min，那么他星期三上学时的平均 速度比星期二快多少？
125－40＝85 ( m/min )．答：他星期三上学时的平均速度比星期二快 85 m/min.
6. 已知 y = y1+y2，y1与 (x－1) 成正比例，y2 与 (x + 1) 成反比例，当 x = 0 时，y =－3；当 x =1 时，y = －1， 求：
(1) y 关于 x 的关系式；
∵ x = 0 时，y =－3；x =1 时，y = －1，
－3=－k1+k2 ，
∴k1=1，k2=－2.
用待定系数法求反比例函数解析式
反比例函数：定义/三种表达方式