高考数学一轮复习第6章不等式第2讲一元二次不等式及其解法 学案

这是一份高考数学一轮复习第6章不等式第2讲一元二次不等式及其解法 学案，共12页。

知识梳理·双基自测
eq \x(知)eq \x(识)eq \x(梳)eq \x(理)
知识点一 一元二次不等式的解法
(1)将不等式的右边化为零，左边化为二次项系数_大于__零的不等式ax2＋bx＋c>0(a>0)或ax2＋bx＋c<0(a>0)．
(2)计算相应的_判别式__.
(3)当_Δ≥0__时，求出相应的一元二次方程的根．
(4)利用二次函数的图象与x轴的_交点__确定一元二次不等式的解集．
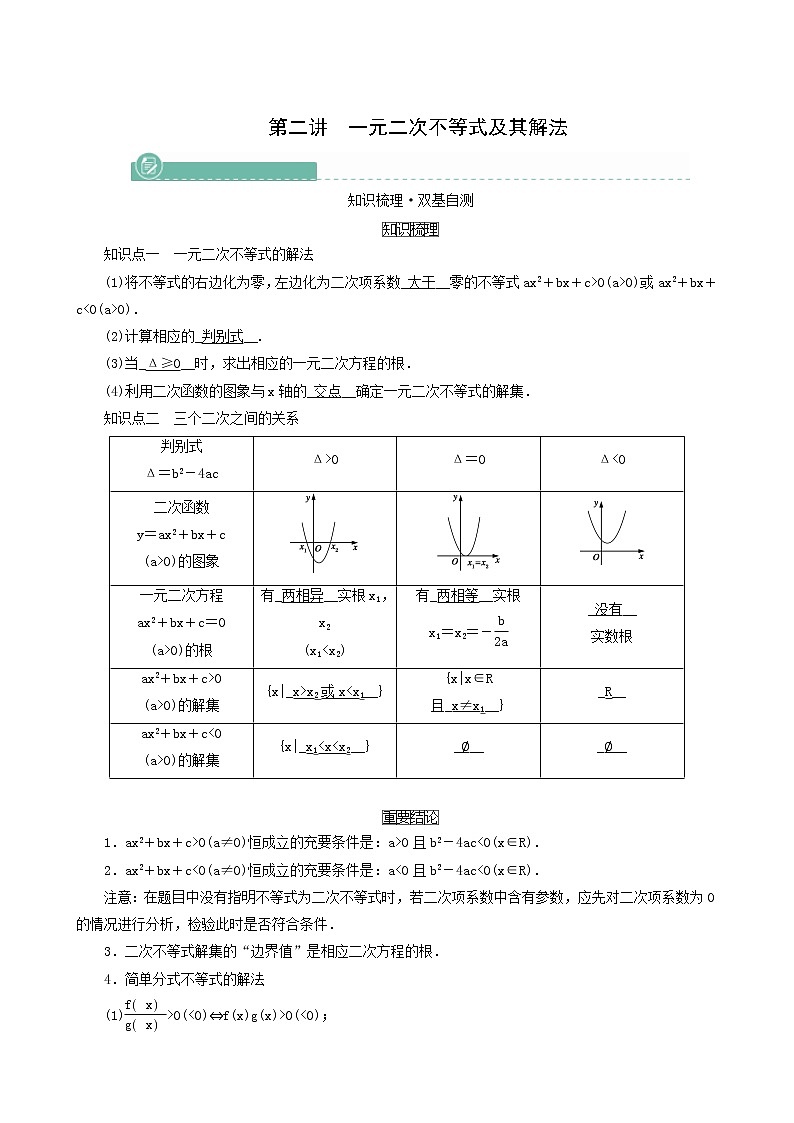
知识点二 三个二次之间的关系
eq \x(重)eq \x(要)eq \x(结)eq \x(论)
1．ax2＋bx＋c>0(a≠0)恒成立的充要条件是：a>0且b2－4ac<0(x∈R)．
2．ax2＋bx＋c<0(a≠0)恒成立的充要条件是：a<0且b2－4ac<0(x∈R)．
注意：在题目中没有指明不等式为二次不等式时，若二次项系数中含有参数，应先对二次项系数为0的情况进行分析，检验此时是否符合条件．
3．二次不等式解集的“边界值”是相应二次方程的根．
4．简单分式不等式的解法
(1)eq \f(fx,gx)>0(<0)⇔f(x)g(x)>0(<0)；
(2)eq \f(fx,gx)≥0(≤0)⇔eq \b\lc\{\rc\ (\a\vs4\al\c1(fx·gx≥0≤0,gx≠0)).
5．简单的指数与对数不等式的解法
(1)若a>1，af(x)>ag(x)⇔f(x)>g(x)；
若0ag(x)⇔f(x)(2)若a>1，lgaf(x)>lgag(x)⇔f(x)>g(x)>0；
若0lgag(x)⇔0eq \x(双)eq \x(基)eq \x(自)eq \x(测)
题组一 走出误区
1．判断下列结论是否正确(请在括号中打“√”或“×”)
(1)若不等式ax2＋bx＋c<0的解集为(x1，x2)，则必有a>0.( √ )
(2)若不等式ax2＋bx＋c>0的解集是(－∞，x1)∪(x2，＋∞)，则方程ax2＋bx＋c＝0的两个根是x1和x2.( √ )
(3)若方程ax2＋bx＋c＝0(a≠0)没有实数根，则不等式ax2＋bx＋c>0的解集为R.( × )
(4)不等式ax2＋bx＋c≤0在R上恒成立的条件是a<0且Δ＝b2－4ac≤0.( × )
(5)若二次函数y＝ax2＋bx＋c的图象开口向下，则不等式ax2＋bx＋c<0的解集一定不是空集．( √ )
题组二 走进教材
2．(必修5P26T2改编)不等式x(1－2x)>0的解集是( B )
A．eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1,2))) B．eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,2)))
C．(－∞，0)∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞)) D．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞))
3．(必修5P80A组T4改编)已知集合A＝{x|x2－x－6>0}，则∁RA等于( B )
A．{x|－2C．{x|x<－2}∪{x|x>3} D．{x|x≤－2}∪{x|x≥3}
[解析] ∵x2－x－6>0，∴(x＋2)(x－3)>0，
∴x>3或x<－2，即A＝{x|x>3或x<－2}．
在数轴上表示出集合A，如图所示．
由图可得∁RA＝{x|－2≤x≤3}．故选B．
4．(必修5P80A组T2改编)y＝lg2(3x2－2x－2)的定义域是_eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1－\r(7),3)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1＋\r(7),3)，＋∞))__.
[解析] 由题意，得3x2－2x－2>0，
令3x2－2x－2＝0，得x1＝eq \f(1－\r(7),3)，x2＝eq \f(1＋\r(7),3)，
∴3x2－2x－2>0的解集为eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1－\r(7),3)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1＋\r(7),3)，＋∞)).
题组三 走向高考
5．(2019·天津高考)设x∈R，使不等式3x2＋x－2<0成立的x的取值范围是_eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(2,3)))__.
[解析] 3x2＋x－2<0⇒(x＋1)(3x－2)<0，
⇒(x＋1)eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(2,3)))<0⇒－1∴x的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(2,3))).
考点突破·互动探究
考点一 一元二次不等式的解法——多维探究
角度1 不含参数的不等式
例1 解下列不等式
(1)－2x2＋x＋3<0；
(2)x2－2x＋2>0.
[分析] (1)将二次项系数化为正数，变为2x2－x－3>0，求方程2x2－x－3＝0的根，若无根，则解集为R，若有根，则按“小于取中间，大于取两边”写出解集．
[解析] (1)化－2x2＋x＋3<0为2x2－x－3>0，
∴(x＋1)(2x－3)>0，即(x＋1)eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(3,2)))>0，
∴x>eq \f(3,2)或x<－1，
∴原不等式的解集为(－∞，－1)∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)，＋∞)).
(2)因为Δ<0，所以方程x2－2x＋2＝0无实数解，而y＝x2－2x＋2的图象开口向上，可得原不等式x2－2x＋2>0的解集为R.
名师点拨
解一元二次不等式的一般步骤
(1)化：把不等式变形为二次项系数大于零的标准形式．
(2)判：计算对应方程的判别式．
(3)求：求出对应的一元二次方程的根，或根据判别式说明方程有没有实根．
(4)写：利用“大于取两边，小于取中间”写出不等式的解集．
角度2 含参数的不等式
例2 解下列关于x的不等式：
(1)ax2－(a＋1)x＋1<0(a∈R)；
(2)x2－2ax＋2≤0(a∈R)；
[分析] (1)因二次项系数含有字母，故需对其符号分类求解，即讨论a与0的关系，并注意根的大小关系，即讨论eq \f(1,a)与1的关系，故需分a<0，a＝0,01五种情况求解；
(2)由于系数中含有字母，故需考虑对应的方程有无实根，以及有根时根的大小关系；
[解析] (1)若a＝0，原不等式等价于－x＋1＜0，解得x＞1.
若a＜0，则原不等式等价于eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＞0，解得x＜eq \f(1,a)或x＞1.
若a＞0，原不等式等价于eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0.
①当a＝1时，eq \f(1,a)＝1，eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0无解；
②当a＞1时，eq \f(1,a)＜1，解eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0得eq \f(1,a)＜x＜1；
③当0＜a＜1时，eq \f(1,a)＞1，解eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0得1＜x＜eq \f(1,a).
综上所述：当a＜0时，解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x＜\f(1,a)或x＞1))))；当a＝0时，解集为{x|x＞1}；当0＜a＜1时，解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(1＜x＜\f(1,a)))))；当a＝1时，解集为∅；当a＞1时，解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(\f(1,a)＜x＜1)))).
(2)对于方程x2－2ax＋2＝0，因为Δ＝4a2－8，所以当Δ＜0，即－eq \r(2)＜a＜eq \r(2)时，x2－2ax＋2＝0无实根．又二次函数y＝x2－2ax＋2的图象开口向上，所以原不等式的解集为∅；
当Δ＝0，即a＝±eq \r(2)时，x2－2ax＋2＝0有两个相等的实根，
当a＝eq \r(2)时，原不等式的解集为{x|x＝eq \r(2)}，
当a＝－eq \r(2)时，原不等式的解集为{x|x＝－eq \r(2)}；
当Δ＞0，即a＞eq \r(2)或a＜－eq \r(2)时，x2－2ax＋2＝0有两个不相等的实根，分别为x1＝a－eq \r(a2－2)，x2＝a＋eq \r(a2－2)，且x1＜x2，所以原不等式的解集为{x|a－eq \r(a2－2)≤x≤a＋eq \r(a2－2)}．
综上，当a＞eq \r(2)或a＜－eq \r(2)时，解集为{x|a－eq \r(a2－2)≤x≤a＋eq \r(a2－2)}；当a＝eq \r(2)时，解集为{x|x＝eq \r(2)}；当a＝－eq \r(2)时，解集为{x|x＝－eq \r(2)}；当－eq \r(2)＜a＜eq \r(2)时，解集为∅.
名师点拨
含参数的不等式的求解往往需要分类讨论
(1)若二次项系数为常数，若判别式Δ≥0，可先考虑分解因式，再对根的大小分类讨论(分点由x1＝x2确定)；若不易分解因式，可考虑求根公式，以便写出解集，若Δ<0，则结合二次函数图象写出解集，若判别式符号不能确定，则需对判别式分类讨论(分点由Δ＝0确定)．
(2)若二次项系数为参数，则应先考虑二次项系数是否为零，然后讨论二次项系数大于零、小于零，以便确定解集形式．
(3)解简单分式不等式是通过移项、通分化为整式不等式求解，要注意分母不能为零．
(4)解简单的指数、对数不等式时，若底含有参数，则需对其是否大于1分类求解，注意对数的真数必须为正．
〔变式训练1〕
(1)(角度1)(2021·北京市海淀区期末)不等式x2＋2x－3<0的解集为( D )
A．{x|x<－3或x>1} B．{x|x<－1或x>3}
C．{x|－1(2)(角度2)解不等式x2－(a＋1)x＋a<0(a∈R)
[解析] (1)由x2＋2x－3<0得(x＋3)(x－1)<0，解得－3(2)由x2－(a＋1)x＋a＝0，得(x－a)(x－1)＝0，
∴x1＝a，x2＝1，
①当a>1时，x2－(a＋1)x＋a<0的解集为{x|1②当a＝1时，x2－(a＋1)x＋a<0的解集为∅，
③当a<1时，x2－(a＋1)x＋a<0的解集为{x|a考点二 三个二次间的关系——师生共研
例3 (1)(2021·黑龙江大庆实验中学期末)已知不等式ax2－bx－1>0的解集是eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(－\f(1,2)A．{x|2C．eq \b\lc\{\rc\ (\a\vs4\al\c1(x\b\lc\|\rc\}(\a\vs4\al\c1(\f(1,3)(2)若不等式x2＋ax－2>0在区间[1,5]上有解，则a的取值范围是( A )
A．eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)，＋∞)) B．eq \b\lc\(\rc\](\a\vs4\al\c1(－\f(23,5)，1))
C．(1，＋∞) D．eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(23,5)))
[分析] (1)利用根与系数的关系求解．
(2)令f(x)＝x2＋ax－2，Δ＝a2＋8>0恒成立，又两根之积为负值，所以只要f(1)≥0或f(1)<0且f(5)>0，于是得解；思路二：“正难则反”，求x2＋ax－2≤0在区间[1,5]上恒成立的a的取值集合，只需f(5)≤0，再求其补集即可；思路三：分离参数．
[解析] (1)∵不等式ax2－bx－1>0的解集是
eq \b\lc\{\rc\}(\a\vs4\al\c1(x|－\f(1,2)∴ax2－bx－1＝0的解是x1＝－eq \f(1,2)和x2＝－eq \f(1,3)，且a<0，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(1,2)－\f(1,3)＝\f(b,a)，,\b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))×\b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,3)))＝－\f(1,a)，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝－6，,b＝5.))
则不等式x2－bx－a≥0即为x2－5x＋6≥0，解得x≤2或x≥3.故选B．
(2)令f(x)＝x2＋ax－2，则Δ＝a2＋8>0，
∴方程f(x)＝0，有两个不等实根，又两根之积为负，
∴方程有一正根和一负根．
解法一：不等式x2＋ax－2>0在区间[1,5]上有解，只要f(1)≥0或eq \b\lc\{\rc\ (\a\vs4\al\c1(f1<0，,f5>0.))解得a≥1或－eq \f(23,5)∴a的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)，＋∞))，故选A．
解法二：不等式x2＋ax－2≤0在[1,5]上恒成立，只要f(5)≤0，即25＋5a－2≤0，解得a≤－eq \f(23,5)，∴不等式x2＋ax－2>0在区间[1,5]上有解的a的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)，＋∞)).
解法三：x2＋ax－2>0在区间[1,5]上有解⇔a>eq \f(2,x)－x在[1,5]上有解⇔a>f(x)min(记f(x)＝eq \f(2,x)－x，x∈[1,5])，显然f(x)为减函数，∴f(x)min＝f(5)＝－eq \f(23,5)，∴a>－eq \f(23,5).
[引申]若不等式x2＋ax－2<0在区间[1,5]上有解，则a的取值范围是_(－∞，1)__.
[解析] 由例3(2)的解析知，不等式x2＋ax－2<0在区间[1,5]上有解，a名师点拨
已知不等式的解集，等于知道了与之对应方程的根，此时利用韦达定理或判别式即可求出参数的值或范围，为简化讨论注意数形结合，如本例(2)中对应的二次函数图象过点(0，－2)．
〔变式训练2〕
(1)关于x的不等式x2－2ax－8a2<0(a>0)的解集为(x1，x2)，且x2－x1＝15，则a＝( A )
A．eq \f(5,2) B．eq \f(7,2)
C．eq \f(15,4) D．eq \f(15,2)
(2)(2021·九江模拟)若关于x的不等式x2－4x－2－a>0在区间(1,4)内有解，则实数a的取值范围是( A )
A．(－∞，－2) B．(－2，＋∞)
C．(－6，＋∞) D．(－∞，－6)
[解析] (1)解法一：由题意知x1，x2是方程x2－2ax－8a2＝0的两根，则x1＋x2＝2a，x1x2＝－8a2.又x2－x1＝15，∴(x2－x1)2＝(x1＋x2)2－4x1x2＝4a2＋32a2＝36a2＝152.∵a>0，∴a＝eq \f(15,6)＝eq \f(5,2)，故选A．
解法二：由x2－2ax－8a2＝(x＋2a)(x－4a)<0，∵a>0，∴不等式的解集为(－2a,4a)．
又不等式的解集为(x1，x2)，∴x1＝－2a，x2＝4a.∴x2－x1＝4a－(－2a)＝6a＝15，∴a＝eq \f(5,2)，故选A．
(2)解法一：由函数f(x)＝x2－4x－2－a图象的对称轴为x＝2.∴不等式x2－4x－2－a>0在区间(1,4)内有解⇔f(4)>0，即a<－2，故选A．
解法二：(分离参数法)不等式x2－4x－2－a>0在区间(1,4)内有解等价于a<(x2－4x－2)max，令g(x)＝x2－4x－2，x∈(1,4)，∴g(x)考点三 一元二次不等式恒成立问题——师生共研
例4 已知f(x)＝mx2－mx－1.
(1)若对于x∈R，f(x)<0恒成立，求实数m的取值范围；
(2)若对于x∈[1,3]，f(x)<－m＋5恒成立，求实数m的取值范围；
(3)若对于|m|≤1，f(x)<0恒成立，求实数x的取值范围．
[分析] (1)二次项系数含有字母m，应分m＝0和m≠0讨论求解；(2)数形结合，分类讨论；(3)把二次不等式转化为含m的一次不等式，根据一次函数的性质求解．
[解析] (1)要使mx2－mx－1<0恒成立，
若m＝0，显然－1<0；
若m≠0，则eq \b\lc\{\rc\ (\a\vs4\al\c1(m<0，,Δ＝m2＋4m<0))⇒－4所以m的取值范围为(－4,0]．
(2)要使f(x)<－m＋5在[1,3]上恒成立，
只需mx2－mx＋m<6恒成立(x∈[1,3])，
又因为x2－x＋1＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,2)))2＋eq \f(3,4)>0，
所以m因为t＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,2)))2＋eq \f(3,4)在[1,3]上是增函数，
所以y＝eq \f(6,x2－x＋1)在[1,3]上是减函数．
因此函数的最小值ymin＝eq \f(6,7).
所以m的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(6,7))).
(3)将不等式f(x)<0整理成关于m的不等式为(x2－x)m－1<0.
令g(m)＝(x2－x)m－1，m∈[－1,1]．
则eq \b\lc\{\rc\ (\a\vs4\al\c1(g－1<0，,g1<0))即eq \b\lc\{\rc\ (\a\vs4\al\c1(－x2＋x－1<0，,x2－x－1<0，))
解得eq \f(1－\r(5),2)即x的取值范围为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1－\r(5),2)，\f(1＋\r(5),2))).
名师点拨
一元二次不等式恒成立问题
1．在R上恒成立
(1)一元二次不等式ax2＋bx＋c>0(或≥0)对于一切x∈R恒成立的条件是eq \b\lc\{\rc\ (\a\vs4\al\c1(a>0，,Δ＝b2－4ac<0或≤0.))
(2)一元二次不等式ax2＋bx＋c<0(或≤0)对于一切x∈R恒成立的条件是eq \b\lc\{\rc\ (\a\vs4\al\c1(a<0，,Δ＝b2－4ac<0或≤0.))
2．在给定某区间上恒成立
(1)当x∈[m，n]，f(x)＝ax2＋bx＋c≥0恒成立，结合图象，只需f(x)min≥0即可；
(2)当x∈[m，n]，f(x)＝ax2＋bx＋c≤0恒成立，只需f(x)max≤0即可．
3．解决恒成立问题一定要搞清谁是自变量，谁是参数．一般地，知道谁的范围，谁就是自变量，求谁的范围，谁就是参数．
4．“不等式f(x)≥0有解(或解集不空)的参数m的取值集合”是“f(x)<0恒成立的参数m取值集合”的补集；“f(x)>0的解集为∅”即“f(x)≤0恒成立．”
注意：ax2＋bx＋c>0恒成立⇔eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝b＝0,c>0))或eq \b\lc\{\rc\ (\a\vs4\al\c1(a>0,Δ＝b2－4ac<0))；
ax2＋bx＋c<0恒成立⇔eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝b＝0,c<0))或eq \b\lc\{\rc\ (\a\vs4\al\c1(a<0,Δ＝b2－4ac<0)).
〔变式训练3〕
(1)若不等式(a－3)x2＋2(a－3)x－4<0对一切x∈R恒成立，则实数a取值的集合为( D )
A．(－∞，3) B．(－1,3)
C．[－1,3] D．(－1,3]
(2)(2021·山西忻州第一中学模拟)已知关于x的不等式x2－4x≥m对任意的x∈(0,1]恒成立，则有( A )
A．m≤－3 B．m≥－3
C．－3≤m<0 D．m≥－4
(3)已知对于任意的a∈[－1,1]，函数f(x)＝x2＋(a－4)x＋4－2a的值总大于0，则x的取值范围是( B )
A．{x|13}
C．{x|12}
[解析] (1)当a＝3时，－4<0恒成立；
当a≠3时，eq \b\lc\{\rc\ (\a\vs4\al\c1(a<3，,Δ＝4a－32＋16a－3<0，))
解得－1(2)令f(x)＝x2－4x，x∈(0,1]，∵f(x)图象的对称轴为直线x＝2，∴f(x)在(0,1]上单调递减，∴当x＝1时，f(x)取得最小值－3，∴m≤－3，故选A．
(3)记g(a)＝(x－2)a＋x2－4x＋4，a∈[－1,1]，
依题意，只须eq \b\lc\{\rc\ (\a\vs4\al\c1(g1>0，,g－1>0))⇒eq \b\lc\{\rc\ (\a\vs4\al\c1(x2－3x＋2>0，,x2－5x＋6>0))⇒x<1或x>3，故选B．
名师讲坛·素养提升
一元二次方程根的分布
设一元二次方程ax2＋bx＋c＝0(a≠0)，记f(x)＝ax2＋bx＋c.
(1)方程无根Δ＝b2－4ac<0；
(2)方程有两等根Δ＝b2－4ac＝0；
(3)方程有两不等实根Δ＝b2－4ac>0，记其根为x1，x2且x1①x1>0⇔eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ＝b2－4ac>0，,x1＋x2＝－\f(b,a)>0，,x1x2＝\f(c,a)>0.))或x1>0⇔eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,af0>0，,－\f(b,2a)>0；)) ②x1<00,x1x2＝\f(c,a)<0))或x1<00，,x1＋x2＝－\f(b,a)<0，,x1x2＝\f(c,a)>0，))或x10，,af0>0，,－\f(b,2a)<0.)) ④x2>x1>k⇔eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,afk>0，,－\f(b,2a)>k，)) ⑤x10，,afk>0，,－\f(b,2a)0，,afn<0；)) x10；)) m0，,afn>0，,m<－\f(b,2a)0.)) x1例5 若关于x的一元二次方程(m－1)x2＋2(m＋1)x－m＝0，分别满足下列条件时，求m的取值范围．
(1)一根在(1,2)内，另一根在(－1,0)内；
(2)一根在(－1,1)，另一根不在(－1,1)内；
(3)一根小于1，另一根大于2；
(4)一根大于－1，另一根小于－1；
(5)两根都在区间(－1,3)；
(6)两根都大于0；
(7)两根都小于1；
(8)在(1,2)内有解．
[解析] 设f(x)＝(m－1)x2＋2(m＋1)x－m，Δ＝4(m＋1)2＋4m(m－1)＝8m2＋4m＋4＝4(2m2＋m＋1)>0.
(1)一根在(1,2)内，另一根在(－1,0)内应满足eq \b\lc\{\rc\ (\a\vs4\al\c1(f1f2<0,f0f－1<0))即eq \b\lc\{\rc\ (\a\vs4\al\c1(m2m＋1<0,－2m－3－m<0))，解得－eq \f(1,2)(2)一根在(－1,1)内，另一根不在(－1,1)内，应满足f(－1)f(1)<0，即(2m＋1)(－2m－3)<0，∴m>－eq \f(1,2)或m<－eq \f(3,2)，又∵m－1≠0，∴m≠1，
∴m范围eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，－\f(3,2)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)，1))∪(1，＋∞)．
(3)一根小于1，另一根大于2，应满足eq \b\lc\{\rc\ (\a\vs4\al\c1(m－1f1<0,m－1f2<0))
即eq \b\lc\{\rc\ (\a\vs4\al\c1(m－12m＋1<0,m－1m<0))解得：0(4)一根大于－1，另一根小于－1，
应满足(m－1)f(－1)<0，即(m－1)(－2m－3)<0，
解得：m>1或m<－eq \f(3,2).
(5)两根都在(－1,3)内，应满足eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ≥0,－1<－\f(m＋1,m－1)<3,m－1f－1>0,m－1f3>0))，
解得：－eq \f(3,2)(6)两根都大于0，应满足
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ≥0,－\f(m＋1,m－1)>0,m－1f0>0))，解得：0(7)两根都小于1，应满足：eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ≥0,－\f(m＋1,m－1)<1,m－1f1>0))，
解得：m>1或m<－eq \f(1,2).
(8)在(1,2)内有解应满足eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ≥0,1<－\f(m＋1,m－1)<2,m－1f1>0,m－1f2>0))或f(1)f(2)≤0
解得－eq \f(1,2)≤m≤0，
经检验m＝－eq \f(1,2)及m＝0都不合题意舍去，
∴－eq \f(1,2)〔变式训练4〕
(1)(2021·山东实验中学诊断)如果方程x2＋(m－1)x＋m2－2＝0的两个实根一个小于1，另一个大于1，那么实数m的取值范围是_(－2,1)__.
(2)若方程x2＋(k＋2)x－k＝0的两实根均在区间(－1,1)内，则k的取值范围为_－4＋2eq \r(3)≤k<－eq \f(1,2)__.
[解析] (1)记f(x)＝x2＋(m－1)x＋m2－2，由题意可知f(1)＝m2＋m－2<0，解得－2(2)由题意得，eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ≥0，,－1<－\f(k＋2,2)<1，,f－1>0，,f1>0.))解得－4＋2eq \r(3)≤k<－eq \f(1,2).
判别式
Δ＝b2－4ac
Δ>0
Δ＝0
Δ<0
二次函数
y＝ax2＋bx＋c
(a>0)的图象
一元二次方程
ax2＋bx＋c＝0
(a>0)的根
有_两相异__实根x1，x2
(x1有_两相等__实根
x1＝x2＝－eq \f(b,2a)
_没有__
实数根
ax2＋bx＋c>0
(a>0)的解集
{x|_x>x2或x{x|x∈R
且_x≠x1__}
_R__
ax2＋bx＋c<0
(a>0)的解集
{x|_x1_∅__
_∅__