






高考数学二轮复习热点突破专题3立体几何第1讲空间几何体的表面积和体积课件
展开第1讲 空间几何体的表面积和体积
高考定位 简单几何体的表面积与体积计算,主要以选择题、填空题的形式呈现,在解答题中,有时与空间线、面位置证明相结合,面积与体积的计算作为其中的一问.
1.(2020·全国Ⅰ卷)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )
A.64π B.48π C.36π D.32π
2.(2020·全国Ⅲ卷)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.
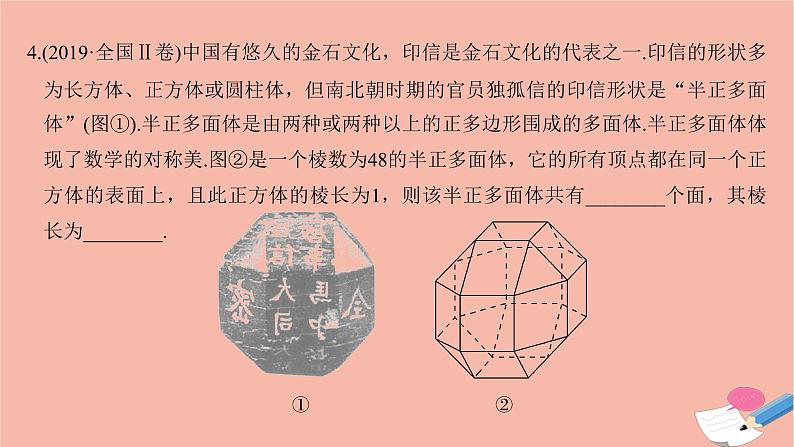
4.(2019·全国Ⅱ卷)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图①).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图②是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1,则该半正多面体共有________个面,其棱长为________.
1.空间几何体的两组常用公式
(1)柱体、锥体、台体、球的表面积公式:①圆柱的表面积S=2πr(r+l);②圆锥的表面积S=πr(r+l);③圆台的表面积S=π(r′2+r2+r′l+rl);④球的表面积S=4πR2.
答案 (1)B (2)AB
探究提高 1.求空间几何体的表面积,首先要掌握几何体的表面积公式,其次把不规则几何体分割成几个规则的几何体.2.(1)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(2)旋转体的表面积问题注意其侧面展开图的应用.
【训练1】 (1)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
(2)因为△ABC为等边三角形,边长为6,点A为CD的中点,所以AD=AB=6,所以△ADB为等腰三角形.又∠DAB=180°-∠CAB=120°,
探究提高 1.求三棱锥的体积:等体积转化是常用的方法,转换原则是其高易求,底面放在已知几何体的某一面上.2.求不规则几何体的体积:常用分割或补形的思想,将不规则几何体转化为规则几何体以易于求解.
【训练2】 (1)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
(2)(2020·东北三校一联)如图,四边形ABCD是边长为2的正方形,ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,则四面体ABEF的体积为( )
(2)∵ED⊥平面ABCD且AD⊂平面ABCD,∴ED⊥AD.∵在正方形ABCD中,AD⊥DC,而DC∩ED=D,∴AD⊥平面CDEF.
热点三 多面体与球的切、接问题【例3】 (1)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
(2)在《九章算术》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称之为阳马.如图,若四棱锥P-ABCD为阳马,侧棱PA⊥底面ABCD,且PA=3,BC=AB=4,设该阳马的外接球半径为R,内切球半径为r,则R=________;内切球的体积V=________.
解析 (1)由AB⊥BC,AB=6,BC=8,得AC=10.要使球的体积V最大,则球与直三棱柱的部分面相切,若球与三个侧面相切,设底面△ABC的内切圆的半径为r.
∴2r=4>3不合题意.球与三棱柱的上、下底面相切时,球的半径R最大.
探究提高 1.与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.2.若球面上四点P,A,B,C且PA,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.
高考数学二轮复习热点突破专题3立体几何规范答题示范课_立体几何解答题课件: 这是一份高考数学二轮复习热点突破专题3立体几何规范答题示范课_立体几何解答题课件,共10页。PPT课件主要包含了满分体验等内容,欢迎下载使用。
高考数学二轮复习热点突破专题6函数与导数第1讲函数图象与性质课件: 这是一份高考数学二轮复习热点突破专题6函数与导数第1讲函数图象与性质课件,共37页。PPT课件主要包含了真题感悟,答案D,考点整合,函数的图象,函数的性质等内容,欢迎下载使用。
高考数学二轮复习热点突破专题5解析几何第3讲圆锥曲线中的热点问题课件: 这是一份高考数学二轮复习热点突破专题5解析几何第3讲圆锥曲线中的热点问题课件,共52页。PPT课件主要包含了真题感悟,答案B,考点整合等内容,欢迎下载使用。












