

2022年河南省中考数学试卷
展开2022年河南省中考数学试卷
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.的相反数是
A. B.2 C. D.
2.2022年北京冬奥会的奖牌“同心”表达了“天地合人心同”的中华文化内涵.将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是
A.合 B.同 C.心 D.人
3.如图,直线,相交于点,,垂足为.若,则的度数为
A. B. C. D.
4.下列运算正确的是
A. B. C. D.
5.如图,在菱形中,对角线,相交于点,点为的中点.若,则菱形的周长为
A.6 B.12 C.24 D.48
6.一元二次方程的根的情况是
A.有两个不相等的实数根 B.没有实数根
C.有两个相等的实数根 D.只有一个实数根
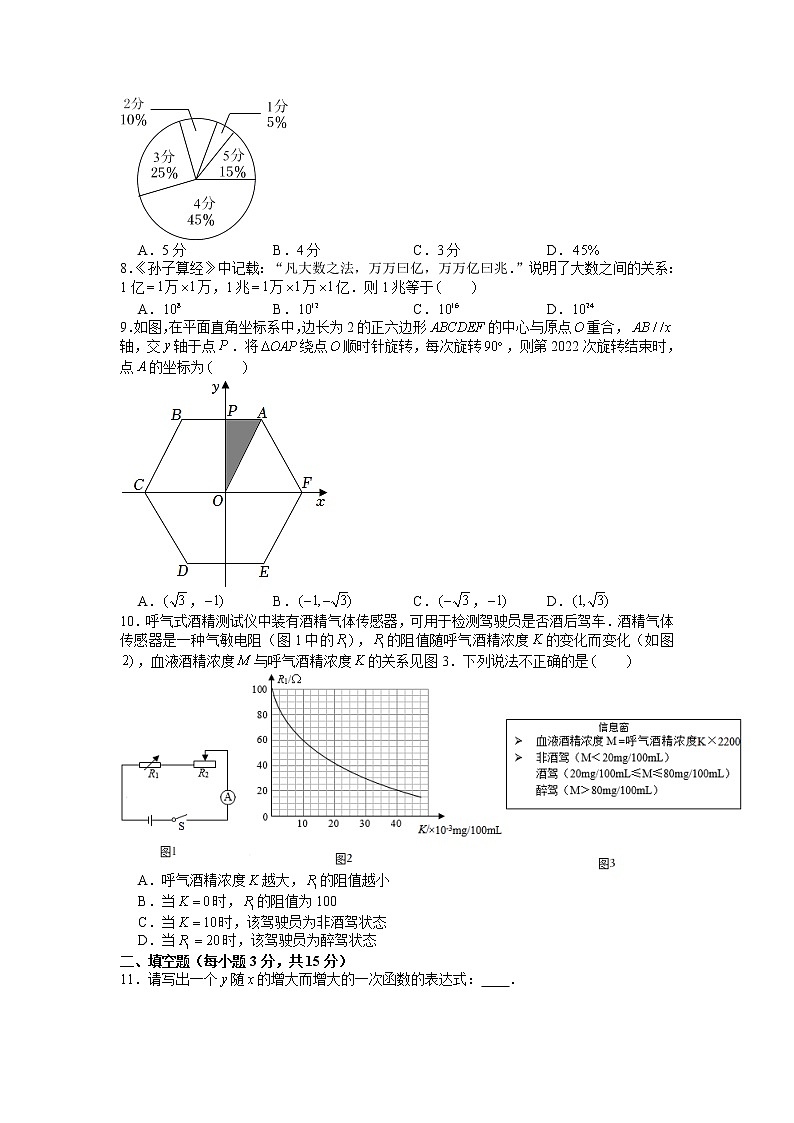
7.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为
A.5分 B.4分 C.3分 D.
8.《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿曰兆.”说明了大数之间的关系:1亿万万,1兆万万亿.则1兆等于
A. B. C. D.
9.如图,在平面直角坐标系中,边长为2的正六边形的中心与原点重合,轴,交轴于点.将绕点顺时针旋转,每次旋转,则第2022次旋转结束时,点的坐标为
A., B. C., D.
10.呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的,的阻值随呼气酒精浓度的变化而变化(如图,血液酒精浓度与呼气酒精浓度的关系见图3.下列说法不正确的是
A.呼气酒精浓度越大,的阻值越小
B.当时,的阻值为100
C.当时,该驾驶员为非酒驾状态
D.当时,该驾驶员为醉驾状态
二、填空题(每小题3分,共15分)
11.请写出一个随的增大而增大的一次函数的表达式: .
12.不等式组的解集为 .
13.为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率为 .
14.如图,将扇形沿方向平移,使点移到的中点处,得到扇形.若,,则阴影部分的面积为 .
15.如图,在中,,,点为的中点,点在上,且,将绕点在平面内旋转,点的对应点为点,连接,.当时,的长为 .
三、解答题(本大题共8个小题,共75分)
16.(10分)(1)计算:;
(2)化简:.
17.(9分)2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课,这是中国空间站的第二次太空授课,被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
.成绩频数分布表:
成绩(分
频数
7
9
12
16
6
.成绩在这一组的是(单位:分)
70 71 72 72 74 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)在这次测试中,成绩的中位数是 分,成绩不低于80分的人数占测试人数的百分比为 .
(2)这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.
(3)请对该校学生“航空航天知识”的掌握情况作出合理的评价.
18.(9分)如图,反比例函数的图象经过点和点,点在点的下方,平分,交轴于点.
(1)求反比例函数的表达式.
(2)请用无刻度的直尺和圆规作出线段的垂直平分线.(要求:不写作法,保留作图痕迹)
(3)线段与(2)中所作的垂直平分线相交于点,连接.求证:.
19.(9分)开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁的高度,如图,在处用测角仪测得拂云阁顶端的仰角为,沿方向前进到达处,又测得拂云阁顶端的仰角为.已知测角仪的高度为,测量点,与拂云阁的底部在同一水平线上,求拂云阁的高度(结果精确到.参考数据:,,.
20.(9分)近日,教育部印发《义务教育课程方案》和课程标准年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆种菜苗的价格是菜苗基地的倍,用300元在市场上购买的种菜苗比在菜苗基地购买的少3捆.
(1)求菜苗基地每捆种菜苗的价格.
(2)菜苗基地每捆种菜苗的价格是30元.学校决定在菜苗基地购买,两种菜苗共100捆,且种菜苗的捆数不超过种菜苗的捆数.菜苗基地为支持该校活动,对,两种菜苗均提供九折优惠.求本次购买最少花费多少钱.
21.(9分)小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头距地面,水柱在距喷水头水平距离处达到最高,最高点距地面;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头水平距离.身高的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
22.(10分)为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环与水平地面相切于点,推杆与铅垂线的夹角为,点,,,,在同一平面内.当推杆与铁环相切于点时,手上的力量通过切点传递到铁环上,会有较好的启动效果.
(1)求证:.
(2)实践中发现,切点只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点是该区域内最低位置,此时点距地面的距离最小,测得.已知铁环的半径为,推杆的长为,求此时的长.
23.(10分)(2022河南)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片,使与重合,得到折痕,把纸片展平;
操作二:在上选一点,沿折叠,使点落在矩形内部点处,把纸片展平,连接,.
根据以上操作,当点在上时,写出图1中一个的角: .
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片按照(1)中的方式操作,并延长交于点,连接.
①如图2,当点在上时, , ;
②改变点在上的位置(点不与点,重合),如图3,判断与的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片的边长为,当时,直接写出的长.
2022年河南省中考数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.的相反数是
A. B.2 C. D.
【分析】直接利用相反数的定义得出即可.
【解答】解:的相反数是:.
故选:.
2.2022年北京冬奥会的奖牌“同心”表达了“天地合人心同”的中华文化内涵.将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是
A.合 B.同 C.心 D.人
【分析】根据正方体的表面展开图找相对面的方法,一线隔一个,即可解答.
【解答】解:在原正方体中,与“地”字所在面相对的面上的汉字是人,
故选:.
3.如图,直线,相交于点,,垂足为.若,则的度数为
A. B. C. D.
【分析】首先利用垂直的定义得到,然后利用平角的定义即可求解.
【解答】解:,
,
,
.
故选:.
4.下列运算正确的是
A. B. C. D.
【分析】利用二次根式的减法的法则,完全平方公式,幂的乘方的法则,单项式乘单项式的法则对各项进行运算即可.
【解答】解:、,故不符合题意;
、,故不符合题意;
、,故不符合题意;
、,故符合题意.
故选:.
5.如图,在菱形中,对角线,相交于点,点为的中点.若,则菱形的周长为
A.6 B.12 C.24 D.48
【分析】由菱形的性质可得出,,再根据直角三角形斜边上的中线等于斜边的一半得出的长,结合菱形的周长公式即可得出结论.
【解答】解:四边形为菱形,
,,
为直角三角形.
,点为线段的中点,
.
.
故选:.
6.一元二次方程的根的情况是
A.有两个不相等的实数根 B.没有实数根
C.有两个相等的实数根 D.只有一个实数根
【分析】根据根的判别式进行判断即可.
【解答】解:在一元二次方程中,
,,,
△,
原方程有两个不相等的实数根.
故选:.
7.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为
A.5分 B.4分 C.3分 D.
【分析】根据众数的定义求解即可.
【解答】解:由扇形统计图知,得4分的人数占总人数的,人数最多,
所以所打分数的众数为4分,
故选:.
8.《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿曰兆.”说明了大数之间的关系:1亿万万,1兆万万亿.则1兆等于
A. B. C. D.
【分析】根据同底数幂的乘法先求出1亿,再求1兆即可.
【解答】解:1亿
,
1兆
,
故选:.
9.如图,在平面直角坐标系中,边长为2的正六边形的中心与原点重合,轴,交轴于点.将绕点顺时针旋转,每次旋转,则第2022次旋转结束时,点的坐标为
A., B. C., D.
【分析】由正六边形的性质可得,再根据由可知,每4次为一个循环,由,可知点与点重合,求出点的坐标可得答案.
【解答】解:边长为2的正六边形的中心与原点重合,
,,
轴,
,
,
,,
,
将绕点顺时针旋转,每次旋转,可知点与重合,
由可知,每4次为一个循环,
,
点与点重合,
点与点关于原点对称,
,
第2022次旋转结束时,点的坐标为,
故选:.
10.呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的,的阻值随呼气酒精浓度的变化而变化(如图,血液酒精浓度与呼气酒精浓度的关系见图3.下列说法不正确的是
A.呼气酒精浓度越大,的阻值越小
B.当时,的阻值为100
C.当时,该驾驶员为非酒驾状态
D.当时,该驾驶员为醉驾状态
【分析】观察图2可直接判断、,由可算出的值,从而判断,观察图2可得时的值,从而算出的值,即可判断.
【解答】解:由图2可知,呼气酒精浓度越大,的阻值越小,故正确,不符合题意;
由图2知,时,的阻值为100,故正确,不符合题意;
由图3知,当时,,
当时,该驾驶员为酒驾状态,故不正确,符合题意;
由图2知,当时,,
,
该驾驶员为醉驾状态,故正确,不符合题意;
故选:.
二、填空题(每小题3分,共15分)
11.请写出一个随的增大而增大的一次函数的表达式: 答案不唯一,如 .
【分析】根据一次函数的性质只要使一次项系数大于0即可.
【解答】解:例如:,或等,答案不唯一.
12.不等式组的解集为 .
【分析】先解出每个不等式的解集,即可得到不等式组的解集.
【解答】解:,
解不等式①,得:,
解不等式②,得:,
该不等式组的解集是,
故答案为:.
13.为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率为 .
【分析】画树状图,共有12种可能的结果,其中恰好选中甲和丙的结果有2种,再由概率公式求解即可.
【解答】解:画树状图如下:
共有12种可能的结果,其中恰好选中甲和丙的结果有2种,
恰好选中甲和丙的概率为,
故答案为:.
14.如图,将扇形沿方向平移,使点移到的中点处,得到扇形.若,,则阴影部分的面积为 .
【分析】如图,设交于点,连接.首先证明,根据求解即可.
【解答】解:如图,设交于点,连接.
,,
,
,
,,
.
故答案为:.
15.如图,在中,,,点为的中点,点在上,且,将绕点在平面内旋转,点的对应点为点,连接,.当时,的长为 或 .
【分析】分两种情况:当点在上,当点在的延长线上,利用勾股定理分别进行计算即可解答.
【解答】解:如图:
,,
,
点为的中点,
,,
,
点、、在同一条直线上,
由旋转得:
,
分两种情况:
当点在上,
在中,,
,
当点在的延长线上,
在中,,
,
综上所述:当时,的长为或,
故答案为:或.
三、解答题(本大题共8个小题,共75分)
16.(10分)(1)计算:;
(2)化简:.
【分析】(1)先算立方根、零指数幂、负整数指数幂,再算加减;
(2)先通分,把除化为乘,再分解因式约分.
【解答】解:(1)原式
;
(2)原式
.
17.(9分)2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课,这是中国空间站的第二次太空授课,被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
.成绩频数分布表:
成绩(分
频数
7
9
12
16
6
.成绩在这一组的是(单位:分)
70 71 72 72 74 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)在这次测试中,成绩的中位数是 78.5 分,成绩不低于80分的人数占测试人数的百分比为 .
(2)这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.
(3)请对该校学生“航空航天知识”的掌握情况作出合理的评价.
【分析】(1)根据中位数的定义求解即可,用不低于80分的人数除以被测试人数即可;
(2)根据中位数的意义求解即可;
(3)答案不唯一,合理均可.
【解答】解:(1)这次测试成绩的中位数是第25、26个数据的平均数,而第25、26个数据分别为(分,
所以这组数据的中位数是78.5分,
成绩不低于80分的人数占测试人数的百分比为,
故答案为:78.5,;
(2)不正确,
因为甲的成绩77分低于中位数78.5分,
所以甲的成绩不可能高于一半学生的成绩;
(3)测试成绩不低于80分的人数占测试人数的,说明该校学生对“航空航天知识”的掌握情况较好(答案不唯一,合理均可).
18.(9分)如图,反比例函数的图象经过点和点,点在点的下方,平分,交轴于点.
(1)求反比例函数的表达式.
(2)请用无刻度的直尺和圆规作出线段的垂直平分线.(要求:不写作法,保留作图痕迹)
(3)线段与(2)中所作的垂直平分线相交于点,连接.求证:.
【分析】(1)直接把点的坐标代入求出即可;
(2)利用尺规作出线段的垂直平分线即可;
(3)证明,可得结论.
【解答】(1)解:反比例函数的图象经过点,
,
反比例函数的解析式为;
(2)解:如图,直线即为所求.
(3)证明:平分,
,
直线垂直平分线段,
,
,
,
.
19.(9分)开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁的高度,如图,在处用测角仪测得拂云阁顶端的仰角为,沿方向前进到达处,又测得拂云阁顶端的仰角为.已知测角仪的高度为,测量点,与拂云阁的底部在同一水平线上,求拂云阁的高度(结果精确到.参考数据:,,.
【分析】延长交于点,根据题意可得:,米,米,设米,在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义列出关于的方程,进行计算即可解答.
【解答】解:延长交于点,
由题意得:
,米,米,
设米,
米,
在中,,
(米,
在中,,
,
,
经检验:是原方程的根,
(米,
拂云阁的高度约为32米.
20.(9分)近日,教育部印发《义务教育课程方案》和课程标准年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆种菜苗的价格是菜苗基地的倍,用300元在市场上购买的种菜苗比在菜苗基地购买的少3捆.
(1)求菜苗基地每捆种菜苗的价格.
(2)菜苗基地每捆种菜苗的价格是30元.学校决定在菜苗基地购买,两种菜苗共100捆,且种菜苗的捆数不超过种菜苗的捆数.菜苗基地为支持该校活动,对,两种菜苗均提供九折优惠.求本次购买最少花费多少钱.
【分析】(1)设菜苗基地每捆种菜苗的价格是元,根据用300元在市场上购买的种菜苗比在菜苗基地购买的少3捆,列方程可得菜苗基地每捆种菜苗的价格是20元;
(2)设购买种菜苗捆,则购买种菜苗捆,根据种菜苗的捆数不超过种菜苗的捆数,得,设本次购买花费元,有,由一次函数性质可得本次购买最少花费2250元.
【解答】解:(1)设菜苗基地每捆种菜苗的价格是元,
根据题意得:,
解得,
经检验,是原方程的解,
答:菜苗基地每捆种菜苗的价格是20元;
(2)设购买种菜苗捆,则购买种菜苗捆,
种菜苗的捆数不超过种菜苗的捆数,
,
解得,
设本次购买花费元,
,
,
随的增大而减小,
时,取最小值,最小值为(元,
答:本次购买最少花费2250元.
21.(9分)小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头距地面,水柱在距喷水头水平距离处达到最高,最高点距地面;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头水平距离.身高的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
【分析】(1)由抛物线顶点,设抛物线的表达式为,用待定系数法可得抛物线的表达式为;
(2)当时,,解得或,即得她与爸爸的水平距离为或.
【解答】解:(1)由题意知,抛物线顶点为,
设抛物线的表达式为,将代入得:
,
解得,
,
答:抛物线的表达式为;
(2)当时,,
解得或,
她与爸爸的水平距离为或,
答:当她的头顶恰好接触到水柱时,与爸爸的水平距离是或.
22.(10分)为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环与水平地面相切于点,推杆与铅垂线的夹角为,点,,,,在同一平面内.当推杆与铁环相切于点时,手上的力量通过切点传递到铁环上,会有较好的启动效果.
(1)求证:.
(2)实践中发现,切点只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点是该区域内最低位置,此时点距地面的距离最小,测得.已知铁环的半径为,推杆的长为,求此时的长.
【分析】(1)本小题难度不大,方法颇多,方法1:如图1,过点作,分别交于点,交于点.首先证明,;再根据是切点得出.后面就很简单的证明出结论;方法2:如图2,延长交于点.因为为的切线,所以根据切线性质得到,,.再根据四边形、三角形的内角和即可证明;方法3:如图3,过点作,根据两直线平行,内错角相等和切线性质,可以很简单的证明问题;
(2)利用(1)中图1的辅助线即可解答.首先根据条件,,得到.再利用(1)证明出的,,能得到四边形为矩形,所以,从而得到.
【解答】证明:方法1:如图1,过点作,分别交于点,交于点.
与相切于点,
.
,
.
,
,
,,
为的切线,
.
,
.
,
,
;
方法2:如图2,延长交于点.
与相切于点,
,
,
,
.
为的切线,
,
.
在四边形中,.
,
.
;
方法3:如图3,过点作,
.
与相切于点,
,
,
.
,
,
.
为的切线,
,
,
.
(2)解:如图1,在中,
,,
.
由(1)知,,
,
在中,
,
,
.
,
.
,
四边形为矩形,
,
.
23.(10分)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片,使与重合,得到折痕,把纸片展平;
操作二:在上选一点,沿折叠,使点落在矩形内部点处,把纸片展平,连接,.
根据以上操作,当点在上时,写出图1中一个的角: 或或或(任写一个即可) .
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片按照(1)中的方式操作,并延长交于点,连接.
①如图2,当点在上时, , ;
②改变点在上的位置(点不与点,重合),如图3,判断与的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片的边长为,当时,直接写出的长.
【分析】(1)由折叠的性质可得,,,,由锐角三角函数可求,即可求解;
(2)①由“”可证,可得;
②由“”可证,可得;
(3)分两种情况讨论,由折叠的性质和勾股定理可求解.
【解答】解:(1)对折矩形纸片,
,,
沿折叠,使点落在矩形内部点处,
,,
,
,
,
,
故答案为:或或或(任写一个即可);
(2)①由(1)可知,
四边形是正方形,
,,
由折叠可得:,,
,,
又,
,
,
故答案为:15,15;
②,理由如下:
四边形是正方形,
,,
由折叠可得:,,
,,
又,
,
;
(3)由折叠的性质可得,,
,
,
当点在线段上时,,
,,
,
,
,
当点在线段上时,,
,,
,
,
,
综上所述:的长为或.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2022/6/28 20:40:21;用户:柯瑞;邮箱:ainixiaoke00@163.com;学号:500557
2012年河南省中考数学试卷及答案: 这是一份2012年河南省中考数学试卷及答案,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2011年河南省中考数学试卷及答案: 这是一份2011年河南省中考数学试卷及答案,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年河南省中考数学试卷: 这是一份2023年河南省中考数学试卷,共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












