

2021省哈尔滨宾县一中校高二下学期第二次月考数学(文)试卷含答案
展开
宾县一中2020-2021下学期第二次考试数学(文)试卷
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 复数( )
A. B. C. D.
2.已知集合,,则( )
A. B. C. D.
3.已知复数,则“”是“是纯虚数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.下列函数中,既是奇函数又是增函数的为( )
A. B. C. D.
5.函数的定义域为( )
A. B. C. D.
6. 阅读右面的程序框图,则输出的= ( )
A.14 B. 30 C. 20 D.55
7. 下面几种推理是合情推理的是 ( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°;
③三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得凸边形内角和是(-2)·180°;
④所有自然数都是整数,4是自然数,所以4是整数.
A.①④ B.②③ C.①②③ D.④
8.已知函数f(x)=则f[f(9)]=( )
A.- B. C.-8 D. 8
9. 观察按下列顺序排列的等式:,,,,猜想第个等式应为
A. B.
C. D.
10. 在极坐标系中,圆的圆心的极坐标是
A. B. C. D.
11.若函数则函数的图象关于( )
A.原点轴对称 B. 轴对称 C.轴对称 D. 对称
12.已知定义在R上的奇函数f(x)满足f(x+2)=f(x),且f(1)=0,当x∈(0,1)时,f(x)=2x+x.设a=f(5),,,则a,b,c的大小关系为( )
A.b>c>a B.a>c>b C.c>a>b D.b>a>c
二、填空题:(共4道题,每题5分,共20分)
13. 若函数,则 .
14.在复平面内,复数对应的点在直线上,则实数___________.
15. 设是周期为2的奇函数,当时,,则 .
16.给出下列命题:
①“若,则有实根”的逆否命题为真命题;
②命题“,”为真命题的一个充分不必要条件是;
③命题“,使得”的否定是真命题;
④命题:函数为偶函数;命题:函数在上为增函数,则为真命题.
其中正确命题的序号是__________.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17. (本小题满分12分)
设集合P={x∣-x2+x+6>0},Q={x∣a≤x≤a+3},其中aR.
(1)若a=1,求集合P (RQ);
(2)若P∪Q=P,求a的取值范围.
18.(本小题满分12分)
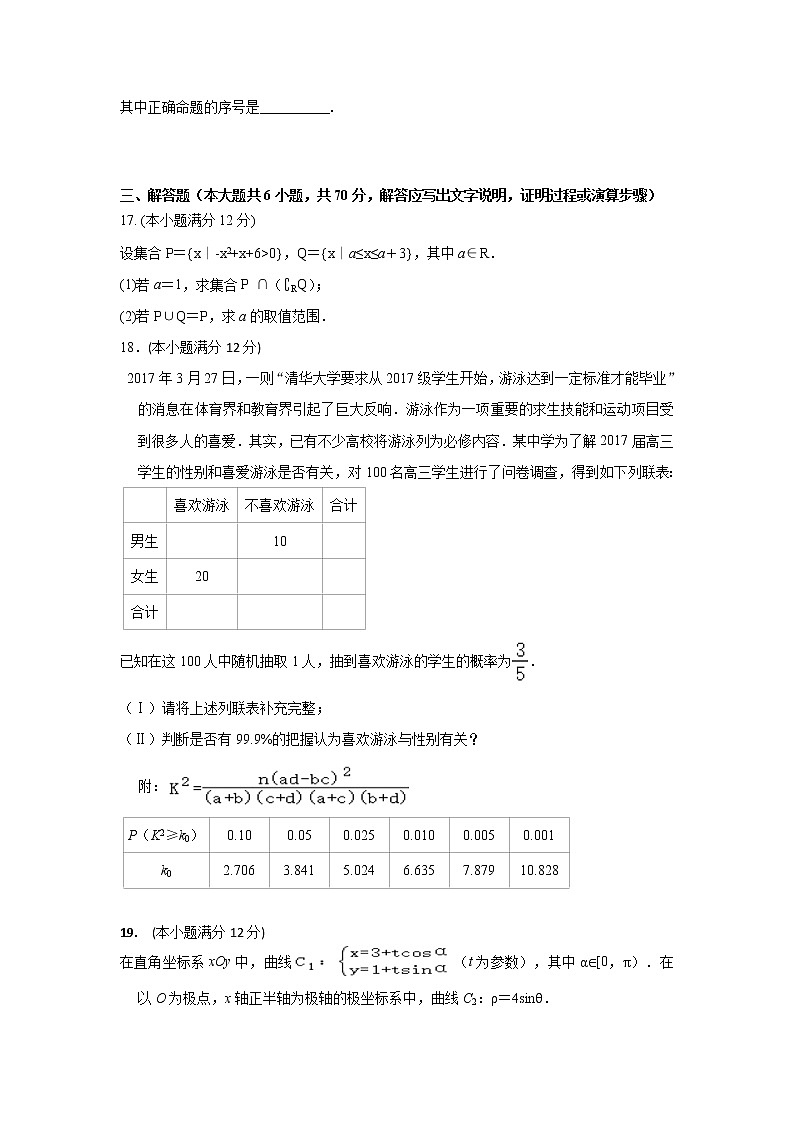
2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
| 喜欢游泳 | 不喜欢游泳 | 合计 |
男生 |
| 10 |
|
女生 | 20 |
|
|
合计 |
|
|
|
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19. (本小题满分12分)
在直角坐标系xOy中,曲线(t为参数),其中α∈[0,π).在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4sinθ.
(1)求C1的普通方程和C2的直角坐标方程;
(2)若C1与C2相交于点A,B两点,点P(3,1),求|PA|•|PB|.
20.(本小题满分12分)
已知函数f(x)=是定义域为R的奇函数.
(1)求实数a和b的值;
(2)若y=f(x)是在(1,+∞)上单调递减,且不等式f(t2-2t+3)+f(k-1)<0(k<0)对任意的t∈R恒成立,求实数k的取值范围.
21. (本小题满分12分)
已知函数.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)求函数的单调区间;
(Ⅲ)若对任意的,都有成立,求a的取值范围.
22.(本题满分10分)
在直角坐标系中,圆C的参数方程为为参数).以O为极点,轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线的极坐标方程是,射线OM:与圆的交点为,与直线的交点为,求线段的长.
宾县一中2020-2021下学期第二次考试
文科数学答案
一、选择题每小题5分,共60分
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | A | A | B | D | A | B | C | D | B | C | C | D |
二、填空题:每小题5分,共20分
13. 14.1 15. - 16. ①③
三、解答题(本大题共6小题,共70分,解答应写出文字说明)
17.(1)由题意知P={x∣-2<x<3}. ……………2分
因为a=1.所以Q={x∣1≤x≤4}.R Q={x∣x<1或x>4}.………3分
所以PR Q={x∣-2<x<1}. ………6分
(2) 由题意知QP. … …………7分
得-2<a<a+3<3. ……………10分
解得-2<a<0.综上,a的取值范围是(-2,0). ……………12分
18.解:(Ⅰ)因为在100人中随机抽取1人抽到喜欢游泳的学生的概率为,
所以喜欢游泳的学生人数为人;
其中女生有20人,男生有40人,列联表补充如下:
| 喜欢游泳 | 不喜欢游泳 | 合计 |
男生 | 40 | 10 | 50 |
女生 | 20 | 30 | 50 |
合计 | 60 | 40 | 100 |
…5分
(Ⅱ)因为K2=≈16.67>10.828;
所以有99.9%的把握认为喜欢游泳与性别有关. …12分.
19.解:(1)曲线(t为参数),转换为直角坐标方程为; ……4分
曲线C2:ρ=4sinθ,转换为直角坐标方程为:x2+(y﹣2)2=4,…………6分
(2)将曲线(t为参数)代入,
得(3+tcosα)2+(1+tsinα﹣2)2=4,
t2+(6cosα﹣2sinα)t+6=0, ……9分
设A,B两点对应的参数为t1,t2,
则|PA|•|PB|=|t1|•|t2|=|t1t2|=6,
∴|PA|•|PB|=6. …………12分
20.解:(1)∵f(x)=为奇函数,∴f(-x)=-f(x), …………1分
即=恒成立. …………2分
∴a=b=0, …………4分
∴f(x)=. …………5分
(2)∵f(x)为奇函数,∴f(t2-2t+3)+f(k-1)<0,
即f(t2-2t+3)<-f(k-1),等价于f(t2-2t+3)<f(1-k). …………7分
∵f(x)在(1,+∞)上为减函数,且t2-2t+3>1-k>1, …………9分
∴t2-2t+3>1-k.∴k>-(t-1)2-1. …………10分
∵t∈R,∴-(t-1)2-1≤-1, ∴k>-1 . …………11分
∵k<0, ∴k∈(-1,0). .…………12分
21.解:(Ⅰ)时,,,
,.
∴在点处的切线方程为. .…………4分
(Ⅱ).
①当时,恒成立,函数的递增区间为.
②当时,令,解得或.
x | |||
- | 0 | + | |
减 | 极小值 | 增 |
所以函数的递增区间为,递减区间为. .…………8分
(Ⅲ)①当时,在上是增函数,所以只需,
而,所以满足题意;
②当时,,在上是增函数,
所以只需.
而,所以满足题意;
③当时,,在上是减函数,上是增函数,
所以只需即可,而,
从而不满足题意;
综合①②③实数a的取值范围为.
.…………12分
22解:(1)圆C的参数方程(φ为参数).
消去参数可得:(x﹣1)2+y2=1.
把x=ρcosθ,y=ρsinθ代入化简得:ρ=2cosθ,
即为此圆的极坐标方程.…………5分
(2)因为,所以 …………10分
2021省哈尔滨宾县一中校高二下学期第一次月考数学(理)试卷含答案: 这是一份2021省哈尔滨宾县一中校高二下学期第一次月考数学(理)试卷含答案
2021省哈尔滨宾县一中校高二下学期第一次月考数学(文)试卷含答案: 这是一份2021省哈尔滨宾县一中校高二下学期第一次月考数学(文)试卷含答案
2021省哈尔滨宾县二中高二下学期第二次月考数学(理科)试题含答案: 这是一份2021省哈尔滨宾县二中高二下学期第二次月考数学(理科)试题含答案,共8页。试卷主要包含了用数学归纳法明,反证法证明命题,已知,设,则等内容,欢迎下载使用。












