2023年高考数学(文数)一轮复习课时40《简单几何体的表面积与体积》达标练习（2份，答案版+教师版）

这是一份2023年高考数学(文数)一轮复习课时40《简单几何体的表面积与体积》达标练习（2份，答案版+教师版），文件包含2023年高考数学文数一轮复习课时40《简单几何体的表面积与体积》达标练习含详解doc、2023年高考数学文数一轮复习课时40《简单几何体的表面积与体积》达标练习教师版doc等2份试卷配套教学资源，其中试卷共13页， 欢迎下载使用。

一、选择题
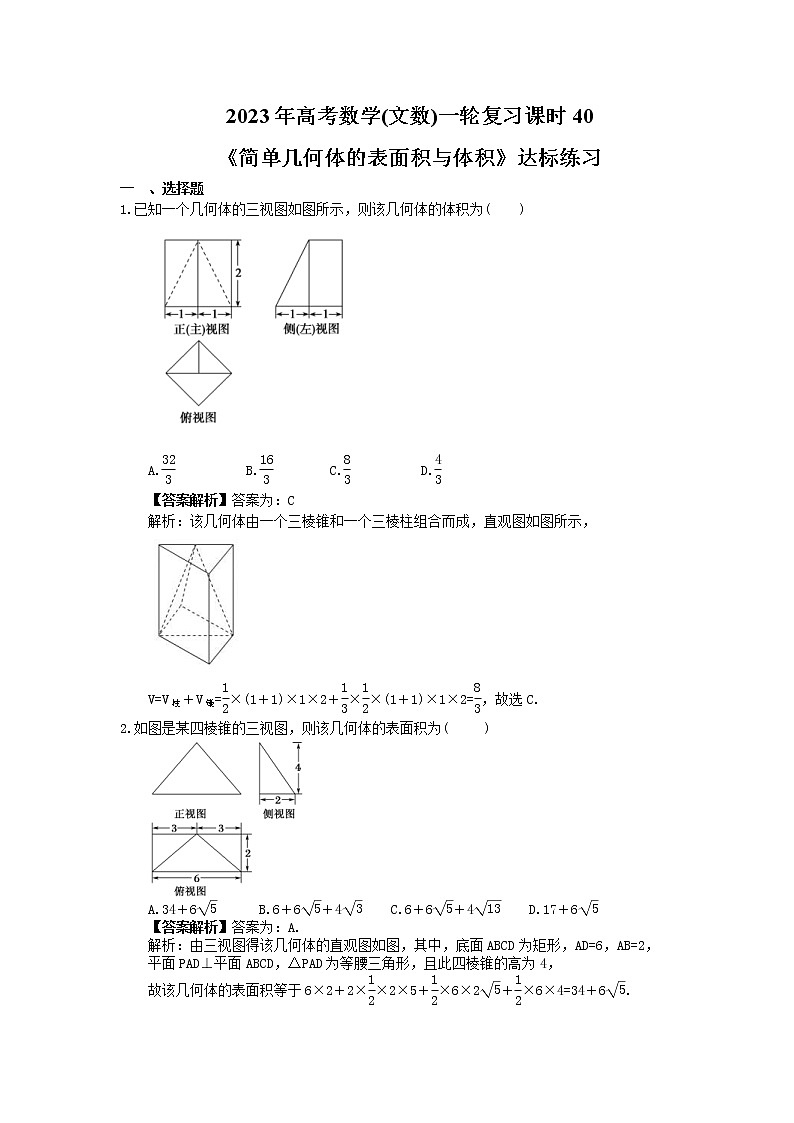
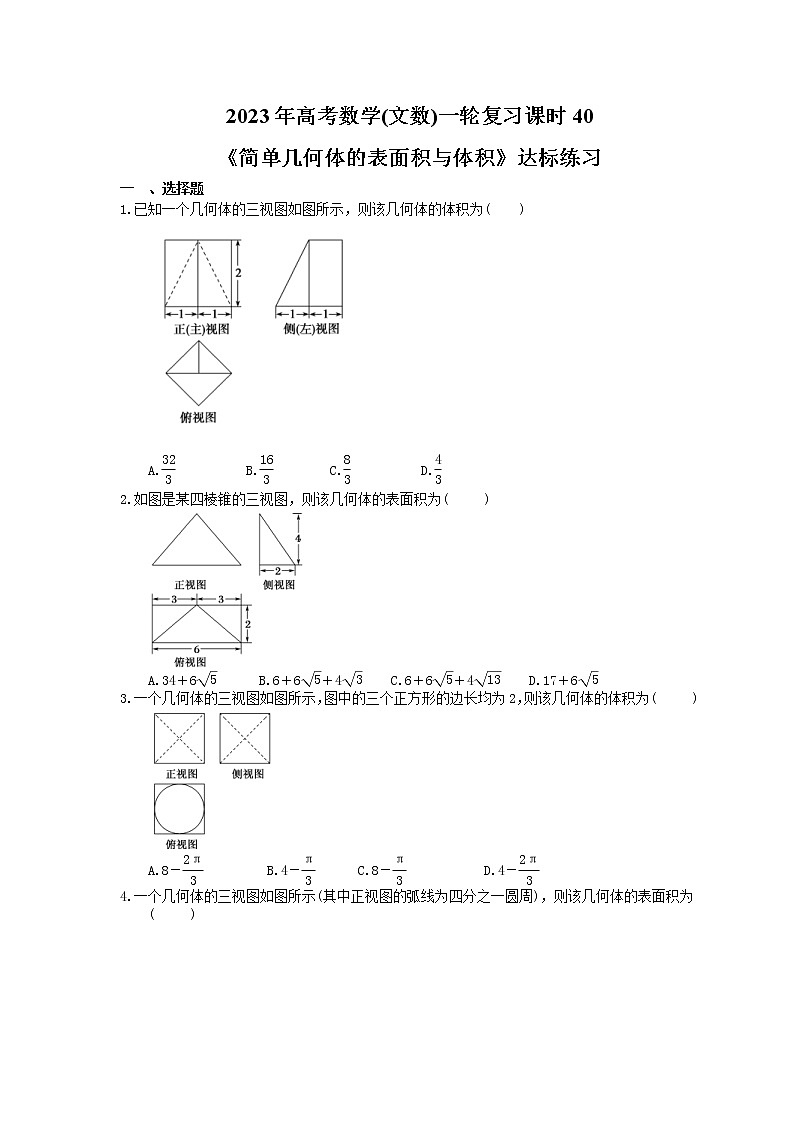
已知一个几何体的三视图如图所示，则该几何体的体积为( )
A.eq \f(32,3) B.eq \f(16,3) C.eq \f(8,3) D.eq \f(4,3)
【答案解析】答案为：C
解析：该几何体由一个三棱锥和一个三棱柱组合而成，直观图如图所示，
V=V柱＋V锥=eq \f(1,2)×(1＋1)×1×2＋eq \f(1,3)×eq \f(1,2)×(1＋1)×1×2=eq \f(8,3)，故选C.
如图是某四棱锥的三视图，则该几何体的表面积为( )
A.34＋6eq \r(5) B.6＋6eq \r(5)＋4eq \r(3) C.6＋6eq \r(5)＋4eq \r(13) D.17＋6eq \r(5)
【答案解析】答案为：A.
解析：由三视图得该几何体的直观图如图，其中，底面ABCD为矩形，AD=6，AB=2，
平面PAD⊥平面ABCD，△PAD为等腰三角形，且此四棱锥的高为4，
故该几何体的表面积等于6×2＋2×eq \f(1,2)×2×5＋eq \f(1,2)×6×2eq \r(5)＋eq \f(1,2)×6×4=34＋6eq \r(5).
一个几何体的三视图如图所示，图中的三个正方形的边长均为2，则该几何体的体积为( )
A.8－eq \f(2π,3) B.4－eq \f(π,3) C.8－eq \f(π,3) D.4－eq \f(2π,3)
【答案解析】答案为：A.
解析：由三视图可得该几何体的直观图如图所示，
该几何体是一个棱长为2的正方体上、下各挖去一个底面半径为1，
高为1的圆锥后剩余的部分，其体积为23－2×eq \f(1,3)×π×12×1=8－eq \f(2π,3).故选A.
一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周)，则该几何体的表面积为( )
A.72＋6π B.72＋4π C.48＋6π D.48＋4π
【答案解析】答案为：A.
解析：由三视图知，该几何体由一个正方体的eq \f(3,4)部分与一个圆柱的eq \f(1,4)部分组合而成(如图所示)，其表面积为16×2＋(16－4＋π)×2＋4×(2＋2＋π)=72＋6π.
将长、宽分别为4和3的长方形ABCD沿对角线AC折成直二面角，得到四面体A-BCD，
则四面体A-BCD的外接球的表面积为（ ）
A.25πB.50πC.5πD.10π
【答案解析】答案为：A
解析：取AC的中点，连接OB、OD，如下图所示：
由题意AC=5.
因为，O为AC的中点，所以，
所以，O为四面体A-BCD的外接球的球心，且球O的半径为R=2.5，
因此，四面体A-BCD的外接球的表面积为.
如图是一个四面体的三视图，这三个视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为( )
A.eq \f(2,3) B.eq \f(4,3) C.eq \f(8,3) D.2
【答案解析】答案为：A
解析：由三视图可知，此四面体如图所示，其高为2，底面三角形的一边长为1，
对应的高为2，所以其体积V=eq \f(1,3)×eq \f(1,2)×2×1×2=eq \f(2,3).故选A.
如图，在正四棱柱ABCD－A1B1C1D1中，点P是平面A1B1C1D1内一点，则三棱锥P－BCD的正(主)视图与侧(左)视图的面积之比为( )
A.1∶1 B.2∶1 C.2∶3 D.3∶2
【答案解析】答案为：A
解析：根据题意，三棱锥P－BCD的正视图是三角形，且底边为正四棱柱的底面边长，
高为正四棱柱的高；侧视图是三角形，且底边为正四棱柱的底面边长，
高为正四棱柱的高.故三棱锥P－BCD的正(主)视图与侧(左)视图的面积之比为1∶1.
如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体表面积为（ ）
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案解析】B.
解题思路：该几何体是棱长为2的正方体内的四面体 SKIPIF 1 < 0 . SKIPIF 1 < 0 的面积为2， SKIPIF 1 < 0 的面积均为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，故该四面体的表面积为 SKIPIF 1 < 0 ，故选B.
平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为eq \r(2)，则此球的体积为( )
A.eq \r(6)π B.4eq \r(3)π C.4eq \r(6)π D.6eq \r(3)π
【答案解析】答案为：B
解析：设球的半径为R，由球的截面性质得R=eq \r(\r(2)2＋12)=eq \r(3)，
所以球的体积V=eq \f(4,3)πR3=4eq \r(3)π.
已知三棱锥P­ABC中，AB=BC，AB⊥BC，点P在底面△ABC上的射影为AC的中点，若该三棱锥的体积为eq \f(9,2)，那么当该三棱锥的外接球体积最小时，该三棱锥的高为( )
A.2 B.3eq \r(3) C.2eq \r(3) D.3
【答案解析】答案为：D；
解析：设三棱锥P­ABC外接球的球心为O，△ABC的外接圆圆心为O1，
又AB⊥BC，所以O1为AC的中点.连接PO1，∵点P在底面△ABC上的射影为AC的中点，
∴PO1⊥平面ABC.∴P，O，O1三点共线.连接OB，O1B，
如图.由已知三棱锥P­ABC的底面△ABC为等腰直角三角形，设AB=a，三棱锥高PO1=h，
∴三棱锥P­ABC的体积V=eq \f(1,3)×eq \f(1,2)a2h=eq \f(9,2)，即a2=eq \f(27,h)，设OB=R，又OB2=BOeq \\al(2,1)＋OOeq \\al(2,1)，
∴R2=(eq \f(\r(2),2)a)2＋(h－R)2，∴R=eq \f(2h2＋a2,4h)=eq \f(h,2)＋eq \f(27,4h2)，由球O的体积V球=eq \f(4,3)πR3知，
当R最小时，其外接球体积最小，由R=eq \f(h,4)＋eq \f(h,4)＋eq \f(27,4h2)≥eq \f(9,4)，当且仅当eq \f(h,4)=eq \f(h,4)=eq \f(27,4h2)，
即h=3时取等号，因而三棱锥P­ABC的高为3时，外接球体积最小，故选D.
在三棱锥D­ABC中，已知AD⊥平面ABC，且△ABC为正三角形，AD=AB=eq \r(3)，点O为三棱锥D­ABC的外接球的球心，则点O到棱DB的距离为( )
A.eq \f(\r(42),14) B.eq \f(2\r(21),7) C.eq \f(1,4) D.eq \f(1,2)
【答案解析】答案为：D；
解析：设三棱锥D­ABC的外接球球心为O，过点O作DB的垂线，垂足为H，
作平面ODA交直线BC于点E，交eq \(BC,\s\up8(︵))于点F，设平面ODA截得外接球是⊙O，
D，A，F是⊙O表面上的点，又因为DA⊥平面ABC，所以∠DAF=90°，
E，所以DF是⊙O的直径，因此球心O在DF上，AF是三角形ABC外接圆的直径，
F，连接BD，BF，因为BF⊥DA，BF⊥AB，所以BF⊥平面DAB，
所以∠DBF=90°，因为∠DHO=90°，所以OH∥BF，又DO=OF，
所以OH是△DBF的中位线，OH=eq \f(1,2)BF，由AB=AD=eq \r(3)，三角形外接圆半径2R=eq \f(AB,sin A)，
得AF=2，在Rt△DAB中，DB=eq \r(AD2＋AB2)=eq \r(6)，
在Rt△DAF中，DF=eq \r(DA2＋AF2)=eq \r(7)，
在Rt△DBF中，BF=eq \r(DF2－DB2)=1，故OH=eq \f(1,2)，故选D.
已知四面体P­ABC的四个顶点都在球O的球面上，PA=8，BC=4，PB=PC=AB=AC，且平面PBC⊥平面ABC，则球O的表面积为( )
A.64π B.65π C.66π D.128π
【答案解析】答案为：B；
解析：如图，D，E分别为BC，PA的中点，易知球心O在线段DE上.
∵PB=PC=AB=AC，∴PD⊥BC，AD⊥BC，PD=AD.
又平面PBC⊥平面ABC，平面PBC∩平面ABC=BC，
∴PD⊥平面ABC.∴PD⊥AD.∴PD=AD=4eq \r(2).
∵点E是PA的中点，∴ED⊥PA，且DE=EA=PE=4.
设球O的半径为R，OE=x，则OD=4－x.在Rt△OEA中，有R2=16＋x2，
在Rt△OBD中，有R2=4＋(4－x)2，解得R2=eq \f(65,4)，所以S=4πR2=65π，故选B.
二、填空题
已知正四棱锥O-ABCD的体积为eq \f(3\r(2),2)，底面边长为eq \r(3)，则以O为球心，OA为半径的球的表面积为________.
【答案解析】答案为：24π
解析：过O作底面ABCD的垂线段OE(图略)，则E为正方形ABCD的中心.
由题意可知eq \f(1,3)×(eq \r(3))2×OE=eq \f(3\r(2),2)，所以OE=eq \f(3\r(2),2)，故球的半径R=OA= eq \r(OE2＋EA2)=eq \r(6)，
则球的表面积S=4πR2=24π.
已知一个正方体的所有顶点在一个球面上，若球的体积为eq \f(9π,2)，则正方体的棱长为______.
【答案解析】答案为：eq \r(3)
解析：设正方体棱长为a，球半径为R，则eq \f(4,3)πR3=eq \f(9π,2)，∴R=eq \f(3,2)，∴eq \r(3)a=3，∴a=eq \r(3).
如图，半球内有一内接正四棱锥S－ABCD，该四棱锥的体积为eq \f(4 \r(2),3)，则该半球的体积为________.
【答案解析】答案为：eq \f(4\r(2),3)π.
解析：设所给半球的半径为R，则棱锥的高h=R，底面正方形中有AB=BC=CD=DA=eq \r(2)R，
∴其体积为eq \f(2,3)R3=eq \f(4 \r(2),3)，则R3=2 eq \r(2)，于是所求半球的体积为V=eq \f(2,3)πR3=eq \f(4 \r(2),3)π.
已知某几何体的三视图如图，其中正视图中半圆直径为4，则该几何体的体积为________.
【答案解析】答案为：64－4π
解析：由三视图可知该几何体为一个长方体挖掉半个圆柱，
所以其体积为2×4×8－eq \f(1,2)×π×22×2=64－4π.