2022年山东省菏泽市重点中学中考数学模拟预测试卷（含答案）

2022年山东省菏泽市重点中学中考数学模拟预测试卷

注意：本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题，所有答案必须填在答题卷的相应位置。答案写在试卷上均无效，不予记分。

一、选择题（本大题共8小题，共24分）

1. 在这九个数中，无理数的个数为（　　）

A. 个 B. 个 C. 个 D. 个

2. 某种细菌的半径约为0000335厘米，将0000335这个数用科学记数法表示为（　　）

A.  B.  C.  D.

3. 下列几何图形中，主视图既是中心对称图形又是轴对称图形的有（　　）

A.  B.  C.  D.

4. 函数y=中x的取值范围是（　　）

A.  B.  C.  D.

5. 如图，在△ABC中，∠C=90°，BD平分∠ABC交AC于D，DE是AB的垂直平分线，若AD=3，则AC等于（　　）

A.
B.
C.
D.

6. 关于抛物线y=（x-1）2-2，下列说法错误的是（　　）

A. 顶点坐标为 B. 函数有最小值为
C. 开口方向向上 D. 当时，随的增大而减小

7. 如图，△ABC与△ADE成位似图形，位似中心为点A，若AD：AB=1：3，则△ADE与四边形DECB面积之比为（　　）

A. ：
B. ：
C. ：
D. ：

8. 如果反比例函数y＝的图象如图所示，那么二次函数y＝kx2－k2x－1的图象大致为（　）

A.
B.
C.
D.

二、填空题（本大题共6小题，共18分）

9. 将x-x2+x3分解因式的结果为______．
10. 观察下列方程：①x+=3；②x+=5；③x+=7，可以发现它们的解分别是①x=1或2；②x=2或3；③x=3或4．利用上述材料所反映出来的规律，可知关于x的方程x+=2n+4（n为正整数）的解x=______．
11. 如图，已知⊙O上三点A，B，C，半径OC=1，∠ABC=30°，切线PA交OC延长线于点P，则PA的长为______．
    
     

12. 若关于x的二次方程(m+1)x2-3x+2=0有两个相等的实数根，则m=            ．
13. 如图是反比例函数y=（x＞0）的图象，点C的坐标为（0，2），若点A是函数y=图象上一点，点B是x轴正半轴上一点，当△ABC是等腰直角三角形时，点B的坐标为______ ．
    
    
    
    
     

14. 已知△ABC，∠A=90°，AB=AC，直线l过直角顶点A，分别过点B、C向直线l作垂线，垂足分别为E、F，BE=7，CF=5，则EF=______．

三、解答题（本大题共10小题，共78分）

15. 计算：
16. 化简求值：÷（-a），其中a=-2．
17. 如图1，在△ABC中，AB=AC，AC平分∠BCD，连接BD，∠ABD=2∠CBD，∠BDC=∠ABD+∠ACD．
    （1）求∠A的度数；
    （2）如图2，连接AD，AE⊥AD交BC于E，连接DE，求证：∠DEC=∠BAE；
    （3）如图3，在（2）的条件下，点G为CE的中点，连接AG交BD于点F，若S△ABC=32，求线段AF的长．
    ​​​​​​​
18. 五星红旗作为中华民族五千年历史上第一面代表全体人民意志的民族之旗、团结之旗、胜利之旗、希望之旗、吉祥之旗，是中华人民共和国的标志和象征．某校九年级综合实践小组开展了测量学校五星红旗旗杆AB高度的活动．如图，他们在地面D处竖直放置标杆CD，并在地面上水平放置一个平面镜E，使得B，E，D在同一水平线上．该小组在标杆的F处通过平面镜E恰好观测到旗杆顶点A（此时∠AEB=∠FED），在F处分别测得旗杆顶点A的仰角为40°、平面镜E的俯角为45°，FD=1.6米，问旗杆AB的高度约为多少米？（结果保留整数）（参考数据：tan40°≈0.8，tan50°≈1.2，tan85°≈11）
19. 斑马线前“车让人”，不仅体现着对生命的尊重，也直接反映着城市的文明程度．如图，某路口的斑马线路段A-B-C横穿双向行驶车道，其中AB=BC=12米，在绿灯亮时，晓雯共用9秒通过AC，其中通过BC段的速度是通过AB段速度的2倍，求晓雯通过AB段时的速度．
20. 已知反比例函数y=的图象经过点（-2，3）．
    （1）求该反比例函数的表达式，并画出反比例函数的图象；
    （2）求一次函数y=-x+1与该反比例函数图象的交点坐标．
21. 2022年1月15日，广西龙江河发生严重的重金属镉污染事件．据专家介绍，重金属镉具有毒性，长期过量接触镉会引起慢性中毒，影响人体肾功能．为了解这次镉污染的程度，国务院派出的龙江河调查组抽取上层江水制成标本a1、a2，抽取中层江水制成标本b1、b2，抽取下层江水制成标本c1、c2．
    (1)若调查组从抽取的六个样本中送选两个样本到国家环境监测实验室进行检验，求刚好选送一个上层江水标本和一个下层江水标本的概率；
    (2)若每个样本的质量为500g，检测出镉的含量(单位：mg)分别为：0.3、0.2、0.7、0.5、0.3、0.4，请算出每500g河水样本中金属镉的平均含量；
    (3)据估计，受污染的龙江河河水共计2500万吨，请根据(2)的计算结果，估算出2500万吨河水中含镉量约为多少吨？
22. 如图，⊙O为△ABC的外接圆，直径AB=5．
    （1）用尺规作图，作出劣弧BC的中点D（保留作图痕迹，不写做法）；
    （2）连接AD，BD，若AC=3，求弦AD的长．
    
    
    
     

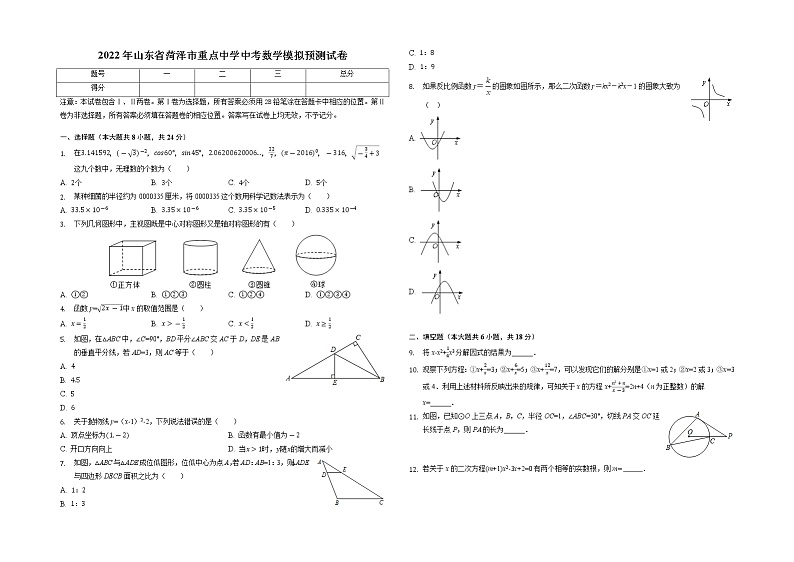
23. 如图①，在△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，且AD=AE．则CE=BD．现将△ADE绕点A顺时针方向旋转，旋转角为α（0°＜α＜180°）．如图②，连接CE，BD．
    （1）如图②，请直接写出CE与BD的数量关系．
    （2）将△ADE旋转至如图③所示位置时，请判断CE与BD的数量关系和位置关系，并加以证明．
    （3）在旋转的过程中，当△BCD的面积最大时，α=______．（直接写出答案即可）

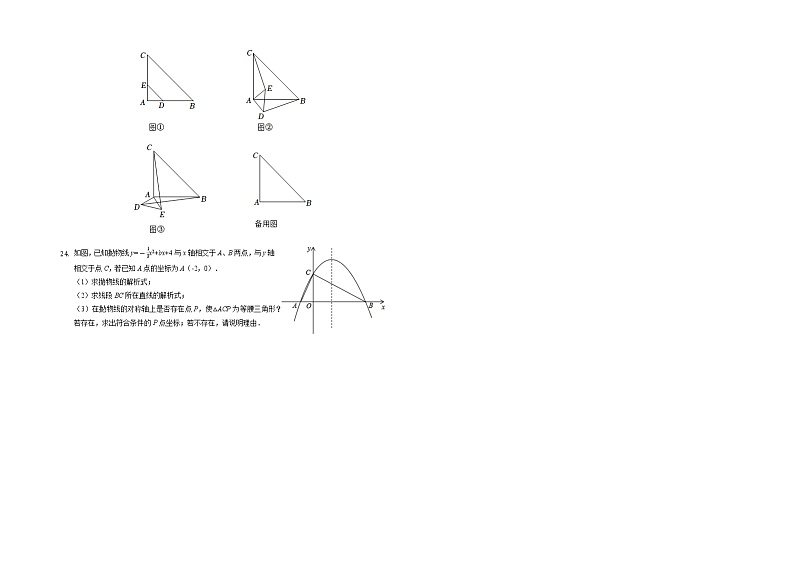
24. 如图，已知抛物线y=x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（-2，0）．
    （1）求抛物线的解析式；
    （2）求线段BC所在直线的解析式；
    （3）在抛物线的对称轴上是否存在点P，使△ACP为等腰三角形？若存在，求出符合条件的P点坐标；若不存在，请说明理由．
     

1.B

2.C

3.C

4.D

5.B

6.D

7.C

8.B

9.x

10.n+3或n+4

11.

12.

13.（4，0）或（，0）或（-1+，0）

14.12或2

15.解：原式=2（2-1）+3-2-1+4×
=4-2+3-2-1+2
=4．

16.解：原式=÷
=•
=，
当a=-2时，原式==．

17.（1）解：如图1中，设∠DBC=x．
∵AB=AC，∠ABD=2∠DBC，
∴∠ABD=2x，∠ABC=∠ACB=3x，
∵AC平分∠BCD，
∴∠ACD=∠ACB=3x，
∵∠D=∠ABD+∠ACD=5x，∠D+∠DBC+∠DCB=180°，
∴5x+x+6x=180°，
∴x=15°，
∴∠ABC=∠ACB=∠ACD=45°，∠ABD=30°，
∴∠A=180°-45°-45°=90°．
（2）证明：∵EA⊥DA，
∴∠EAD=∠A=90°，
∴∠BAE=∠CAD，
∵AB=AC，∠ABE=∠ACD=45°，
∴△ABE≌△ACD，
∴∠BAE=∠CAD，AE=AD，BE=CD，
∴∠AED=∠ADE=45°，
∵∠ACB=45°，
∴∠DEC=∠CAD，
∴∠DEC=∠BAE．
（3）解：如图3中，O是DE的中点，

∵S△ABC=•AB2=32，
∴AB=8或-8（舍弃），
由（1）、（2）及根据G是CE的中点可知：
AO=DE，GO=CD=BE，AO⊥DE，
所以有∠AOG=∠BED=90°+∠EOG=90°+∠EDC，
AO：DE=GO：BE=1：2，
∴△AOG∽△DEB，
∴∠GAO=∠BDE，
∴∠AFD=∠DOA=90°，
又∠ABF=30°，
∴AF=AB=4．

18.解：如图，过点F作FG⊥AB于G，则BG=DF，BD=FG．
设AB=x米，则BE=AB=x米，DE=DF=1.6米．
∴BD=DE+BE=FG=x+1.6，AG=x-1.6．
在直角△AGF中，∠AFG=40°，
∴tan40°=，即=tan40°≈0.8．
∴x=14.4≈14．
即：AB≈14米．
答：旗杆AB的高度约为14米．

19.解：设晓雯通过AB段时的速度为每秒x米，
根据题意，得：，
解得：x=2，
经检验：x=2 是原方程的解，且符合题意，
答：晓雯通过AB段时的速度为每秒2米．

20.解：（1）∵反比例函数y=的图象经过点（-2，3），
∴3=，解得k=-6，
∴反比例函数解析式为y=-．
图象如图所示：
；

（2）由题意可得，
解得，
故图象的交点坐标为（3，-2），（-2，3）．

21.解：(1)列表得：

∵一共有30种不同的结果，而一个上层江水样本和一个下层江水样本有8种情况，
∴ P(一个上层江水样本和一个下层江水样本)==；

(2)=×(0.3+0.2+0.7+0.5+0.3+0.4)=0.4(mg)；
答：每500 g河水样本中金属镉的平均含量为0.4mg；

(3)×2.5×107=20(t)．
答：2500万吨河水中含镉量约为20吨．

22.解：（1）如图所示，点D即为所求．

（2）连接OD，交BC于点E，连接AD，BD，

∵AC=3，AB=5，∠ACB=90°（直径所对的圆周角是直角），
∴BC=4（勾股定理），
又∵D是劣弧BC的中点，
∴OD垂直平分BC（垂径定理），
∴CE=BE=BC=2，
∴DE=OD-OE=-=1，BD=（勾股定理），
∴AD===．

23.135°

24.解：（1）将点A（-2，0）代入y=x2+bx+4中，
得，
解得：b=，
∴抛物线的解析式为y=x2+x+4；
（2）当x=0时，y=4，
∴点C的坐标为（0，4），
当y=0时，x2+x+4=0，
解得：x1=-2，x2=6，
∴点B的坐标为（6，0），
设直线BC的解析式为y=kx+n，
将点B （6，0），点C （0，4）代入解析式y=kx+n，得：
，
解得：，
∴直线BC的解析式为y=-x+4；
（3）∵抛物线y=x2+x+4与x轴相交于A（-2，0）、B（6，0）两点，
∴抛物线的对称轴为x=，
假设存在点P，设P（2，t），
则AC==，
AP==，
CP==，
∵△ACP为等腰三角形，
故可分三种情况：
①当AC=AP时，，
解得：t=±2，
∴点P的坐标为（2，2）或（2，-2）；
②当AC=CP时，，
解得：t=0或t=8，
∴点P的坐标为（2，0）或（2，8），
设直线AC的解析式为y=mx+n，
将点A（-2，0）、C（0，4）代入得，
解得：，
∴直线AC的解析式为y=2x+4，
当x=2时，y=4+4=8，
∴点（2，8）在直线AC上，
∴A、C、P在同一直线上，点（2，8）应舍去；
③当AP=CP时，，
解得：t=，
∴点P的坐标为（2，）；
综上可得，符合条件的点P存在，点P的坐标为：（2，2）或（2，-2）或（2，0）或（2，）．