2022年河南省周口市商水县中考数学仿真模拟试卷（含答案）

这是一份2022年河南省周口市商水县中考数学仿真模拟试卷（含答案），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年河南省周口市商水县中考数学仿真模拟试卷题号一二三总分得分    注意：本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题，所有答案必须填在答题卷的相应位置。答案写在试卷上均无效，不予记分。一、选择题（本大题共10小题，共30分）下列等式一定成立的是（　　）A.  B.  C.  D. 2022年3月25日，我国核电企业研发设计的具有完全自主知识产权的“华龙一号”示范工程全面建成投运，每年减少二氧化碳排放约1632万吨．用科学记数法表示1632万是（　　）A.  B.  C.  D. 长方体从正面看和从上面看所得到的图形如图所示，则这个长方体的体积是（　　）
A.  B.  C.  D. 下列式子一定成立的是（　　）A.  B.  C.  D. 下列调查中，调查方式选择合理的是（　　）A. 调查你所在班级同学的身高，采用抽样调查方式
B. 调查嘉陵江的水质情况，采用抽样调查的方式
C. 调查市场上某品牌电脑的使用寿命，采用普查的方式
D. 要了解全国初中学生的业余爱好，采用普查的方式如图，AB是半圆O的弦，DE是直径，过点B的切线BC与⊙O相切于点B，与DE的延长线交于点C，连接BD，若四边形OABC为平行四边形，则∠BDC的度数为（　　）
A.  B.  C.  D. 如图，一次函数y=kx+b（k＞0）的图象过点（-1，0），则不等式k（x-2）+b＞0的解集是（　　）A.
B.
C.
D. 为绿化、美化环境，某园林部门计划在某地修建一个面积为150平方米的矩形花园，它的长比宽多5米，设长为x米，可列方程为（　　）A.  B.
C.  D. 如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F，若∠BAC=112°，则∠EAF为（　　）
A.  B.  C.  D. 如图，平行四边形ABCD的周长为12，∠A=60°，设边AB的长为x，四边形ABCD的面积为y，则下列图象中，能表示y与x函数关系的图象大致是（　　）A. B. C. D.  二、填空题（本大题共5小题，共15分）（π-2017）0+（-1）2019=______．函数中，自变量的取值范围是__________.《易经》是中华民族聪明智慧的结晶．如图是《易经》中的一种卦图，每一卦由三根线组成（线形为“”或“”），如正北方向的卦为“”．从图中任选一卦，这一卦中恰有1根“”和2根“”的概率是______．
  直角三角形一条直角边长为8cm，它所对的角为30°，则斜边为______．等腰△ABC中，顶角∠A=40°，则一个底角∠B= ______ 度. 三、解答题（本大题共8小题，共75分）计算：
（1）；
（2）．为积极响应教育部“停课不停学”的号召，某中学组织本校优秀教师开展线上教学，经过近三个月的线上授课后，在五月初复学．该校为了解学生不同阶段学习效果，决定随机抽取八年级部分学生进行两次跟踪测评，第一次是复学初对线上教学质量测评，第二次是复学一个月后教学质量测评．根据第一次测试的数学成绩制成频数分布直方图（图1）．

复学一个月后，根据第二次测试的数学成绩得到如下统计表：成绩30≤x＜4040≤x＜5050≤x＜6060≤x＜7070≤x＜8080≤x＜9090≤x≤100人数133815m6根据以上图表信息，完成下列问题：
（1）m=______；
（2）请在图2中作出两次测试的数学成绩折线图，并对两次成绩作出对比分析（用一句话概述）；
（3）某同学第二次测试数学成绩为78分．这次测试中，分数高于78分的至少有______人，至多有______人；
（4）请估计复学一个月后该校800名八年级学生数学成绩优秀（80分及以上）的人数．如图，AB是一条笔直的长为500m的滑雪坡道，某运动员从坡顶A滑出，沿直线滑向坡底B，她的滑行距离y（单位：m）与滑行时间x（单位：s）的部分对应值如下表．x01234…y04.51428.548…（1）用所学过的函数知识猜想y是x的什么函数，并求出y与x之间的函数表达式；
（2）一架无人机在AB上空距地面292m的P处悬停，此时在A处测得无人机的仰角为53°．无人机和该运动员同时开始运动，无人机以6.3m/s的速度匀速水平飞行拍摄，离A处越来越远．已知无人机（看成一个点）与AB（看成一条线段）所确定的平面始终垂直于地面，AB与地面MN的夹角为26°．求该运动员滑行多久时，她恰在无人机的正下方．
（参考数据：tan53°≈，sin26°≈0.44，cos26°≈0.90，tan26°≈0.49．）
如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）如果⊙O的半径为5，cos∠DAB=，求BF的长．
  如图，一次函数y=kx+b（k≠0）的图象与反比例函数y=（m≠0）的图象交于A（1，2）、B（n，-1）两点.
（1）求m、n的值；
（2）根据图象，直接写出不等式kx+b＜的解集.



  某商店销售一种进价50元/件的商品，经市场调查发现：该商品的每天销售量y（件）是售价x（元/件）的一次函数，其售价、销售量的二组对应值如表：售价x（元/件）5565销售量y（件/天）9070（1）直接写出y关于售价x的函数关系式：______；
（2）若某天销售利润为800元，求该天的售价为多少元/件？
（3）设商店销售该商品每天获得的利润为W（元），求W与x之间的函数关系式，并求出当销售单价定为多少时，该商店销售这种商品每天获得的利润最大？抛物线C1：y1=-x2+2x的顶点为A，与x轴的正半轴交于点B.
（Ⅰ）求点A点B的坐标；
（Ⅱ）设直线y2=x+m，若无论x取何相同值时，都有y2＞y1，求m的范围；
（Ⅲ）将抛物线C1上的点（x，y）变为（kx，ky）（|k|＞1），变换后得到的抛物线记作C2，抛物线C2的顶点为C，点P在抛物线C2上，满足S△PBC=S△ABC，且∠ACP=90°.
①当k＞1时，求k的值；
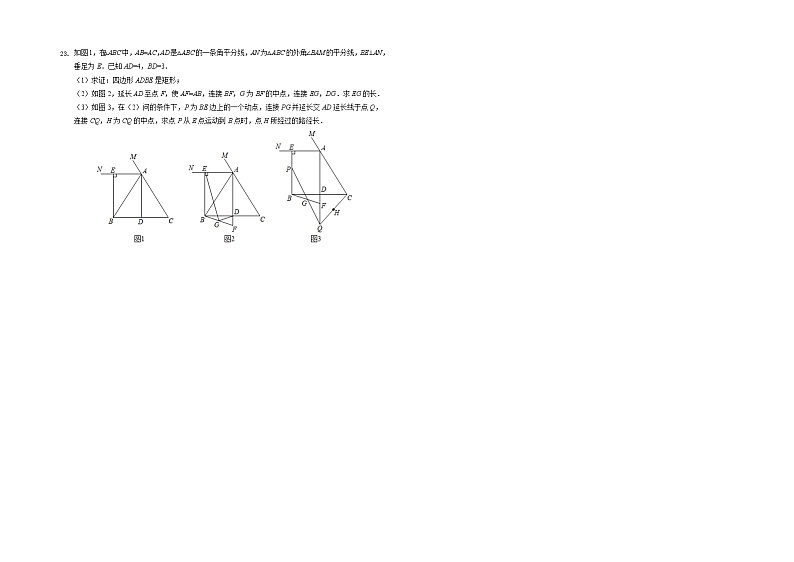
②当k＜-1时，请你直接写出k的值，不必说明理由.如图1，在△ABC中，AB=AC，AD是△ABC的一条角平分线，AN为△ABC的外角∠BAM的平分线，BE⊥AN，垂足为E．已知AD=4，BD=3．
（1）求证：四边形ADBE是矩形；
（2）如图2，延长AD至点F，使AF=AB，连接BF，G为BF的中点，连接EG，DG．求EG的长．
（3）如图3，在（2）问的条件下，P为BE边上的一个动点，连接PG并延长交AD延长线于点Q，连接CQ，H为CQ的中点，求点P从E点运动到B点时，点H所经过的路径长．

 1.B2.B3.A4.B5.B6.B7.D8.A9.D10.C11.012.x≥2.13.14.16cm15.7016.解：（1）
=+
=+
=3+；

（2）
=3-2+1-2+1
=3-2．17.解：（1）14；
（2）折线图如下图所示，

​​​​​​​复学后，学生的成绩总体上有了明显的提升；
（3）20，34；
​​​​​​​（4）800×=320（人），
答：复学一个月后该校800名八年级学生数学成绩优秀（80分及以上）的有320人．18.解：（1）猜想y与x是二次函数关系，
设y=ax2+bx，
把（1，4.5）（2，14）代入得：，
解得：，
∴y=2.5x2+2x，
当x=3时，y=2.5×9+6=28.5，
当x=4时，y=2.5×16+8=48，
∴y=2.5x2+2x符合题意，
∴y与x之间的函数表达式为：y=2.5x2+2x；
（2）设运动员滑行ts时，她恰在无人机的正下方，
此时运动员滑行了（2.5t2+2t）m，无人机飞行了6.3t m到达点P′，
过点P′作P′D⊥MN交AB于C，交MN于D，如图所示：
此时运动员滑行到点C，
∴BC=AB-AC=500-（2.5t2+2t），
过点A作AF⊥MN于F，过点A作AG⊥P′D于G，过点P作PE⊥AG于E，
则四边形AFDG与四边形PEGP′都是矩形，
∵AB=500m，∠ABF=26°，
∴AF=GD=AB×sin26°≈500×0.44=220（m），∠GAC=∠ABF=26°，
∵无人机在AB上空距地面292m的P处悬停，
∴PE=P′G=292-AF=292-220=72（m），
在Rt△AGC中，AG=AC×cos26°≈（2.5t2+2t）×0.9=2.25t2+1.8t，
∴AE=AG-EG=2.25t2+1.8t-6.3t=2.25t2-4.5t，
在Rt△APE中，tan53°=≈，
∴3×72=4×（2.25t2-4.5t），
解得：t1=6，t2=-4（不合题意舍去），
∴该运动员滑行6s时，她恰在无人机的正下方．19.（1）证明：连接OD，如图，
∵AB为⊙0的直径，
∴∠ADB=90°，
∴AD⊥BC，
∵AB=AC，
∴AD平分BC，即DB=DC，
∵OA=OB，
∴OD为△ABC的中位线，
∴OD∥AC，
∵DE⊥AC，
∴OD⊥DE，
∴EF是⊙O的切线；

（2）∵∠DAC=∠DAB，
∴∠ADE=∠ABD，
在Rt△ADB中，sin∠ADE=sin∠ABD=cos∠DAB==，而AB=10，
∴AD=8，
在Rt△ADE中，sin∠ADE==，
∴AE=，
∵OD∥AE，
∴△FDO∽△FEA，
∴=，即=，
∴BF=．20.解：（1）∵A（1，2）在反比例函数y=（m≠0）的图象上，
∴m=1×2=2，
∴反比例函数的表达式为y=，
∵点B（n，-1）也在反比例函数y=的图象上，
∴-1=，
∴n=-2；
（2）如图所示，当kx+b＜时，x的取值范围是x＜-2或0＜x＜1，
所以不等式kx+b＜的解集为x＜-2或0＜x＜1．21.y=-2x+20022.解：（Ⅰ）∵y1=-x2+2x=-（x-1）2+，
∴A（1，），
当y1=0时，即-x2+2x=0，
∴x1=0，x2=2，
∴B（2，0）；
（Ⅱ）∵y1=-x2+2x开口向下，顶点坐标为A（1，），
∵无论x取何相同值时，都有y2＞y1，
∴直线y2=x+m与抛物线y1=-x2+2x无交点，
即x+m=-x2+2x无实数根，
∴△=（）2-4m＜0，
∴m＞，
∴m的范围是m＞．
（Ⅲ）①如图1中，当k＞1时，
∵抛物线C2经过原点O，（k，k），（2k，0）三点，
∴抛物线C2的解析式为y=-x2+2x，
∴O、A、C三点共线，且顶点C为（k，k），

如图，∵S△PBC=S△ABC，
∴BP∥AC，
过点P作PD⊥x轴于D，过点B作BE⊥AO于E，
由题意知△ABO是边长为2的正三角形，四边形CEBP是矩形，
∴OE=1，CE=BP=2k-1，
∵∠PBD=60°，
∴BD=k-，PD=（2k-1），
∴P（k+，（2k-1）），
∴（2k-1）=-（k+）2+2（k+），
解得：k=；
②如图2中，当k＜-1时，

∵抛物线C2经过原点O，（k，k），（2k，0）三点，
∴抛物线C2的解析式为y=-x2+2x，
∴O、A、C′三点共线，且顶点C′为（k，k），
作△ABO关于y轴对称的△A′B′O，OE′⊥A′B′，
∵S△PAC′=S△ABC=S△AC′B′，
∴A′P∥AC′，由题意四边形PC′OE′是矩形，
∴PE′=OC′=-2k，B′E′=1，PB′=-2k-1，
在Rt△PDB′中，∵∠PDB′=90°，∠PB′D=∠A′B′O=60°，
∴DB′=PB′=，DP=（-2k-1），
∴点P坐标[，（2k+1）]，
∴（2k+1）=-（）2+2（）
∴k=-．23.证明：（1）∵AB=AC，AD是△ABC的一条角平分线，
∴BD=CD，AD⊥BC，∠ABC=∠ACB，
∴∠BAM=∠ABC+∠ACB=2∠ABC，
∵AN平分∠BAM，
∴∠MAN=∠BAN=∠BAM，
∴∠BAN=∠ABC，
∴AN∥BC，
∴∠DAE+∠ADB=180°，
∴∠DAE=90°，
又∵BE⊥AN，AD⊥BC，
∴∠AEB=∠ADB=∠DAE=90°，
∴四边形ADBE是矩形；
（2）如图2，延长AF，EG交于点K，

在矩形ADBE中，AD=4，BD=3，
∴BE=AD=4，AE=BD=3，BE∥AD，∠ADB=∠DAE=90°，
∴AB==5，
∴AF=AB=5，
∵BE∥AD，
∴∠BEG=∠K，∠EBG=∠KFG，
∵G为BF的中点，
∴BG=GF，
∴△BEG≌△FKG（AAS），
∴BE=FK=4，EG=GK，
∴AK=9，
∴EK==3，
∴EG=；
（3）如图3，取AC的中点J，连接CF，JH，

∵点J是AC的中点，点H是CQ的中点，
∴JH是△ACQ的中位线，
∴JH=，JH∥AQ，
∴点H在JH上移动，
当点P在点E时，由（2）可知AQ=9，
当点P在点B时，AQ=AF=5，
∴点H经过的路径长为（9-5）=2．