2022年江苏省南通市中考数学考前模拟预测试卷 (word版含答案)

这是一份2022年江苏省南通市中考数学考前模拟预测试卷 (word版含答案)，共21页。

2022年江苏南通中考数学考前模拟预测试卷
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）计算﹣1﹣2＝（　　）
A．﹣1 B．1 C．﹣3 D．3
2．（3分）根据“数据安徽”APP发布的最新数据，2019年上半年安庆市财政总收入182.9亿元，增速9.19%，在全省各市排名中上升一位，排名第五位，将182.9亿用科学记数法表示为（　　）
A．1.829×109 B．1.829×1010 C．1.829×1011 D．1.829×1012
3．（3分）下列计算正确的是（　　）
A．3a2+a2＝4a4 B．a2•a3＝a6
C．2a2+3a3＝5a5 D．（a2）3＝a6
4．（3分）在下列调查中，适宜采用普查的是（　　）
A．了解我校八（1）班学生校服的尺码情况
B．检测一批电灯泡的使用寿命
C．调查江苏卫视《最强大脑》栏目的收视率
D．了解全国中学生的视力情况
5．（3分）如图是一个几何体的三视图，则该几何体可能是下列的（　　）

A． B． C． D．
6．（3分）如图，在菱形ABCD中，对角线AC、BD交于点O，且AC＝6，BD＝8，过A点作AE垂直BC，交BC于点E，则BECE的值为（　　）

A．512 B．725 C．718 D．524
7．（3分）在一次爱心捐助活动中，八年级（1）班40名同学共捐款275元，已知同学们捐款的面额只有5元、10元两种，求捐5元和10元的同学各有多少名？若设捐5元的同学有x名，捐10元的有y名，则可列方程组为（　　）
A．x-y=405x+10y=275 B．x-y=4010x+5y=275
C．x+y=405x+10y=275 D．x+y=4010x+5y=275
8．（3分）已知关于x的不等式组x-a＞03-2x＞0的整数解共有5个，则a的取值范围是（　　）
A．﹣4＜a＜﹣3 B．﹣4≤a＜﹣3 C．a＜﹣3 D．﹣4＜a＜32
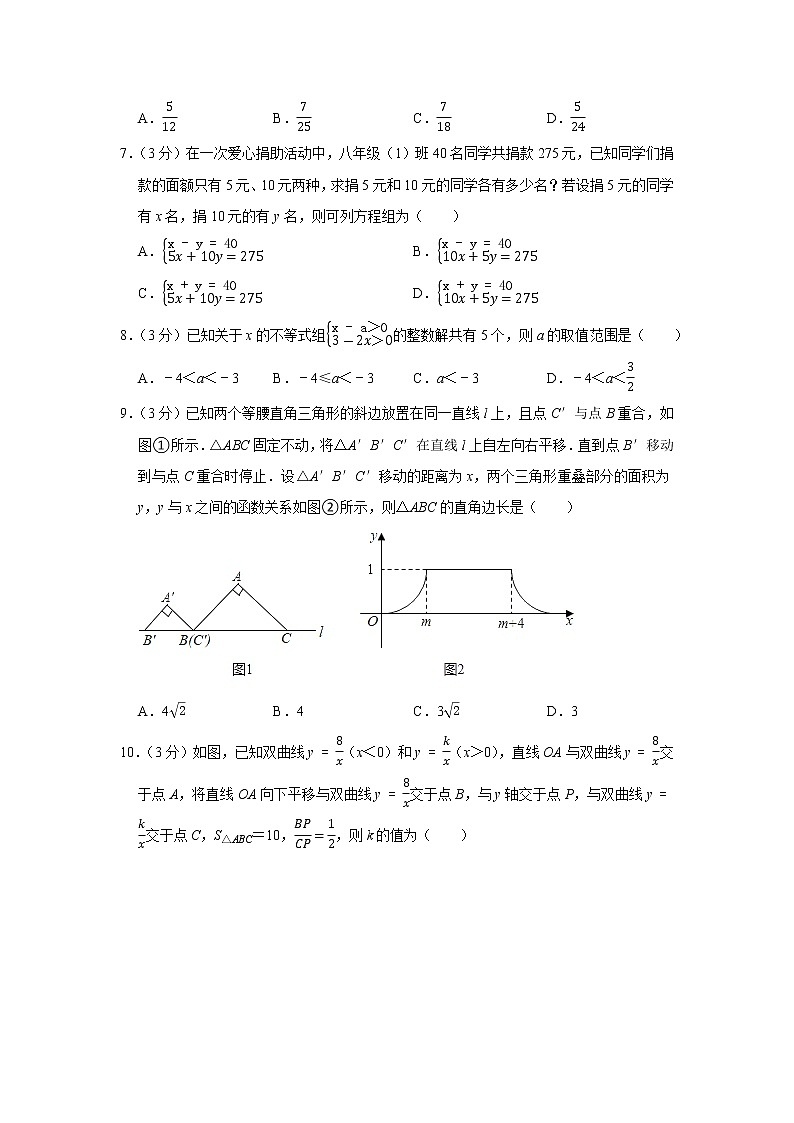
9．（3分）已知两个等腰直角三角形的斜边放置在同一直线l上，且点C′与点B重合，如图①所示．△ABC固定不动，将△A′B′C′在直线l上自左向右平移．直到点B′移动到与点C重合时停止．设△A′B′C′移动的距离为x，两个三角形重叠部分的面积为y，y与x之间的函数关系如图②所示，则△ABC的直角边长是（　　）

A．42 B．4 C．32 D．3
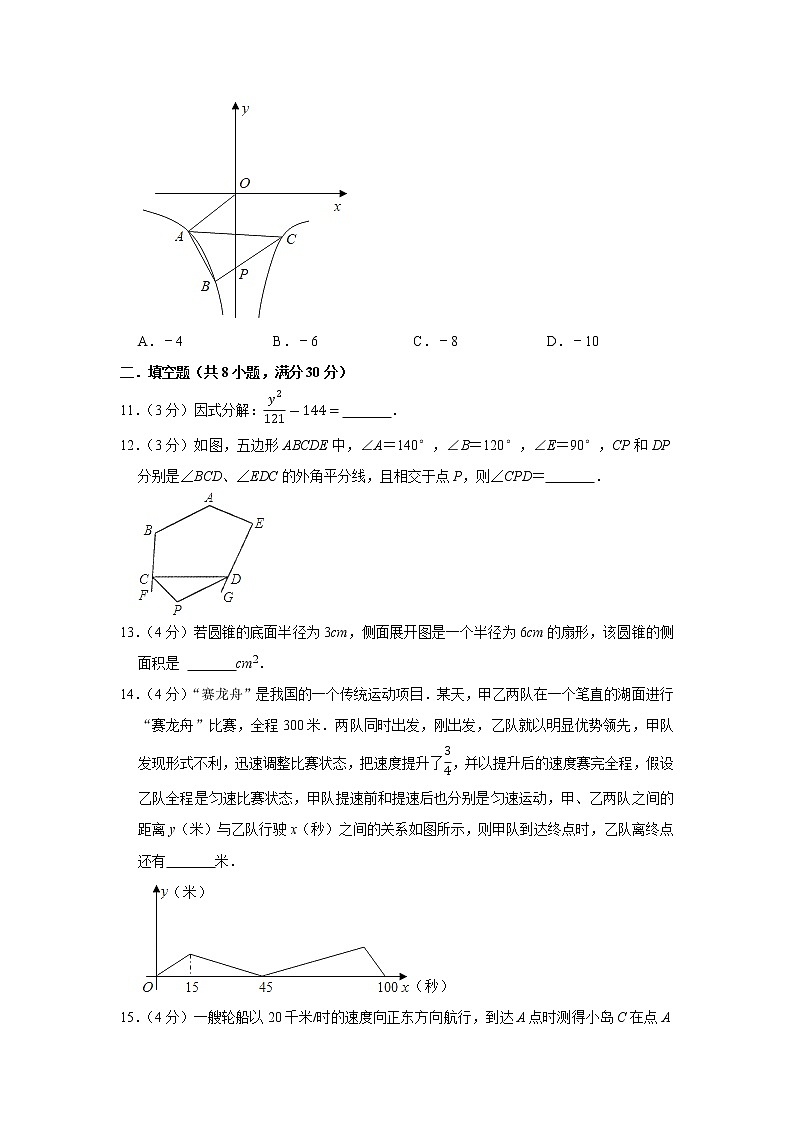
10．（3分）如图，已知双曲线y=8x（x＜0）和y=kx（x＞0），直线OA与双曲线y=8x交于点A，将直线OA向下平移与双曲线y=8x交于点B，与y轴交于点P，与双曲线y=kx交于点C，S△ABC＝10，BPCP=12，则k的值为（　　）

A．﹣4 B．﹣6 C．﹣8 D．﹣10
二．填空题（共8小题，满分30分）
11．（3分）因式分解：y2121-144=　 　．
12．（3分）如图，五边形ABCDE中，∠A＝140°，∠B＝120°，∠E＝90°，CP和DP分别是∠BCD、∠EDC的外角平分线，且相交于点P，则∠CPD＝　 　．

13．（4分）若圆锥的底面半径为3cm，侧面展开图是一个半径为6cm的扇形，该圆锥的侧面积是 　 　cm2．
14．（4分）“赛龙舟”是我国的一个传统运动项目．某天，甲乙两队在一个笔直的湖面进行“赛龙舟”比赛，全程300米．两队同时出发，刚出发，乙队就以明显优势领先，甲队发现形式不利，迅速调整比赛状态，把速度提升了34，并以提升后的速度赛完全程，假设乙队全程是匀速比赛状态，甲队提速前和提速后也分别是匀速运动，甲、乙两队之间的距离y（米）与乙队行驶x（秒）之间的关系如图所示，则甲队到达终点时，乙队离终点还有　 　米．

15．（4分）一艘轮船以20千米/时的速度向正东方向航行，到达A点时测得小岛C在点A北偏东60°方向：继续航行半小时到达B点，这时测得小岛C在点B的东北方向；再继续航行　 　小时，轮船刚好到达小岛C的正南方向（3≈1.732，2≈1.414）．
16．（4分）已知x1，x2 的是一元二次方程3x2﹣2x﹣5＝0 的两个实数根，则x1+x2＝　 　．
17．（4分）定义：对于平面直角坐标系xOy中的线段PQ和点M，在△MPQ中，当PQ边上的高为2时，称M为PQ的“等高点”，称此时MP+MQ为PQ的“等高距离”．
（1）若点P的坐标为（1，2），点Q的坐标为（4，2），则在点A（1，0），B（52，4），C（0，3）中，PQ的“等高点”是点　 　；
（2）若P（0，0），PQ＝2，当PQ的“等高点”在y轴正半轴上且“等高距离”最小时，点Q的坐标是　 　．
18．（4分）等腰直角三角形中，斜边长为1，则直角边长为　 　．
三．解答题（共8小题，满分90分）
19．（10分）（1）2x-1=1x-2；
（2）化简求值：（a﹣1）2﹣a（a+1），其中a=16．
20．（11分）在沙滩上撑开的太阳伞如图所示，伞檐离地面的距离是4m，伞面撑开最宽处有2m，伞形成的阴影离伞脚1m，试问身高1.6m的小明在什么范围内不会被太阳光晒到？

21．（12分）某中学开展歌咏比赛，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，复赛成绩（满分为100分）如图所示．
（1）根据图示填写下表：
班级
平均数（分）
中位数（分）
众数（分）
九（1）
　 　
85
　 　
九（2）
85
　 　
100
（2）已知九年级（2）班复赛成绩的方差为160，计算九年级（1）班复赛成绩的方差，并分析哪个班的复赛成绩稳定．

22．（10分）一个不透明的口袋中装有2个红球、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．
（1）从口袋中任意摸出1个球，恰好摸到红球的概率是　 　；
（2）先从口袋中随机摸出一个球，不放回，再从中口袋中随机摸出一个球．请用列举法（画树状图或列表）求摸出一个红球和一个白球的概率．
23．（9分）如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
（1）求证：BE＝EC．
（2）填空：若∠B＝30°，DE=3，则弧DC的长度为 　 　．

24．（12分）某学校欲购置一批标价为4800元的某种型号电脑，需求数量在6至15台之间．经与两个专卖店商谈，优惠方法如下：
甲店：购买电脑打八折；
乙店：先赠一台电脑，其余电脑打九折优惠．
设学校欲购置x台电脑，甲店购买费用为y甲（元），乙店购买费用为y乙（元）．
（1）分别写出购买费用y甲、y乙与所购电脑x（台）之间的函数关系式；
（2）对x的取值情况进行分析，说明这所学校购买哪家电脑更合算？
25．（13分）矩形纸片ABCD中，AB＝4．
实践思考：
（1）连接BD，将纸片折叠，使点B落在边AD上，对应点为E，折痕为GH，点G，H分别在AB，BD上．若AD=3AB，如图①．
①BD＝　 　，tan∠ADB＝　 　；
②若折叠后的△AGE为等腰三角形，则△DHE为　 　三角形；
③隐去点E，G，H，线段GE，EH，折痕GH，如图②，过点D作DF⊥BD交BC的延长线于点F，连接AF，AC，则S△ACF＝　 　；
（2）若AD＝（2+1）AB，如图③，点M在AD边上，且AM＝AB，连接BM，求∠DBM的度数；
拓展探究：
（3）若AD=2AB，如图④，N为边AD的中点，P为矩形ABCD内一点，连接BP，CP，满足∠BPC＝90°，Q是边AB上一动点，则PQ+QN的最小值为　 　．

26．（13分）定义：如果二次函数y＝a1x2+b1x+c1（a1≠0，a1、b1、c1是常数）与y＝a2x2+b2x+c2（a2≠0，a2、b2、c2是常数）满足a1+a2＝0，b1＝b2，c1+c2＝0，则这两个函数互为“旋转函数”．请解决下列问题：
（1）求出二次函数y＝x2﹣2x+1的旋转函数的顶点坐标；
（2）若二次函数y1＝x2+（m+8n）x+16与y2＝﹣x2﹣6x+2n﹣7m互为“旋转函数”，直线l与函数y1，y2的图象都只有一个公共点，求（m+n）2020的值以及直线l的解析式；
（3）在平面直角坐标系中，坐标原点为O，已知点P（2，0），⊙p与y轴相切，交x轴正半轴于点A，点B在⊙p上，且∠BAO＝30°，△A′OB'与△AOB关于原点对称，若两个二次函数的图象分别经过A′、O、B′与A、O、B三点，求证：这两个二次函数互为“旋转函数”．

参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．【解答】解：﹣1﹣2＝﹣1+（﹣2）＝﹣3，
故选：C．
2．【解答】解：将182.9亿用科学记数法表示为182.9×108＝1.829×1010．
故选：B．
3．【解答】解：A，3a2+a2＝4a2，故此选项不符合题意；
B，a2•a3＝a2+3＝a5，故此选项不符合题意；
C，2a2+3a3≠5a5，故此选项不符合题意；
D，（a2）3＝a2×3＝a6，故此选项符合题意；
故选：D．
4．【解答】解：A．了解我校八（1）班学生校服的尺码情况，宜采取全面调查，因此选项A符合题意；
B．检测一批电灯泡的使用寿命，宜采取抽样调查，因此选项B不符合题意；
C．调查江苏卫视《最强大脑》栏目的收视率，宜采取抽样调查，因此选项C不符合题意；
D．了解全国中学生的视力情况，宜采取抽样调查，因此选项D不符合题意；
故选：A．
5．【解答】解：观察三视图发现，该几何体是正方体右上方去掉一个角，
故选：A．
6．【解答】解：∵四边形ABCD是菱形，
∴CO=12AC＝3，BO=12BD＝4，AO⊥BO，
∴BC=CO2+BO2=32+42=5，
∵S菱形ABCD=12AC•BD＝BC×AE，
∴AE=12×6×85=245．
在Rt△ABE中，BE=AB2-AE2=52-(245)2=75，
∴CE＝BC﹣BE＝5-75=185，
∴BECE的值为718，
故选：C．

7．【解答】解：∵八年级（1）班共有40名同学，
∴x+y＝40；
又∵八年级（1）班共捐款275元，
∴5x+10y＝275．
∴所列方程组为x+y=405x+10y=275．
故选：C．
8．【解答】解：解不等式x﹣a＞0，得：x＞a，
解不等式3﹣2x＞0，得：x＜1.5，
∵不等式组的整数解有5个，
∴﹣4≤a＜﹣3．
故选：B．
9．【解答】解：函数图象可知，当x＝m时，点B'到达点B，如图①，
当x＝m+4时，点C'到达点C，如图②，
∴B'C'＝m，BC＝m+4，
∴A'B'＝A'C'=22B'C'=22m，AB=22BC，
由函数图象可知当m＜x＜m+4时，重合部分的面积为1，
∴S△A'B'C'=12A'B'⋅A'C'=12⋅22m⋅22m=1，
∴m＝2，
∴BC＝2+4＝6，
∴AB=22×6＝32，
∴△ABC的直角边长度为32，
故选：C．

10．【解答】解：如图连接OB，OC，作BE⊥OP于E，CF⊥y轴于F．

∵OA∥BC，
∴S△OBC＝S△ABC＝10，
∵BPCP=12，
∴S△OPB=103，S△OPC=203，
∵S△OBE=12×8=4，
∴S△PBE=23，
∵△BEP∽△CFP，
∴S△CFP=23×4=83，
∴S△OCF=203-83=4，
∴k＝﹣8．
故选：C．
二．填空题（共8小题，满分30分）
11．【解答】解：y2121-144=（y11+12）（y11-12）．
故答案为：（y11+12）（y11-12）．
12．【解答】解：多边形的内角和定理：（n﹣2）•180°＝540°，
∴∠BCD+∠EDC＝540°﹣140°﹣120°﹣90°＝190°，
又∵CP和DP分别是∠BCD、∠EDC的外角平分线，
∴∠PCD+∠PDC=12（360°﹣∠BCD﹣∠EDC）＝85°，
根据三角形内角和定理得：∠CPD＝180°﹣85°＝95°．
故答案为：95°．
13．【解答】解：由题意得：圆锥的侧面积＝πrl＝π×3×6＝18π（cm2）．
故答案为：18π．
14．【解答】解：由图可得，
乙队的速度为300÷100＝3（米/秒），
设甲队开始的速度为a米/秒，
15（3﹣a）＝（45﹣15）×[a（1+34）﹣3]，
解得a＝2，
∴甲队提速后的速度为2×（1+34）＝3.5（米/秒），
∴甲队到达终点用的时间为：15+（300﹣15×2）÷3.5＝15+5407=15+7717=9217（秒），
∴甲队到达终点时，乙队离终点还有3×（100﹣9217）＝3×767=3×557=1657（米），
故答案为：1657．
15．【解答】解：如图，过C作CD⊥BC交BC的延长线于D，
由题意得：AB＝20×12=10（千米），∠BAC＝90°﹣60°＝30°，∠CBD＝45°，
∴AD=3CD，△BDC是等腰直角三角形，
∴BD＝CD，
设BD＝CD＝x千米，则AD=3x千米，
∵AD﹣BD＝AB，
∴3x﹣x＝10，
解得：x＝53+5，
∴BD＝（53+5）千米，
∴53+520=3+14（小时），
即再继续航行3+14小时，轮船刚好到达小岛C的正南方向，
故答案为：3+14．

16．【解答】解：根据根与系数的关系得x1+x2=--23=23．
故答案为：23．
17．【解答】解：（1）①∵P（1，2），Q（4，2），
∴在点A（1，0），B（ 52，4）到PQ的距离为2．
∴PQ的“等高点”是A或B，
故答案为：A或B；
（2）如图2，过PQ的“等高点”M作MN⊥PQ于点N，

∴PQ＝2，MN＝2．
设PN＝x，则NQ＝2﹣x，
在Rt△MNP和Rt△MNQ中，由勾股定理得：
MP2＝22+x2＝4+x2，MQ2＝22+（2﹣x）2＝x2﹣4x+8，
∴MP2+MQ2＝2x2﹣4x+12＝2（x﹣1）2+10，
∵MP2+MQ2≤（MP+MQ）2，
∴当MP2+MQ2最小时MP+MQ也最小，此时x＝1，
即PN＝NQ，
∴△MPQ为等腰三角形，
∴MP＝MQ=22+12=5，
如图3，设Q坐标为（x，y），过点Q作QE⊥y轴于点E，

则在Rt△MNP和Rt△MNQ中由勾股定理得：
QE2＝QP2﹣OE2＝22﹣y2＝4﹣y2，QE2＝QM2﹣ME2＝（5）2﹣（5-y）2＝25y﹣y2，
∴4﹣y2＝25y﹣y2，
解得y=255，
QE2＝4﹣y2＝4﹣（255）2=165，
当点Q在第一象限时x=455，当点Q在第二象限时x=-455，
∴Q（455，255）或Q（-455，255），
故答案为：Q（455，255）或Q（-455，255）．
18．【解答】解：设等腰直角三角形的直角边长为a（a＞0），
则a2+a2＝12，
解得：a=22．
故答案是：22．
三．解答题（共8小题，满分90分）
19．【解答】解：（1）去分母得：2（x﹣2）＝x﹣1，
解得：x＝3，
经检验x＝3是分式方程的解；
（2）（a﹣1）2﹣a（a+1）
＝a2﹣2a+1﹣a2﹣a
＝﹣3a+1，
当a=16时，
原式＝﹣3×16+1=12．
20．【解答】解：如图，过太阳伞的一个端点E作EF⊥AD于F，设小明站在MN处时，其影子的最外端与点H重合，

∵NH∥EG，
∴∠NHM＝∠EGF，
又∵∠EFG＝∠NMH＝90°，
∴△EFG∽△NMH，
∴EFNM=FGMH，
∴41.6=2MH，
∴MH＝0.8，
∴AM＝3﹣0.8＝2.2（m），
∴小明站在伞脚的右侧，离伞脚1m到2.2m处，不会被太阳光晒到．
21．【解答】解：（1）九年级（1）班的平均数=75+80+85+85+1005=85（分），九（1）班的众数为85，
九年级（2）班5名选手的复赛成绩为：70，75，80，100，100，
∴九年级（2）班5名选手的复赛成绩的中位数为80；
故答案为：85，85，80；
（2）S12=15×[（75﹣85）2+（80﹣85）2+（85﹣85）2+（85﹣85）2+（100﹣85）2]＝70，
S22＝160，
因为S12＜S22，
所以九（1）班的复赛成绩稳定．
22．【解答】解：（1）∵4个小球中有2个红球，
∴任意摸出1个球，恰好摸到红球的概率是24=12，
故答案为：12；
（2）列表如下：

红
红
白
黑
红
﹣﹣﹣
（红，红）
（白，红）
（黑，红）
红
（红，红）
﹣﹣﹣
（白，红）
（黑，红）
白
（红，白）
（红，白）
﹣﹣﹣
（黑，白）
黑
（红，黑）
（红，黑）
（白，黑）
﹣﹣﹣
所有等可能的情况有12种，其中摸出一个红球和一个白球的有4种可能，
∴摸出一个红球和一个白球的概率为412=13．
23．【解答】（1）证明：连接DO．
∵∠ACB＝90°，AC为直径，
∴EC为⊙O的切线；
又∵ED也为⊙O的切线，
∴EC＝ED，
又∵∠EDO＝90°，
∴∠BDE+∠ADO＝90°，
∵OD＝OA，
∴∠A＝∠ADO，
∴∠BDE+∠A＝90°
又∵∠B+∠A＝90°，
∴∠BDE＝∠B，
∴BE＝ED，
∴BE＝EC；

（2）解：∵DE=3，BE＝ED，BE＝EC；
∴BC＝23，
∵∠ACB＝90°，∠B＝30°，
∴AC＝2，∠A＝60°，
∵AC为直径，
∴OC＝1，
∵∠A＝60°，
∴∠DOC＝2A＝120°，
∴弧DC的长度为120π×1180=2π3．
故答案为：2π3．

24．【解答】解：（1）由题意可得，y甲＝4800×0.8x＝3840x（6≤x≤15）；
y乙＝4800×0.9（x﹣1）＝4320x﹣4320（6≤x≤15）；
（2）当3840x＝4320x﹣4320时，解得x＝9，即当购买9台电脑时，到两家商店购买费用相同；
当3840x＜4320x﹣4320时，解得x＞9，即当10≤x≤15时，到甲商店更合算；
当3840x＞4320x﹣4320时，解得x＜9，即当6≤x≤8时，到乙商店更合算．
25．【解答】解：（1）①∵四边形ABCD是矩形，
∴∠A＝90°，
∵AB＝4，AD=3AB，
∴AD=3AB＝43，
∴BD=AB2+AD2=42+(43)2=8，
tan∠ADB=ABAD=443=33，
故答案为：8，33；
②由①得：tan∠ADB=33，
∴∠ADB＝30°，
∴∠ABD＝90°﹣∠ADB＝60°，
∵∠A＝90°，△AGE为等腰三角形，
∴∠AEG＝45°，
由折叠的性质得：∠GEH＝∠ABD＝60°，
∴∠DEH＝180°﹣∠AEG﹣∠GEH＝180°﹣45°﹣60°＝75°，
∴∠DHE＝180°﹣∠DEH﹣∠ADB＝180°﹣75°﹣30°＝75°，
∴∠DEH＝∠DHE，
∴DE＝DH，
∴△DHE是等腰三角形，
故答案为：等腰；
③∵四边形ABCD是矩形，
∴∠ABC＝∠BCD＝∠ADC＝90°，CD＝AB＝4，
∴∠DCF＝90°，
由②得：∠ADB＝30°，
∴∠BDC＝90°﹣∠ADB＝60°，
∵DF⊥BD，
∴∠BDF＝90°，
∴∠CDF＝90°﹣∠BDC＝30°，
∴CF=33CD=433，
∴S△ACF=12CF×AB=12×433×4=833，
故答案为：833；
（2）∵∠A＝90°，AM＝AB，
∴△ABM是等腰直角三角形，
∴∠AMB＝45°，AM＝AB＝4，BM=2AB＝42，
∵AD＝（2+1）AB＝42+4，
∴DM＝AD﹣AM＝42，
∴BM＝DM，
∴∠DBM＝∠BDM=12∠AMB＝22.5°；
（3）∵AD=2AB＝42，N为边AD的中点，
∴AN=12AD＝22，
作点N关于AB的对称点N'，
则AN'＝AN＝22，
∵∠BPC＝90°，
∴点P在以BC为直径的半圆O上，连接ON'交AB于Q，交半圆O于P，
则OP＝OB=12BC＝22，QN＝QN'，
此时PQ+QN的值最小＝PQ+QN'＝PN'，
∵∠N'AQ＝90°＝∠OBQ，∠AQN'＝∠BQO，AN'＝BO＝22，
∴△AQN'≌△BQO（AAS），
∴QN'＝QO，AQ＝BQ=12AB＝2，
∴QN'＝QO=BQ2+OB2=22+(22)2=23，
∴PQ+QN＝PN'＝2QO﹣OP＝43-22，
即PQ+QN的最小值为43-22，
故答案为：43-22．

26．【解答】解：（1）由二次函数y＝x2﹣2x+1可知，a1＝1，b1＝﹣2，c1＝1，
∵a1+a2＝0，b1＝b2，c1+c2＝0，
∴a2＝﹣1，b2＝﹣2，c2＝﹣1，
∴函数y＝x2﹣2x+1的“旋转函数”为y＝﹣x2﹣2x﹣1；
∴顶点坐标为（﹣1，0）；
（2）∵y1＝x2+（m+8n）x+16与y2＝﹣x2﹣6x+2n﹣7m互为“旋转函数”，
∴m+8n=-62n-7m=-16，
解得：m=2n=-1，
∴（m+n）2020＝（2﹣1）2020＝1，
∴y1＝x2﹣6x+16，y2＝﹣x2﹣6x﹣16；
设直线l的解析式为y＝kx+b，
则x2﹣6x+16＝kx+b与﹣x2﹣6x﹣16＝kx+b都有两个相等的实数根，
∴k1=2b1=0，k2=-14b2=0，
∴直线l的解析式为y＝2x或y＝﹣14x；
（3）证明：由题意得：点A的坐标为（4，0），点O的坐标为（0，0），
∴点B的坐标为（1，3）或（1，-3），
∵点A，B关于原点的对称点分别是A′，B′，
∴A′（﹣4，0），B′（﹣1，-3）或（﹣1，3），
∴可求得过点A，B，O的函数解析式为y1=-33x2+433x或y1=33x2-433x，
过点A′，B′，O的二次函数解析式为y2=33x2+433x或y2=-33x2-433x，
∴a1=-33，b1=433，c1＝0，a2=33，b2=433，c2＝0，
或者a1=33，b1=-433，c1＝0，a2=-33，b2=-433，c2＝0，
∴a1+a2＝0，b1＝b2，c1+c2＝0，
∴经过A′，O，B′与A，O，B三点的两个二次函数互为“旋转函数”．