2022年江苏省苏州市中考数学考前模拟预测试题（含答案）

这是一份2022年江苏省苏州市中考数学考前模拟预测试题（含答案），共22页。试卷主要包含了万亿元等内容，欢迎下载使用。

2022年苏州市中考数学考前模拟预测试题
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）若x＜0，则化简-x3y的结果是（　　）
A．﹣xxy B．x-xy C．﹣x-xy D．xxy
2．（3分）如图所示，正三棱柱的俯视图是（　　）

A． B． C． D．
3．（3分）如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列结论一定正确的是（　　）

A．AC＝AD B．AB⊥EB C．BC＝DE D．∠A＝∠EBC
4．（3分）如果m﹣n＝1，那么代数式(1-2nm+n)⋅m+nm2-2mn+n2的值为（　　）
A．﹣3 B．﹣1 C．1 D．3
5．（3分）下表是某报纸公布的我国“九五”期间国内生产总值（GDP）的统计表，那么这几年我国国内生产总值平均比上一年增长（　　）万亿元．
年份
1996
1997
1998
1999
2000
国内生产总值（万亿元）
6.6
7.3
7.9
8.2
8.9
A．0.46 B．0.575 C．7.78 D．9.725
6．（3分）下列坐标平面内的点，在直线y＝﹣x+3上的是（　　）
A．（﹣1，2） B．（﹣1，﹣2） C．（1，2） D．（1，﹣2）
7．（3分）足球比赛中，每场比赛都要分出胜负每队胜1场得3分，负一场扣1分，某队在8场比赛中得到12分，若设该队胜的场数为x负的场数为y，则可列方程组为（　　）
A．x+y=83x-y=12 B．x-y=83x-y=12
C．x+y=183x+y=12 D．x-y=83x+y=12
8．（3分）如图，抛物线y1=12(x-3)2+1与y2＝a（x+3）2﹣1交于点A，分别交y轴于点P，Q，过点A作x轴的平行线，分别交两条抛物线于点B，C．已知B（5，3），则以下结论：
①两抛物线的顶点关于原点对称；
②A（2，3）；
③C（﹣7，3）；
④PQ＝2．
其中正确结论是（　　）

A．①② B．①③ C．③④ D．②④
9．（3分）如图，在平行四边形ABCD中，∠ABC＝45°，E、F分别在CD和BC的延长线上，AE∥BD，∠EFC＝30°，AB＝1．则CF的长为（　　）

A．2+6 B．22 C．4 D．2+3
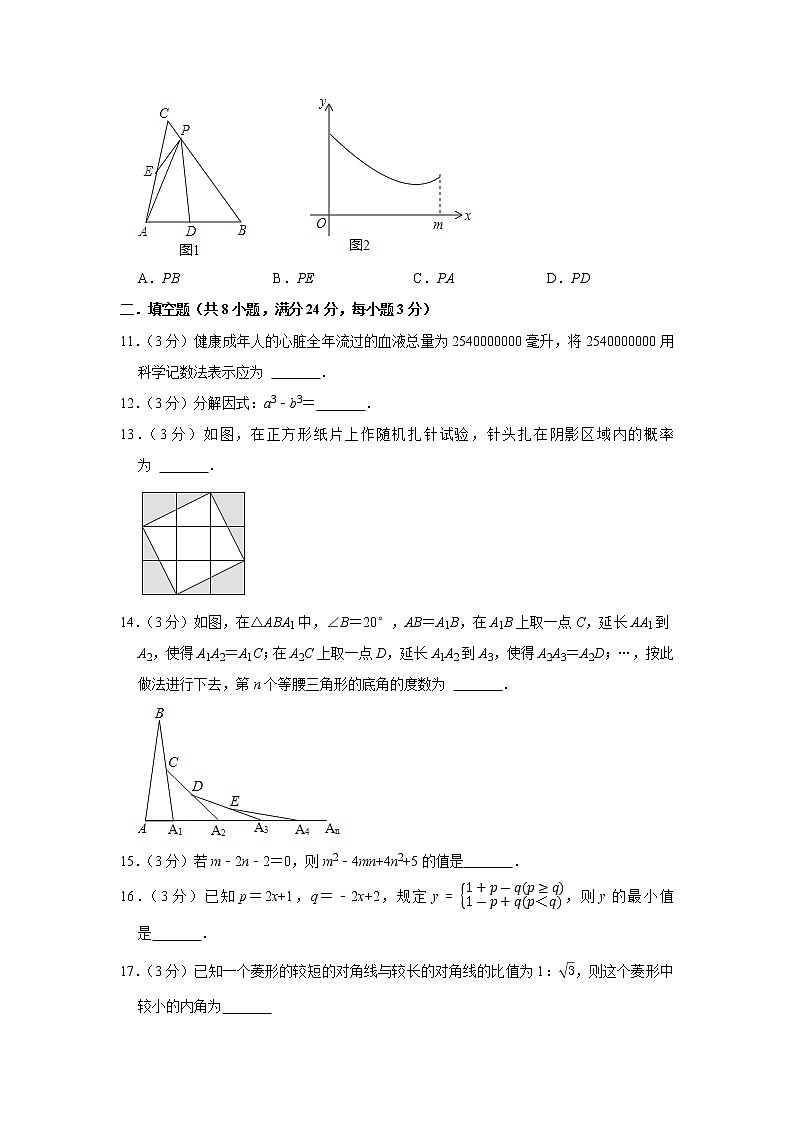
10．（3分）如图1，在△ABC中，AB＝AC，BC＝m，D，E分别是AB，AC边的中点，点P为BC边上的一个动点，连接PD，PA，PE．设PC＝x，图1中某条线段长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线可能是（　　）

A．PB B．PE C．PA D．PD
二．填空题（共8小题，满分24分，每小题3分）
11．（3分）健康成年人的心脏全年流过的血液总量为2540000000毫升，将2540000000用科学记数法表示应为 　 　．
12．（3分）分解因式：a3﹣b3＝　 　．
13．（3分）如图，在正方形纸片上作随机扎针试验，针头扎在阴影区域内的概率为 　 　．

14．（3分）如图，在△ABA1中，∠B＝20°，AB＝A1B，在A1B上取一点C，延长AA1到A2，使得A1A2＝A1C；在A2C上取一点D，延长A1A2到A3，使得A2A3＝A2D；…，按此做法进行下去，第n个等腰三角形的底角的度数为 　 　．

15．（3分）若m﹣2n﹣2＝0，则m2﹣4mn+4n2+5的值是　 　．
16．（3分）已知p＝2x+1，q＝﹣2x+2，规定y=1+p-q(p≥q)1-p+q(p＜q)，则y的最小值是　 　．
17．（3分）已知一个菱形的较短的对角线与较长的对角线的比值为1：3，则这个菱形中较小的内角为　 　
18．（3分）在△ABC中，∠BAC＝90°，BC的垂直平分线EF交BC于点F，交AB于点E，P是AC延长线上一点，连接FP，将FP绕点F逆时针旋转2α，得到FK，连接CK，如果∠B＝α（0°＜α＜90°），则CK-CPcosα⋅EF=　 　．

三．解答题（共10小题，满分76分）
19．（5分）计算：
（1）（5）2-4+327；
（2）24÷2+6（8-118）．
20．（5分）（1）x=1-y2x+3y=3
（2）7x+3y=55x+6y=-8．
21．（6分）先化简，再求值：（a+2a2-2a+84-a2）÷a-2a，其中a=3-2．
22．（6分）某教育局为了解本地八年级学生参加社会实践活动情况，随机抽查了八年级学生参加社会实践活动的天数，并用得到的数据绘制了两幅统计图，下面给出了两幅不完整的统计图：

请根据图中提供的信息，回答下列问题：
（1）所抽取的八年级学生人数是 　 　，其中a＝　 　，并写出8天所在的扇形所对圆心角的度数为 　 　．
（2）请补全条形图．
（3）如果该市共有八年级学生2000人，请你估计“活动时间不少于7天”的学生人数大约有多少人？
23．（8分）甲和乙玩一个游戏：三张大小、质地都相同的卡片上分别标有数字2，3，4（背面完全相同），现将标有数字的一面朝下，甲从中任意抽取一张，记下数字后放回洗匀，然后乙从中任意抽取一张，计算甲和乙抽得的两个数字之和．若和为奇数，则甲胜；若和为偶数，则乙胜．
（1）请你用画树状图或列表的方法，求出这两数和为6的概率；
（2）你认为这个游戏规则对双方公平吗？说明你的理由．
24．（8分）如图，在平面直角坐标系中，四边形OABC为矩形，点C、A分别在x轴和y轴的正半轴上，点D为AB的中点．一次函数y＝﹣3x+6的图象经过点C、D，反比例函数y=kx（x＞0）的图象经过点B，求k的值．

25．（8分）如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED．
（1）求证：BD＝ED．
（2）若AB＝5，BC＝7，∠ABC＝60°，求tan∠DCB的值．

26．（10分）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c的顶点坐标为D（1，4），与x轴的一个交点为A（3，0），与y轴的交点为B．
（1）求抛物线的解析式；
（2）若点P是直线AB上方抛物线上的一动点，且点P到直线AB的距离是582，求P的坐标；
（3）若点P是该抛物线上一动点，是否存在一点P，使∠PBA＝∠BAD？若存在，请写出所有P点坐标；若不存在，请说明理由．

27．（10分）父亲告诉小明：“距离地面越远，温度越低”，并且出示了下面的表格：
距离地面高度（千米）
0
1
2
3
4
5
温度（℃）
20
14
8
2
﹣4
﹣10
根据上表，父亲还给小明出了下面几个问题，你和小明一起回答：
（1）如果用h（单位：km）表示距离地面的高度，用T（单位：℃）表示温度，T如何随着h的变化而变化？写出T随着h随着h变化的函数解析式；
（2）画出函数图象；
（3）你能预测出距离地面6km的高空温度是多少吗？
28．（10分）已知在菱形ABCD中，AB＝4，∠BAD＝120°，点P是直线AB上任意一点，联结PC．在∠PCD内部作射线CQ与对角线BD交于点Q（与B、D不重合），且∠PCQ＝30°．
（1）如图，当点P在边AB上时，如果BP＝3，求线段PC的长；
（2）当点P在射线BA上时，设BP＝x，CQ＝y，求y关于x的函数解析式及定义域；
（3）联结PQ，直线PQ与直线BC交于点E，如果△QCE与△BCP相似，求线段BP的长．


参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．【解答】解：当x＜0时，﹣x＞0，
-x3y=(-x)2⋅(-xy)=-x-xy．
故选：C．
2．【解答】解：俯视图是从上面看所得到的图形，看见的棱用实线表示，看不见的用虚线表示，
故选：B．
3．【解答】解：∵将△ABC绕点C顺时针旋转得到△DEC，
∴AC＝CD，BC＝CE，AB＝DE，故A错误，C错误；
∴∠ACD＝∠BCE，
∴∠A＝∠ADC=180°-∠ACD2，∠CBE=180°-∠BCE2，
∴∠A＝∠EBC，故D正确；
∵∠A+∠ABC不一定等于90°，
∴∠ABC+∠CBE不一定等于90°，故B错误
故选：D．
4．【解答】解：(1-2nm+n)⋅m+nm2-2mn+n2
=(m+nm+n-2nm+n)⋅m+n(m-n)2
=m+n-2nm+n⋅m+n(m-n)2
=m-nm+n⋅m+n(m-n)2
=1m-n，
把m﹣n＝1代入上式，
原式＝1．
故选：C．
5．【解答】解：（0.7+0.6+0.3+0.7）÷4＝0.575．
故选：B．
6．【解答】解：当x＝﹣1时，y＝﹣（﹣1）+3＝1+3＝4，故选项A、B均不符合题意；
当x＝1时，y＝﹣1+3＝2，故选项C符合题意，选项D不符合题意；
故选：C．
7．【解答】解：设这个队胜x场，负y场，
根据题意，得x+y=83x-y=12．
故选：A．
8．【解答】解：①由抛物线y1=12(x-3)2+1与y2＝a（x+3）2﹣1知，两抛物线的顶点坐标分别是（3，1），（﹣3，﹣1），则它们关于原点对称，故①结论正确．
②由于B（5，3），且点A与点B关于直线x＝3对称，所以A（1，3），故②结论不正确．
③由于A（1，3），且点A与点C关于直线x＝﹣3对称，所以C（﹣7，3），故③结论正确．
④由抛物线y1=12(x-3)2+1=12x2﹣3x+112知，P（0，112）；由y2＝a（x+3）2﹣1＝ax2+6ax+9a﹣1知，Q（0，9a﹣1）．则PQ=112-9a+1=132-9a，故④结论不正确．
故选：B．
9．【解答】解：∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝DC，
∵AE∥DB，
∴四边形ABDE是平行四边形，
∴AB＝DE＝CD，
即D为CE中点．
∵AB＝1，
∴CE＝2，
∵AB∥CD，
∴∠ECF＝∠ABC＝45°，
过E作EH⊥BF于点H，

∵CE＝2，∠ECF＝45°，
∴EH＝CH=2，
∵∠EFC＝30°，
∴FH=3EH=6，
∴CF=2+6．
故选：A．
10．【解答】解：选项A：若y＝PB，已知BC＝m，观察图形可知PB在x＝m取得最小值为0，故A错误；
选项B：若y＝PE，E是AC边的中点，且AB＝AC，
可知PE在x=m4取得最小值，观察图2，可知选项B错误；
选项C：若y＝PA，由AB＝AC，可知PA在x=m2取得最小值，故C错误；
选项D：由前三个错误，可知本选项正确，且由题意及图形可知PD在x=3m4处取得最小值，本选项正确．
故选：D．
二．填空题（共8小题，满分24分，每小题3分）
11．【解答】解：将2540000000用科学记数法表示为2.54×109．
故答案为：2.54×109．
12．【解答】解：原式＝（a﹣b）（a2+ab+b2），
故答案为：（a﹣b）（a2+ab+b2）．
13．【解答】解：将每个小正方形的边长记为1，
则图中阴影部分面积=12×2×1×4＝4，正方形纸片的面积＝32＝9，
∴针头扎在阴影区域内的概率为49．
故答案为：49．
14．【解答】解：∵在△ABA1中，∠B＝20°，AB＝A1B，
∴∠BA1A=180°-∠B2=180°-20°2=80°，
∵A1A2＝A1C，∠BA1A是△A1A2C的外角，
∴∠CA2A1=∠BA1A2=80°2=40°；
同理可得，
∠DA3A2＝20°，∠EA4A3＝10°，
∴第n个等腰三角形的底角的度数=80°2n-1．
故答案为：80°2n-1．
15．【解答】解：∵m﹣2n﹣2＝0．
∴m﹣2n＝2．
∴原式＝（m﹣2n）2+5．
＝4+5．
＝9．
故答案为9．
16．【解答】解：∵p＝2x+1，q＝﹣2x+2，
∴当p＜q时，2x+1＜﹣2x+2，
解得：x＜14．
∴x＜14时，p＜q；当x≥14，p≥q．
∴y=1+p-q(p≥q)1-p+q(p＜q)，可化为：
y=1+2x+1-(-2x+2)=4x(x≥14)1-2x-1-2x+2=-4x+2(x＜14)，
∵y＝4x（x≥14），其函数值随自变量的增大而增大，故其在x=14时取得最小值，即y≥1；
y＝﹣4x+2（x＜14），其函数值随自变量的增大而减小，故y＞1．
∴y的最小值是1．
故答案为：1．
17．【解答】解：∵一个菱形的较短的对角线与较长的对角线的比值为1：3，
∵菱形的对角线互相垂直，
∴OAOB=13，
∴∠ABO＝30°，
∴∠ABC＝60°，
故答案为：60°

18．【解答】解：如图，

连接AF，
∵EF是BC的垂直平分线，∠BAC＝90°，
∴BF＝CF＝AF，
∴∠B＝∠BAF，
∴∠AFC＝2∠B＝2α，
∴∠AFP＝∠KFC，
∵FP＝CK，
在△AFP与△CFK中，
AF=FC∠AFP=∠CFKFP=FK
∴△AFP≌△CFK，
∴AP＝CK，
∴CK﹣CP＝AC，
过F作FD⊥AB于D，
∴FD＝cosα×EF，
∵F是BC的中点，AB⊥AC，
∴DF为△ABC的中位线，
∴DF∥AC，DF=12AC，
∴CK-CPcosα×EF=AC12AC=2．
故答案为：2．
三．解答题（共10小题，满分76分）
19．【解答】解：（1）原式＝5﹣2+3＝6；
（2）原式＝23+43-33=1733．
20．【解答】解：（1）x=1-y①2x+3y=3②，
把①代入②得：2﹣2y+3y＝3，即y＝1，
把y＝1代入①得：x＝0，
则方程组的解为x=0y=1；
（2）7x+3y=5①5x+6y=-8②，
①×2﹣②得：9x＝18，即x＝2，
把x＝2代入①得：y＝﹣3，
则方程组的解为x=2y=-3．
21．【解答】解：原式＝[a+2a(a-2)-8(a+2)(a-2)]•aa-2
=(a+2)2-8aa(a+2)(a-2)•aa-2
=(a-2)2a(a+2)(a-2)•aa-2
=1a+2，
当a=3-2时，原式=33．
22．【解答】解：（1）所抽取的八年级学生人数是：240÷40%＝600（人），
a＝1﹣（40%+20%+25%+5%）＝1﹣90%＝10%，
8天所在的扇形所对圆心角的度数为：360°×10%＝36°；
故答案为：600，10%，36°；

（2）8天的人数有：600×10%＝60（人），
补全统计图如下：


（3）根据题意得：
2000×（25%+10%+5%）＝800（人）．
答：估计“活动时间不少于7天”的学生人数大约有800人．
23．【解答】解：（1）列表如下：

2
3
4
2
2+2＝4
2+3＝5
2+4＝6
3
3+2＝5
3+3＝6
3+4＝7
4
4+2＝6
4+3＝7
4+4＝8
由表可知，总共有9种结果，其中和为6的有3种，
则这两数和为6的概率39=13；

（2）这个游戏规则对双方不公平．
理由：因为P（和为奇数）=49，P（和为偶数）=59，而49≠59，
所以这个游戏规则对双方是不公平的．
24．【解答】解：在y＝﹣3x+6中，令y＝0，则﹣3x+6＝0，
解得x＝2，
∴C（2，0），
∴B（2，k2），
∴A（0，k2），
∵点D为AB的中点，
∴点D（1，k2），
∵点D在直线y＝﹣3x+6上，
∴k2=-3×1+6，
∴k＝6．
25．【解答】（1）证明：∵∠1＝∠2，
∴AD=DC，
∴AD＝DC，
∵四边形ABCD内接于⊙O，
∴∠BAD+∠BCD＝180°，
∵∠ECD+∠BCD＝180°，
∴∠BAD＝∠ECD，
在△ABD和△CED中，
AD=DC∠BAD=∠ECDAB=CE，
∴△ABD≌△CED（SAS），
∴BD＝ED；
（2）解：过点D作DM⊥BE于M，
∵AB＝5，BC＝7，CE＝AB＝5，
∴BE＝BC+EC＝12，
∵BD＝ED，DM⊥BE，
∴BM＝ME=12BE＝6，
∴CM＝BC﹣BM＝1，
∵∠ABC＝60°，∠1＝∠2，
∴∠2＝30°，
∴DM＝BM•tan∠2＝6×33=23，
∴tan∠DCB=DMCM=23．

26．【解答】解：（1）∵抛物线y＝ax2+bx+c的顶点坐标为D（1，4），
∴设抛物线的解析式为：y＝a（x﹣1）2+4，
∵抛物线经过点A（3，0），
∴0＝a（3﹣1）2+4，解得，a＝﹣1，
∴抛物线的解析式为：y＝﹣x2+2x+3①；

（2）如图1，连接PA，过点P作PC⊥x轴，交AB于点C，
∵A（3，0），B（0，3），
∴直线AB的解析式为：y＝﹣x+3，且AB=32，

设点P（m，﹣m2+2m+3），则点C（m，﹣m+3），
∴PC＝（﹣m2+2m+3）﹣（﹣m+3）＝﹣m2+3m，
∴S△ABP=12PC⋅(xA-xB)=12(-m2+3m)(3-0)=32(-m2+3m)，
设d为点P到直线AB距离是582，
又∵S△ABP=12AB⋅d=12×32×582=158，
∴32(-m2+3m)=158，解得m1=12，m2=52，
∴点P的坐标为(12，154)或(52，74)；

（3）存在，理由：
①当点P在x轴上方时，
如图2，延长AD交y轴于点M，过点M作MG⊥AB交于点G，过点A作AH∥BP于y轴于点H，则∠BAD＝∠BAH，

由点A、B、D的坐标知，OB＝OA＝3，∠OBA＝∠OAB＝45°，
由点A、D的坐标得，直线AD的表达式为y＝﹣2x+6，则点M（0，6），
则BM＝6﹣3＝3，AM＝35，
在△AGM中，∠GBM＝∠OBA＝45°，则BG＝MG=22MB=322，
则tan∠BAD=GMAG=32232+322=13，
∵∠PBA＝∠BAD，∠BAD＝∠BAH，
∴∠PBA＝∠BAH＝∠BAD，
∴tan∠BAH=13，
在△BAH中，∠HBA＝45°，tan∠BAH=13，AB＝32，
过点H作HR⊥AB于点R，设RH＝x＝BR，则AR＝3x，
则AB＝32=AR+BR＝4x，解得x=324，
则BH=2x=32，故点H的坐标为（0，32），
由点A、H的坐标得：直线AH的表达式为y=-12x+32，
∵AH∥BP，
故设直线BP的表达式为y=-12x+t，
将点B的坐标代入上式得：3＝t，解得t＝3，
故直线BP的表达式为y=-12x+3②，
联立①②并解得x=52y=74（不合题意的值已舍去），
故点P的坐标为（52，74）；
②当点P（P′）在x轴下方时，
则PB∥AD，同理可得，直线BP′的表达式为y＝﹣2x+6③，
联立①③并解得x=4y=-5（不合题意的值已舍去），
故点P的坐标为（52，74）或（4，﹣5）．
27．【解答】解：（1）根据表中数据的变化规律，T随着h的增大而减小，
设T＝kh+b，把（0，20），（1，14）代入得：b=20k+b=14，
解得：k=-6b=20，
∴T＝﹣6h+20．
（2）如图，根据点（0，20），（103，0）画出图象．

（3）当h＝6时，T＝﹣6×6+20＝﹣16．
∴距离地面6km的高空温度是﹣16℃．
28．【解答】解：（1）如图1中，作PH⊥BC于H．

∵四边形ABCD是菱形，
∴AB＝BC＝4，AD∥BC，
∴∠A+∠ABC＝180°，
∵∠A＝120°，
∴∠PBH＝60°，
∵PB＝3，∠PHB＝90°，
∴BH＝PB•cos60°=32，PH＝PB•sin60°=332，
∴CH＝BC﹣BH＝4-32=52，
∴PC=PH2+CH2=(332)2+(52)2=13．

（2）如图1中，作PH⊥BC于H，连接PQ，设PC交BD于O．
∵四边形ABCD是菱形，
∴∠ABD＝∠CBD＝30°，
∵∠PCQ＝30°，
∴∠PBO＝∠QCO，
∵∠POB＝∠QOC，
∴△POB∽△QOC，
∴POQO=BOCO，
∴OPBO=QOCO，
∵∠POQ＝∠BOC，
∴△POQ∽△BOC，
∴∠OPQ＝∠OBC＝30°＝∠PCQ，
∴PQ＝CQ＝y，
∴PC=3y，
在Rt△PHB中，BH=12x，PH=32x，
∵PC2＝PH2+CH2，
∴3y2＝（32x）2+（4-12x）2，
∴y=3x2-12x+483（0≤x＜8）．

（3）①如图2中，若直线QP交直线BC于B点左侧于E．

此时∠CQE＝120°，
∵∠PBC＝60°，
∴△PBC中，不存在角与∠CQE相等，
此时△QCE与△BCP不可能相似．

②如图3中，若直线QP交直线BC于C点右侧于E．

则∠CQE＝∠B＝QBC+∠QCP＝60°＝∠CBP，
∵∠PCB＞∠E，
∴只可能∠BCP＝∠QCE＝75°，
作CF⊥AB于F，则BF＝2，CF＝23，∠PCF＝45°，
∴PF＝CF＝23，
此时PB＝2+23，
③如图4中，当点P在AB的延长线上时，

∵△QCE与△BCP相似，
∴∠CQE＝∠CBP＝120°，
∴∠QCE＝∠PCB＝15°，
作CF⊥AB于F．
∵∠FCB＝30°，
∴∠FCP＝45°，
∴BF=12BC＝2，CF＝PF＝23，
∴PB＝23-2．
综上所述，满足条件的PB的值为2+23或23-2．