河北省衡水市深州市2021-2022学年高一下学期期末考试数学试卷

2021~2022学年深州市中学高一年级期末考试

数学试卷

一､单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 若，则在复平面内复数z对应的点位于（    ）

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

2. 已知集合，则（    ）

A.  B.  C.  D.

3. 已知，，，则的大小关系是

A.  B.  

C.  D.

4. 小张一星期的总开支分布如图所示，一星期的食品开支如图所示，则小张一星期的肉类开支占总开支的百分比约为（    ）

A. 10% B. 8% C. 5% D. 4%

5. 若，则（    ）

A.  B.  C.  D.

6. 在中，若，则的形状一定是（    ）

A 等腰三角形 B. 直角三角形

C. 正三角形 D. 不能确定

7. 已知四边形的对角线交于点O，E为的中点，若，则（    ）

A.  B.  C.  D. 1

8. 已知正数x，y满足，则的最小值为（    ）

A. 4 B. 5 C. 6 D. 7

二､多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 在中，，则的面积可以是（    ）

A.  B. 1 C.  D.

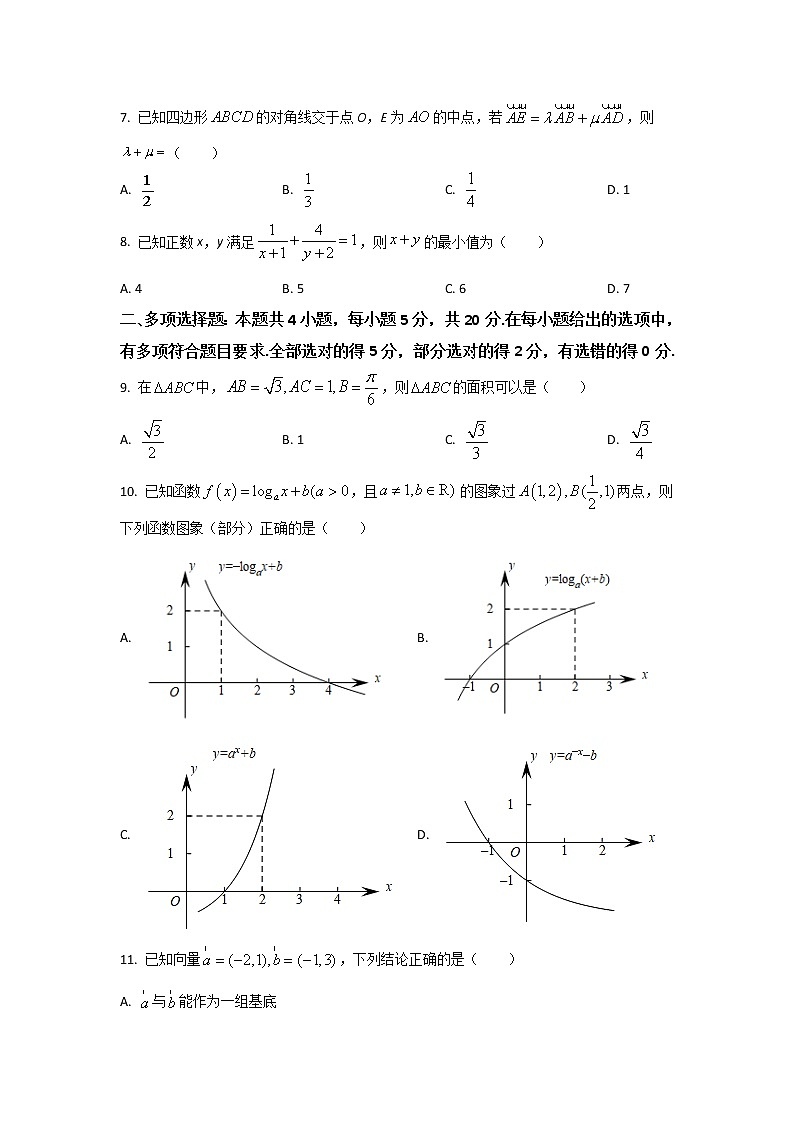
10. 已知函数，且的图象过两点，则下列函数图象（部分）正确的是（    ）

A.  B.

C.  D.

11. 已知向量，下列结论正确的是（    ）

A. 与能作为一组基底

B. 与同向的单位向量的坐标为

C. 与夹角的正弦值为

D. 若满足，则

12. 如图，将正方形沿对角线折成直二面角，则下列四个结论中正确的是（    ）

A.

B. 是等边三角形

C. 与所成的角为

D. 与平面所成角为

三､填空题：本题共4小题，每小题5分，共20分.

13. 已知是虚数单位，复数z满足，则复数z的模为___________.

14. 抽样统计某位射击运动员10次的训练成绩分别为，则该运动员这10次成绩的分位数为___________，中位数为___________.

15. 在三棱锥P-ABC中，PA⊥AB，AC⊥AB，PA=3，AC=4，PC=5，且三棱锥P-ABC的外接球的表面积为28π，则AB=______．

16. 随着生活水平的不断提高，人们更加关注健康，重视锻炼.通过“小步道”，走出“大健康”，健康步道成为引领健康生活的一道亮丽风景线.如图，为某区的一条健康步道，其中为线段，三点共线，是以为直径的半圆，，.则该健康步道的长度为___________.

四､解答题：本题共6小题，共70分，解答应写出必要的文字说明､证明过程及演算步骤.

17. 有两位射击运动员在一次射击测试中各射靶7次，每次命中的环数如下：

甲  6  9  7  8  8  5  6

乙  a  3  9  8  9  6  4

经计算可得甲、乙两名射击运动员的平均成绩是一样的．

（1）求实数a的值；

（2）请通过计算，判断甲、乙两名射击运动员哪一位的成绩更稳定？

18. 已知向量，向量的夹角的正切值为，．

（1）求向量的模；

（2）若，求实数k的值．

19. 已知函数．

（1）求函数的单调区间；

（2）求函数图象的对称中心的坐标和对称轴方程．

20. 如图，在四棱锥中，底面是矩形，，是棱上一点，且平面.

（1）证明：平面平面；

（2）求直线与平面所成角的正弦值.

21. 在中，内角所对的边分别为，且满足．

（1）求的值；

（2）已知面积为，求a的值．

22. 已知函数是偶函数．

（1）求实数值；

（2）若函数的最小值为，求实数的值；

（3）当为何值时，讨论关于的方程的根的个数．

答案

1-8 BDBAC  AAC  9.AD  10.ABD  11.ACD  12.ABC

13.

14.   ①. ##    ②. ##

15.

16.

17.（1）10；    （2）甲的成绩比乙更稳定.

18.（1）；（2）7.

19.（1）增区间为，减区间为   

（2）对称中心的坐标为；对称轴方程为

20. （1）

在矩形中，所以，

平面平面平面，

，

在中，为中点，

，

，即，

又平面平面，

平面，

又平面平面平面；

（2）

21.（1）2    （2）1

22.（1）   

（2）   

（3）当时，方程有一个根；

当时，方程没有根；

当或或时，方程有两个根；

当时，方程有三个根；

当时，方程有四个根．