2022年四川省乐山市五通桥区中考适应性考试数学试题(word版含答案)

五通桥区2022届初三毕业复习适应性检测题

数学

2022.4

本试题卷分第一部分（选择题）和第二部分（非选择题），共6页．考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效．满分150分．考试时间120分钟．

考试结束后，将本试题卷和答题卡一并交回．考生作答时，不能使用任何型号的计算器．

第一部分（选择题  共30分）

注意事项：

1．选择题必须使用2B铅笔将答案标号填涂在答题卡对应题目标号的位置上．

2．本部分共10小题，每小题3分，共30分．

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项符合题目要求．

1．在实数，－2，0，中，最小的实数是（    ）

A．－2    B．0    C．    D．

2．如图（1），，∠B=68°，∠E=20°，则∠D的度数为（    ）

A．28°    B．38°    C．48°    D．88

3．地球的体积约为立方千米，太阳的体积约为立方千米，地球的体积与太阳体积的比大约是0.00000071．其中的“比值”用科学记数法表示为（    ）

A．  B．  C．   D．

4．把进行因式分解，结果正确的是（    ）

A．      B．

C．       D．

5．某体校要从四名射击选手中选拔一名参加省体育运动会，选拔赛中每名选手连续射靶10次，他们各自的平均成绩及其方差如表所示：

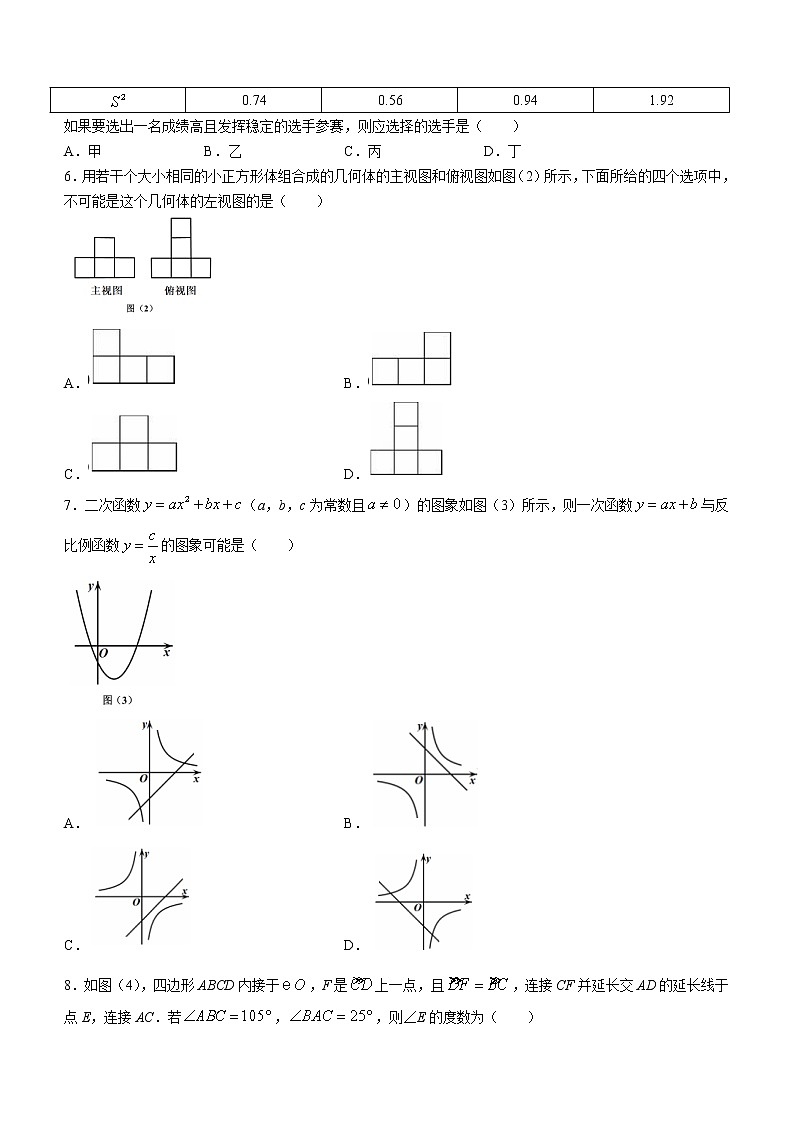
如果要选出一名成绩高且发挥稳定的选手参赛，则应选择的选手是（    ）

A．甲    B．乙    C．丙    D．丁

6．用若干个大小相同的小正方形体组合成的几何体的主视图和俯视图如图（2）所示，下面所给的四个选项中，不可能是这个几何体的左视图的是（    ）

A．      B．

C．      D．

7．二次函数（a，b，c为常数且）的图象如图（3）所示，则一次函数与反比例函数的图象可能是（    ）

A．     B．

C．      D．

8．如图（4），四边形ABCD内接于，F是上一点，且，连接CF并延长交AD的延长线于点E，连接AC．若，，则∠E的度数为（    ）

B

A．45°    B．50°    C．55°    D．60°

9．若锐角满足且，则的范围是（    ）

A． B． C． D．

10．如图（5），抛物线与x轴交于A、B两点，P是以点为圆心，2为半径的圆上的动点，Q是线段PA的中点，连结OQ．则线段OQ的最大值是（    ）

A．    B．   C．3    D．4

第二部分（非选择题共  120分）

注意事项

1．考生使用0.5mm黑色墨汁签字笔在答题卡上题目所指示的答题区域内作答，答在试题卷上无效．

2．作图时，可先用铅笔画线，确认后再用0.5mm黑色墨汁签字笔描清楚．

3．解答题应写出文字说明、证明过程或推演步骤．

4．本部分共16小题，共120分．

二、填空题：本大题共6小题，每小题3分，共18分．

11．计算：______．

12．如果关于x的一元二次方程有两个不相等的实根，那么k的取值范围是______．

13．如图（6），已知圆锥的高为，高所在直线与母线的夹角为30°，圆锥的侧面积为______．

14．某居民小区共有300户家庭，有关部门对该小区的自来水管网系统进行改造，为此该部门通过随机抽样，调查了其中20户家庭，统计了这20户家庭的月用水量，如下表：

根据上述数据，估计该小区300户家庭的月总用水量约为______m3．

15．已知方程组的解为，则方程组的解为______．

16．如图（7），为等腰直角三角形，，，E为AB上任意一动点，以CE为斜边作等腰，连接AD，下列说法：

①；②；③；④；⑤四边形ABCD的面积有最大值，且最大值为。其中，正确的结论是______．

三、本大题共3小题，每小题9分，共27分．

17．计算：．

18．如图（8），在平面直角坐标系中，已知的三个顶点的坐标分别为，，．

（1）已知点的坐标为，画出经过平移后得到的，写出顶点，的坐标；

（2）将绕着点O按顺时针方向旋转90°得到，写出的各顶点的坐标；

（3）动点P在y轴上，画出为最小值时点P的位置，并求出的最小值．

19．如图（9），在中，∠B=90°，点E是AC的中点，，∠BAC的平分线AD交BC于点D，作，连接DE并延长交AF于点F，连接FC．求证：四边形ADCF是菱形．

四、本大题共3小题，每小题10分，共30分．

20．某蔬菜店以每千克2元的价格购进某种绿色蔬菜若干千克，然后以每千克4元的价格出售，每天可售出100千克．通过调查发现，这种蔬菜每千克的售价每降低0.1元，每天可多售出20千克，为保证每天至少售出260千克，蔬菜店决定降价销售．若将这种蔬菜每千克售价降低x元．

（1）每天的销售量是______千克（用含x的代数式表示）；

（2）销售这种蔬菜要想每天盈利300元，每千克的售价需降低多少元？

21．有六张完全相同的卡片，分A、B两组，每组三张，在A组的卡片上分别画上“√、×、√”，B组的卡片上分别画上“√、×、×”，如图（10-1）所示。

（1）若将卡片无标记的一面朝上摆在桌上，再发布从两组卡片中随机各抽取一张，求两张卡片上标记都是√的概率（请用树形图法或列表法求解）

（2）若把A、B两组卡片无标记的一面对应粘贴在一起得到3张卡片，其正反面标记如图（10-2）所示，将卡片正面朝上摆放在桌上，并用瓶盖盖住标记。

①若随机揭开其中一个盖子，看到的标记是√的概率是多少；

②若揭开盖子，看到的卡片正面标记是√后，猜想它的反面也是√，求猜对的概率。

22．如图（11），已知中，，CD是斜边AB上的中线，过点A作，AE分别与CD、CB相交于点H、E，．

（1）求的值；

（2）如果，求BE的值．

五、本大题共2小题，每小题10分，共20分．

23．如图（12），在直角坐标系中，直线与反比例函数的图象交于关于原点对称的A，B两点，已知A点的纵坐标是3．

（1）求反比例函数的表达式；

（2）将直线向上平移后与反比例函数在第二象限内交于点C，如果的面积为48，求平移后的直线的函数表达式．

24．如图（13），以的直角边AB为直径作，交斜边AC于点D，点E为OB的中点，连接CE并延长交于点F，点F恰好落在中点，连接AF并延长与CB的延长线相交于点G，连接OF．

（1）求证：；

（2）若，求DC的长．

六、本大题共2小题，第25题12分，第26题13分，共25分．

25．用矩形ABCD作如下探究活动：将一个矩形ABCD绕点A顺时针旋转，得到矩形，连接BD．

【探究1】如图（14-1），当时，点恰好在DB延长线上．若，求BC的长．

【探究2】如图（14-2），连接，过点作交BD于点M．线段与DM相等吗？请说明理由．

【探究3】在探究2的条件下，射线DB分别交，于点P，N（如图（14-3）），发现线段DN，MN，PN存在一定的数量关系，请写出这个关系式，并加以证明．

26．如图（15），已知抛物线经过点，和．CD垂直于y轴，交抛物线于点D，DE垂直与x轴，垂足为E，l是抛物线的对称轴，点F是抛物线的顶点．

（1）求出二次函数的表达式以及点D的坐标；

（2）若沿x轴向右平移到其直角边OC与对称轴l重合，再沿对称轴l向上平移到点C与点F重合，得到，求此时矩形OCDE重叠部分的图形的面积；

（3）若沿x轴向右平移t个单位长度得到，与重叠部分的图形面积记为S，求S与t之间的函数表达式，并写出自变量t的取值范围．

五通桥区2022年中考复习调研考试

数学试题参考答案及评分意见

一、选择题：每小题3分，10小题，共计30分

1．A  2．C  3．B  4．C  5．B

6．D  7．C  8．B  9．D  10．A

二、填空题：每小题3分，6小题，共计18分

11．4  12．  13．  14．2790  15．  16．①④⑤

三、本大题共3小题，每小题9分，共27分

17．解：原式

18．（1）如图，为所作，，；

（2）如图，为所作，，，，

（3）如图，P为所作，

19．证明：∵，∴，

在和中，

∴，∴，又，

∴四边形ADCF是平行四边形，∵，，

∴，∵AD平分∠CAB，

∴

∴，∴四边形ADCF是菱形．

四、本大题共3小题，每小题10分，共30分

20，解：（1）

（2）根据题意，得

解得，．

∵要保证每天至少售出260千克，即，得．

∴．

故每千克的售价降低1元．

21．（1）根据题意，可列表如下：

∴．

（2）①∵根据题意，三张卡片正面的标记有三种可能，分别为“√”、“×”、“√”，∴随机揭开其中一个盖子，看到的标记是“√”的概率为．

②∵正面标记为为“√”的卡片，它的反面标记只有两种情况，分别为“√”和“×”，∴猜对反面也是“√”的概率为．

22．（1）∵，CD是AB上的中线

∴，∴，

又∵

∴

∴

又∵

∴

（2）∵

∴，

∴；

∴；∴

五、本大题共2小题，每小题10分，共20分．

23．解：（1）∵A在，A点的纵坐标是3，则得：，即．

∵点在反比例函数的图象上，

∴，∴反比例函数的表达式为．

（2）若直线向上平移后交y轴于点

∵与反比例函数在第二象限内交于点C

∴

又∵A、B两点关于原点对称，∴点，则

∴

又∵

∴，则

∴平移后的直线的函数表达式

24．（1）证明：∵以的直角边AB为直径作，点F恰好落在中点

∴，∴，∵，∴，

∴，∴，∴FO是的中位线，∴；

（2）解：在和中，

∴（ASA），

∴，则，

连接DB，∵AB为直径，∴，

又∵，

∴，得即

∴

六、本大题共2小题，第25小题12分，第26小题13分，共计25分

25．解：（1）∵矩形ABCD绕A旋转得，，由题易证

∴

设，得

解得，（不合题意，舍去）

∴

（2）相等

证明：连接

∵矩形ABCD绕A旋转得

∴

∴

又∵

∴

又∵

∴

∴

（3）关系式为

证明：在和中

，

∴

∴，即

26．解：（1）∵过点，．

∴设抛物线的解析式为，∵在抛物线上，

∴，即

∴设抛物线的解析式为

整理得

∵CD垂直于y轴，，得

∴，解得，（舍）

∴，则∴

（2）如图1，

∵点F是抛物线的顶点，

∴，∴，由题得，∴

∴，得

∴

（3）①当时，如图2，

由题得，∴，∴，

∴，∴，

②当时，如图3，

由题得，

∴，∴，得

作，得

∴得

∴

∴得

∴

∴当时，，

当时，