2022年河南省信阳市普通高中中考数学模拟试卷（一）（含解析）

2022年河南省信阳市普通高中中考数学模拟试卷（一）

一、选择题（本大题共10小题，共30分）

1. 的平方根是

A.  B.  C.  D.

2. 进入春季，由于气温回升，春暖花开很多花粉随风飞扬，伴随细菌病毒、支原体感染都会引起呼吸系统感染，呼吸系统感染进入高发期，今年花粉感染较为突出，及时补充水分，勤洗手，出行戴口罩是有效的防范措施，某种花粉的直径约为，用科学记数法表示为

A.  B.  C.  D.

3. 将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，下列编号为，，，的小正方形中不能剪去的是

A.
B.
C.
D.

4. 下列运算正确的是

A.  B.
C.  D.

5. 将一块等腰直角三角板与一把直尺如图放置，若，则的度数为

A.
B.
C.
D.

6. 如图，在四边形中，，我们把这种两组邻边分别相等的四边形叫做筝形．根据学习平行四边形性质的经验，有同学得出如下筝形的性质，你认为其中不正确的是

A. 两组邻边分别相等
B. 有一组对角相等
C. 两条对角线相互垂直平分
D. 一条对角线被另一条对角线垂直平分
 

7. 定义运算：例如：则方程的根的情况为

A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 无实数根 D. 无法确定

8. 第届冬奥会期间，小牛收集到张卡片，正面图案如图所示，它们除此之外完全相同，把这张卡片背面朝上洗匀后摸出张，放回洗匀再摸出一张，则这两张卡片正面图案恰好是“单板滑雪”和“双板滑雪”的概率是

A.  B.  C.  D.

9. 如图，在矩形中，，以点为圆心，长为半径画弧，交边于点，且为中点，则图中阴影部分的面积为

A.
B.
C.
D.

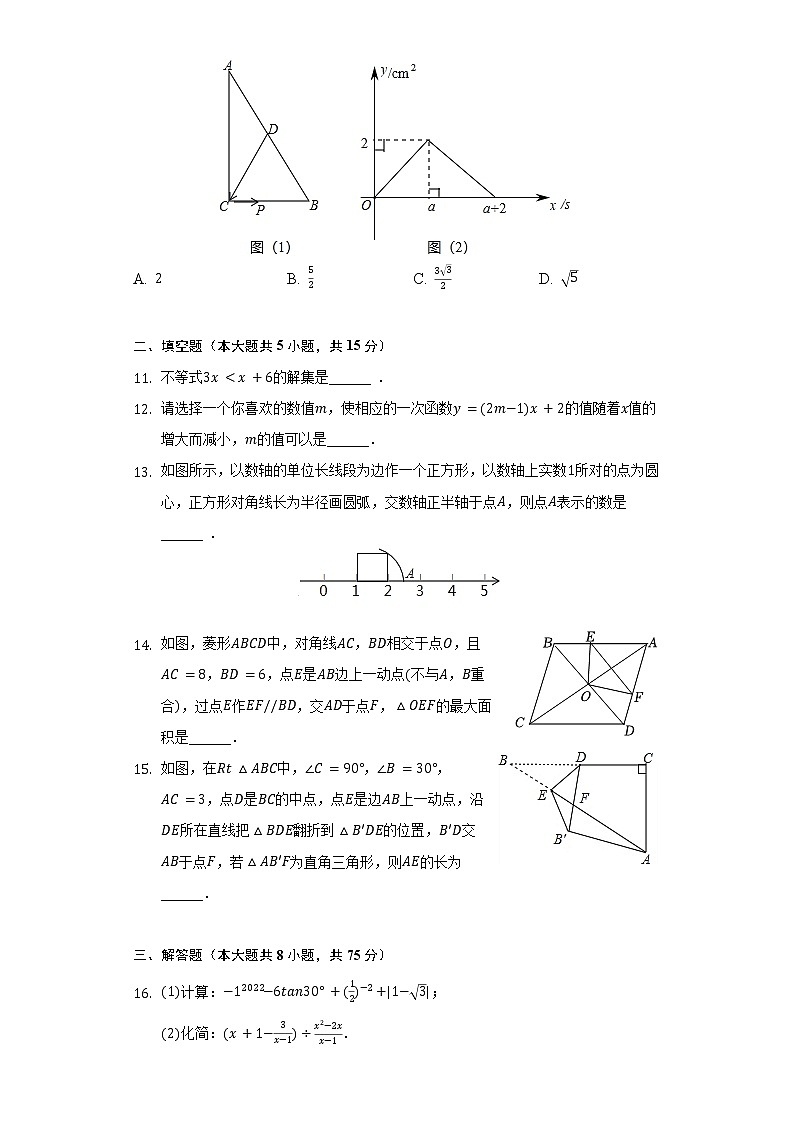
10. 如图，中，，是中线，点从点出发，沿的方向以的速度运动到点图是点运动时，的面积随时间变化的图象，则的值为

A.  B.  C.  D.

二、填空题（本大题共5小题，共15分）

11. 不等式的解集是______ ．
12. 请选择一个你喜欢的数值，使相应的一次函数的值随着值的增大而减小，的值可以是______．
13. 如图所示，以数轴的单位长线段为边作一个正方形，以数轴上实数所对的点为圆心，正方形对角线长为半径画圆弧，交数轴正半轴于点，则点表示的数是______ ．

14. 如图，菱形中，对角线，相交于点，且，，点是边上一动点不与，重合，过点作，交于点，的最大面积是______．
15. 如图，在中，，，，点是的中点，点是边上一动点，沿所在直线把翻折到的位置，交于点，若为直角三角形，则的长为______．

三、解答题（本大题共8小题，共75分）

16. 计算：；
    化简：．
17. 践行文化自信，让中华文化走向世界．习近平指出，“提高国家文化软实力，要努力展示中华文化独特魅力”，要“把跨越时空、超越国度、富有永恒魅力、具有当代价值的文化精神弘扬起来，把继承传统优秀文化又弘扬时代精神、立足本国又面向世界的当代中国文化创新成果传播出去”郑州市甲、乙两校的学生人数基本相同，为了解这两所学校学生的中华文化知识水平，在同一次知识竞赛中，从两校各随机抽取了名学生的竞赛成绩进行调查分析，其中甲校已经绘制好了条形统计图，乙校只完成了一部分如图．
    甲校：
    乙校：
    
    请根据乙校的数据补全条形统计图；
    两组样本数据的平均数、中位数、众数如下表所示，请补全表格：

请判断哪所学校学生的中华文化知识水平更好一些．并根据中的数据说明理由；
为进一步提高两所学校学生的中华文化知识水平，请你提出一条合理化建议．

18. 如图，矩形的边在轴上，为对角线，的交点，点，的坐标分别为，．
    反比例函数在第三象限的图象经过点，求这个函数的解析式；
    点是否在函数的图象上？说明理由；
    一次函数的图象经过点，点，根据图象直接写出不等式的解集．
19. 著名的永泰寺塔，位于河南登封嵩山南麓，建于盛唐时期，为第五批全国重点文物保护单位，永泰寺塔是一座单层密檐式砖塔，采用青砖黄泥垒砌而成，平面呈方形，塔的外壁敷有一层薄薄的白灰，塔身高耸，塔基底边长，永泰寺塔，自下而上每层高度均匀递减、塔檐逐渐内收，外轮廓的连线呈柔和的抛物线状，塔室内部仍为方形，空筒状，塔刹由仰莲、五重相轮等组成，其精美的造型，是我国现存唐塔塔刹中的佼佼者．“综合与实践”小组开展了测量“永泰寺塔”高度的实践活动，他们设计了两个测量方案如表，经过老师与小组利用课余时间实地考察放弃了方案一，采用了方案二，他们在“永泰寺塔”底部所在的水平地面上选取两个不同的测点，分别测量了“永泰寺塔”顶端的仰角以及这两个测点之间的距离，为了减小测量误差，小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果填入表格，测量数据如表：

“综合与实践”小组为什么放弃方案一，你认为原因可能是什么？写出一条即可
请你根据他们的测量数据计算“永泰寺塔”的高度．参考数据：，，

20. 已知：如图，中，，，求作：线段，使得点在线段上，且．
    作法：以点为圆心，长为半径画圆；
    以点为圆心，长为半径画弧，交于点不与点重合；
    连接交于点，线段就是所求作的线段．
    使用直尺和圆规，依作法补全图形保留作图痕迹：
    说明的理由．
21. 年月日，中共中央办公厅、国务院办公厅印发关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见某学校积极响应“双减”政策，为了丰富学生校园生活，经研究决定准备购买一批体育健身器材．其中需要购买甲、乙两种品牌的篮球；购买甲品牌的篮球个，乙品牌的篮球个．共花费元，已知购买一个乙品牌的篮球比购买一个甲品牌的篮球多花元
    求购买一个甲品牌、一个乙品牌的篮球各需多少元？
    经过一段时间调查，发现喜欢篮球的学生较多，于是，学校决定再次购进甲、乙两种品牌篮球共个，正好“某宝”对商品促销．甲品牌篮球售价比第一次购买时降低元，乙品牌篮球按第一次购买时售价的折出售，如果学校此次购买甲、乙两种品牌篮球的总费用不超过第一次花费的，且保证这次购买的乙品牌篮球不少于个，则这次学校有几种购买方案？
    直接写出学校在第二次购买活动中至少需要多少资金？
22. 已知抛物线的对称轴为直线，图象与轴交于点．
    求抛物线的函数表达式．
    若把抛物线的图象沿轴平移个单位长度，在自变量的值满足的情况下，与其对应的函数值的最小值为，求的值．
     

23. 提出问题：在综合与实践课上，老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合，并让一个三角板固定，另一个绕直角顶点旋转”为主题开展数学活动．
    如图，三角板和三角板都是等腰直角三角形，，点，分别为，的中点．
    如图，将点、点重叠合并在一起，记作点，点，分别落在边，上，连接，记的中点为点，试判断线段与的数量关系和位置关系．
    
    探究交流：感恩小组发现，，，并展示了如下的证明方法：

反思拓展：

上述证明过程中的“依据”，“依据”分别是指什么？
试判断图中，与的位置关系，请直接回答，不必证明；
“责任”小组在探究时，把绕点逆时针方向旋转到如图的位置，发现是等腰直角三角形，请你给出证明；
“坚持”小组的同学进行“固定变量”探究，令，时，把绕点在平面内自由旋转，的面积是否发生变化，若不变，请直接写出的面积；若变化，的面积是否存在最大与最小？若存在，请直接写出面积的最大值与最小值．
答案和解析

1.【答案】

【解析】解：，
的平方根是为．
故选D．
直接根据平方根的概念即可求解．
本题主要考查了平方根的概念，熟记平方根的定义是解题的关键．
 

2.【答案】

【解析】解：．
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数，当原数绝对值时，是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
 

3.【答案】

【解析】解：如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，编号为、、、的小正方形中不能剪去的是；
故选：．
根据正方体的展开图中每个面都有唯一的一个对面进行判断，可得答案．
本题考查了展开图折叠成几何体，利用正方体的展开图中每个面都有唯一的一个对面是解题关键．
 

4.【答案】

【解析】解：，故选项A不符合题意；
，故选项B不符合题意；
，故选项C不符合题意；
，故选项D符合题意；
故选：．
根据平方差公式可以判断，根据积的乘方可以判断，根据完全平方公式可以判断，根据单项式乘单项式可以判断．
本题考查整式的混合运算，解答本题的关键是明确整式混合运算的计算方法．
 

5.【答案】

【解析】

【分析】
此题主要考查了平行线的性质，要熟练掌握，解答此题的关键是要明确： 定理 ：两条平行线被第三条直线所截，同位角相等．简单说成：两直线平行，同位角相等． 定理 ：两条平行线被地三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补． 定理 ：两条平行线被第三条直线所截，内错角相等．简单说成：两直线平行，内错角相等．首先根据 ，判断出 ，进而求出 的度数；然后对顶角相等，求出 的度数，再根据 ，求出 的度数为多少即可．
【解答】
解：如图 ，

，
，
，
，
，
．
故选 B ．   

6.【答案】

【解析】解：两组邻边分别相等；正确；
B.有一组对角相等；正确；
C.两条对角线相互垂直平分；不正确；
D.一条对角线被另一条对角线垂直平分；正确；
故选：．
根据筝形的性质对各个选项进行判断，即可得出结论．
此题考查了筝形的性质；熟记筝形的性质是解题的关键．
 

7.【答案】

【解析】解：由新定义得，
，
方程有两个不相等的实数根．
故选：．
利用新定义得到，然后利用可判断方程根的情况．
本题考查了根的判别式：一元二次方程的根与有如下关系：当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程无实数根．
 

8.【答案】

【解析】解：设单板滑雪用表示，花样滑冰用表示，双板滑雪用表示，冰球用表示，
树状图如下：

由上可得，一共有种可能性，其中这两张卡片正面图案恰好是“单板滑雪”和“双板滑雪”的可能有种，
故这两张卡片正面图案恰好是“单板滑雪”和“双板滑雪”的概率是，
故选：．
根据题意，可以画出相应的树状图，从而可以求得这两张卡片正面图案恰好是“单板滑雪”和“双板滑雪”的概率．
本题考查列表法与树状图法，解答本题的关键是明确题意，画出相应的树状图．
 

9.【答案】

【解析】解：在中，，
，，
，
图中阴影部分的面积，
故选：．
根据直角三角形的性质得到，得到，根据勾股定理求出，根据扇形面积公式、三角形面积公式计算即可．
本题考查的是扇形面积计算、矩形的性质，掌握扇形面积公式是解题的关键．
 

10.【答案】

【解析】解：由点的运动可知，，，且当点运动到点时，的面积为，
过点作于点，

，即，
是中线，即点是的中点，
是的中位线，
，
，
在中，由勾股定理可知，，
．
故选：．
由点的运动可知，，，且当点运动到点时，的面积为，过点作于点，可得，则，最后根据勾股定理可知，所以．
本题考查了动点的函数图象问题，涉及三角形中位线定理，勾股定理等内容，关键是结合图得出的长度．
 

11.【答案】

【解析】解：，
移项，得，
合并同类项，得，
系数化成，得，
故答案为：．
移项，合并同类项，系数化成即可．
本题考查了解一元一次不等式，能正确根据不等式的性质进行变形是解此题的关键．
 

12.【答案】答案不唯一

【解析】解：根据题意得：
解得：，则的值可以是答案不唯一．
根据一次函数的值随着值的增大而减小，可得到，即可求得的范围．
本题主要考查了一次函数的性质，根据一次函数的一次项系数的符号判断函数的增减性．
 

13.【答案】

【解析】解：数轴上正方形的对角线长为：，
由图中可知和之间的距离为．
点表示的数是．
故答案为：．
先根据勾股定理求出正方形的对角线长，再根据两点间的距离公式为：两点间的距离较大的数较小的数，便可求出和之间的距离，进而可求出点表示的数．
本题考查的是勾股定理及两点间的距离公式，本题需注意：知道数轴上两点间的距离，求较小的数，就用较大的数减去两点间的距离．
 

14.【答案】

【解析】解：设与相交于点，

设，
四边形是菱形，
，，，
，
，
，
，，，
∽，
，
，
，，
，
的面积


，
当时，的面积最大，且最大值为，
故答案为：．
设与相交于点，设，根据菱形的性质可得，，，从而求出，再利用平行线的性质可得，，，从而证明字模型相似三角形∽，利用相似三角形的性质可得，，从而可得，然后利用三角形的面积公式可得的面积，即可解答．
本题考查了菱形的性质，相似三角形的判定与性质，二次函数的最值，熟练掌握相似三角形的判定与性质，以及二次函数的最值是解题的关键．
 

15.【答案】或

【解析】

【分析】
本题考查翻折变换、勾股定理、全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想解决问题，属于中考常考题型．
【解答】
解：如图 中，当 时．

在 中， ， ，
， ，
，
，
，
，
，
，
，设 ，
在 中， ，
，
，
．

如图 中，当 时，作 交 的延长线于 设 ．

， ，
≌ ，
，
，
，
在 中， ， ，
在 中， ，
，
解得 ，
综上所述，满足条件的 的值为 或 ．
故答案为 或 ．   

16.【答案】解：


；




．

【解析】根据有理数的乘方，特殊角的三角函数值，负整数指数幂和绝对值可以解答本题；
先算括号内的式子，然后计算括号外的除法即可．
本题考查分式的混合运算、实数的运算法，熟练掌握运算法则是解答本题的关键．
 

17.【答案】 

【解析】解：由表格可得，乙校的有人，的有人，
补全条形统计图，如下图．

由条形统计图可得，
甲校数据按照从小到大排列是：、、、、、、、、、、、、、、、、、、、、、、、、、、、、、，
这组数据的中位数，众数；
故答案为：；；
甲校的平均分高于乙校，说明总成绩甲校好于乙校，中位数甲校高于乙校，说明甲校一半以上的学生成绩较好；
为进一步提高两所学校学生的中华文化知识水平，建议在课后多开展中华文化知识活动．
根据表格中的数据可以得到乙校，的和的各有多少人，从而可以将条形统计图补充完整；
根据表格中的数据将甲校的数据按照从小到大排列，即可得到这组数据的中位数和众数；
答案不唯一，理由需包含数据提供的信息；
答案不唯一，理由需支撑推断结论．
本题考查条形统计图、中位数、众数、平均数，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
 

18.【答案】解：矩形的边在轴上，，，
，
反比例函数在第三象限的图象经过点，
，
这个函数的解析式为；
四边形是矩形，
为对角线、的交点，
为的中点，
，．
；
把代入得，，
点在函数的图象上；
由图象可知：不等式的解集是或．

【解析】利用待定系数法求得解析式即可；
根据矩形的性质，求得点的坐标，把点代入反比例函数解析式判定即可；
根据图象即可求得．
本题考查了反比例函数和一次函数的交点，考查了待定系数法求反比例函数的解析式，反比例函数图象上的坐标特征以及函数和不等式的关系．
 

19.【答案】解：答案不唯一，如：方案一适合底部可直接到达；底部不可到达；方案二适合测量底部不可直接到达的物体的高度；在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离；
解：由题意可得：四边形，四边形是矩形，
，，
设．
在中，，，
，
在中，，，
，
，
，
，
，
米，
答：“永泰寺塔”的高度约为米．

【解析】根据题意写出原因即可；
根据矩形的性质得到，，设解直角三角形即可得到结论．
本题考查的是解直角三角形的应用仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．
 

20.【答案】解：如图，为所作；

证明：连接，如图，
，
点在上．
点在上，
圆周角定理，
，
，
．
故答案为：圆周角定理；．

【解析】利用几何语言画出对应的几何图形；
先根据圆周角定理得到，再利用等腰三角形的性质得到，从而得到．
本题考查作图复杂作图，等腰三角形的性质，圆周角等知识，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
 

21.【答案】解：设购买一个甲品牌的篮球为元，则购买一个乙品牌的篮球元，
由题意可得：，
解得，
，
答：购买一个甲品牌的篮球为元，购买一个乙品牌的篮球元；
设购买甲品牌的篮球个，则购买乙品牌的篮球个，
由题意可得：，
解得，
为整数，
，，，，，，，，，，，
即这次学校有种购买方案；
设学校在第二次购买活动中需要资金为元，
，
，
随的增大而减小，
，
当时，取得最小值，此时，
答：学校在第二次购买活动中至少需要资金元．

【解析】根据题意和题目中的数据，可以列出相应的方程组，然后求解即可；
根据题意和题目中的数据，可以写出相应的不等式组，然后求解即可，注意为整数；
根据题意，可以写出所需资金与购进甲种品牌数量的函数关系式，再根据中的结果和一次函数的性质，即可求得学校在第二次购买活动中至少需要多少资金．
本题考查一元一次方程的应用、一元一次不等式组的应用、一次函数的应用，解答本题的关键是明确题意，写出相应的方程和不等式组，写出相应的函数解析式，利用一次函数的性质求最值．
 

22.【答案】解：由题意得：，
解得：，
抛物线的函数表达式为．
．
当时，，
令，得，
解得：或，
当时，在自变量的值满足的情况下的最小值不为；
当二次函数向左平移时，
，且当时，随的增大而增大，
，
当二次函数向右平移时，
，
综上所述，或．

【解析】通过对称轴为直线和代入点列出方程组，求得和的大小，从而得到二次函数的解析式；
先将二次函数的化为顶点式，可知时，二次函数的最小值为，即可知在自变量的值满足的情况下不能取到二次函数的最小值，然后针对平移的方向进行分类讨论．
本题考查了二次函数的对称轴和图象上点的坐标特征，二次函数的性质，第二问的关键是通过分类讨论结合函数的性质得到的取值．
 

23.【答案】解：依据：三角形的中位线平行于第三边并且等于第三边的一半；
依据：直角三角形的两锐角互余．
结论：，理由如下：
如图：

，，
，
，
，
是等腰直角三角形，
，
，
．
证明：连接，如图：

由旋转知，，
，，
≌．
，．
点，，分别是，，的中点，
，分别是，的中位线，
，，
．
是等腰三角形．
又，．
，．
，
，
，
．
，
是等腰直角三角形．
的面积会发生变化，理由如下：
由知，是等腰直角三角形，，
最大，即最大，面积最大，此时点在的延长线上，如图：

，

，
当最小，即最最小，面积最小，此时点在线段上，如图：

，
，
；
面积的最大值为，最小值为．

【解析】利用三角形中位线定理，直角三角形的性质解决问题即可．结论：利用等腰直角三角形的性质以及平行线的性质证明即可；
证明≌推出，再利用三角形的中位线定理，平行线的性质证明即可；
由知，是等腰直角三角形，，可知最大时，面积最大，最小时，面积最小，解得点在的延长线上，最大为，在线段上时，最小为，由此即可解决问题．
本题属于几何变换综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，三角形中位线定理，平行线的性质等知识，解题的关键是正确寻找全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．