



数学必修 第一册2.2 分层随机抽样图片课件ppt
展开那么当总体中的个体有很大差异时,适宜采用什么抽取方法?
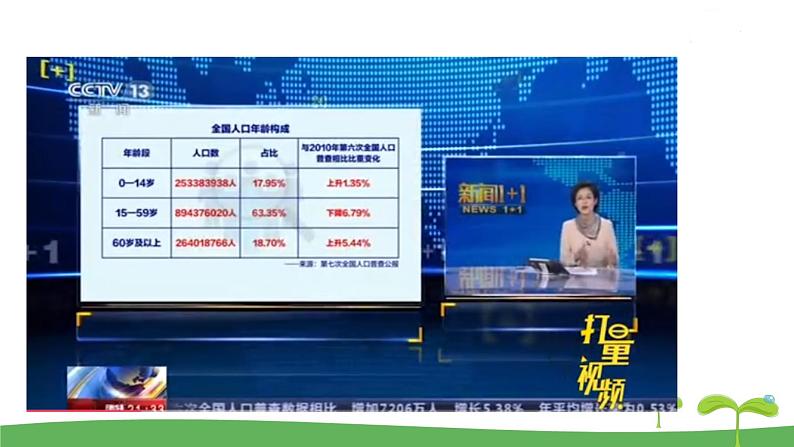
问题1:全国各地的人口和住户的基本情况相同吗?
不同,有很大的差异
问题2:如果用简单随机抽样或系统抽样来抽取,样本具有代表性吗?
不具有代表性
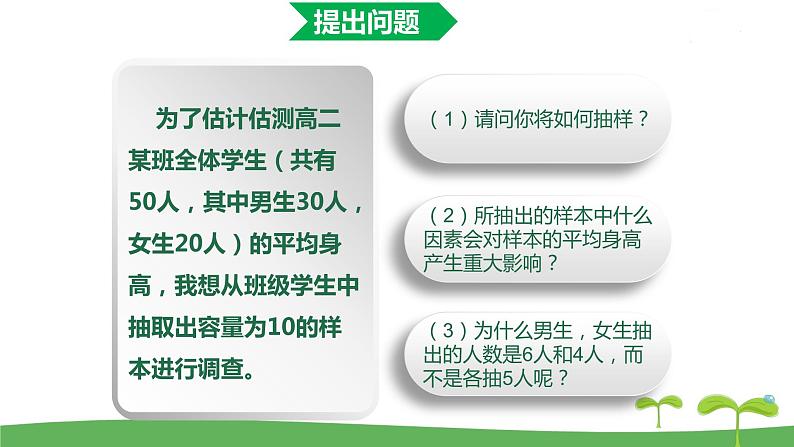
(1)请问你将如何抽样?
(2)所抽出的样本中什么因素会对样本的平均身高产生重大影响?
(3)为什么男生,女生抽出的人数是6人和4人,而不是各抽5人呢?
将总体按其属性特征分成互不交叉的若干类型(有时称作层),然后在每个类型中按照所占比例随机抽取一定的个体,这种抽样方法通常叫作分层随机抽样
(1)将总体按一定的标准分层(分层)(2)计算各层的个体数与总体的个体数的比(定比)(3)按各层个体数与总体的个体数的比确定各层应抽取的样本容量(定量)(4)在每一层进行抽样(抽样)
判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.(1)分层随机抽样适用于总体由差异明显的几部分组成,而层内个体间无明显差异的抽样.( √ )(2)在分层随机抽样中,各层抽取的个体数相等.( × )(3)用分层随机抽样的方法,在分层时,每层的各个个体互不交叉,既不重复,又不遗漏.( √ )(4)在分层随机抽样中,每个个体被抽到的可能性是相等的,与层数及分层无关.( √ )
下列问题中,采用怎样的抽样方法较为合理?(1)从10台冰箱中抽取3台进行质量检查;(2)某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名.为了了解教职工对校务公开方面的意见,拟抽取一个容量为20的样本.
例1.某电视台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如表所示
电视台为进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应怎样进行抽样?
分析:人数多,差异大→分层随机抽样→确定每层抽取的比例→在各层中分别抽取→合在一起得样本
在分层随机抽样的过程中,为了保证每个个体被抽到的可能性是相等的,要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比.
例2. 某学校有在编人员200人,其中行政人员20人,教师140人,后勤人员40人.教育部门为了解学校职工对学校县管校聘改革的意见,要从中抽取20人,试确定用何种方法抽样,并写出抽样过程.
将总体分成互不交叉的几层,按比例分层抽样
总体由差异明显的几部分组成
从总体中逐个不放回抽取
抽样过程中每个个体被抽取的可能性相等
各层抽样时采用简单随机抽样
1.某公司生产三种型号的轿车,产量分别为1200辆、6000辆、和2000辆. 为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车应分别抽取 、 、和 辆.2.某所学校有小学部、初中部和高中部,在校小学生、初中生和高中生之比为5:2:3,且已知初中生有800人.现要从这所学校中抽取一个容量为80的样本以了解他们对某一问题的看法,应采用什么抽样方法?从小学部、初中部及高中部各抽取多少名?总体上看,平均多少名学生中抽取到一名学生?
1.分层抽样的概念、特征及步骤;2.三种抽样方法相互之间的区别与联系.
高中数学北师大版 (2019)必修 第一册2.2 分层随机抽样精品课件ppt: 这是一份高中数学北师大版 (2019)必修 第一册2.2 分层随机抽样精品课件ppt,文件包含北师大版2019数学必修第一册622《分层随机抽样》课件pptx、北师大版2019数学必修第一册622《分层随机抽样》学案docx、北师大版2019数学必修第一册622《分层随机抽样》教案docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
北师大版 (2019)2.2 分层随机抽样优质课课件ppt: 这是一份北师大版 (2019)2.2 分层随机抽样优质课课件ppt,文件包含北师大版高中数学必修第一册622分层随机抽样课件pptx、北师大版高中数学必修第一册622分层随机抽样同步练习含答案docx等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
数学必修 第一册第六章 统计2 抽样的基本方法2.2 分层随机抽样图文课件ppt: 这是一份数学必修 第一册第六章 统计2 抽样的基本方法2.2 分层随机抽样图文课件ppt,共25页。PPT课件主要包含了环节一,情境导入,环节二,分层抽样概念,环节三,分层抽样应用等内容,欢迎下载使用。













