2022年湖北省武汉市洪山区中考数学模拟试卷（附答案）

 中考数学模拟试卷

一、单选题

1． 的相反数是（　　）  

A． B．2 C． D．

2．袋子中装有2个黑球和1个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，下列事件中是必然事件的是（　　） 

A．摸出的2个球中有1个球是白球

B．摸出的2个球中至少有1个球是黑球

C．摸出的2个球都是黑球

D．摸出的2个球都是白球

3．下面是科学防控新冠知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（　　） 

A． B．

C． D．

4．下列几何体是由4个相同的小正方体搭成的，其中，主视图、左视图、俯视图都相同的是（　　）  

A． B．

C． D．

5．计算（﹣2x2）4的结果是（　　） 

A．8x6 B．﹣8x8 C．﹣16x8 D．16x8

6．布袋中装有除颜色外没有其他区别的1个红球和2个白球，搅匀后从中摸出一个球，放回搅匀，再摸出第二个球，两次都摸出白球的概率是（　　）

A． B． C． D．

7．已知反比例函数 ，当|y|≥3时，x的取值范围是（　　） 

A．x≥2或x≤﹣2 B．﹣2≤x≤2

C．0＜x≤2或x≤﹣2 D．﹣2≤x＜0或0＜x≤2

8．如图1，点F从菱形ABCD的顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B，△FBC的面积y（cm2）随时间x（s）变化的关系图象，则a的值为（　　）

A． B．2 C． D．2

9．如图，AB和CD是⊙O的两条互相垂直的弦，若AD＝4，BC＝2，则阴影部分的面积是（　　）

A．2π﹣1 B． π﹣4 C．5π﹣4 D．5π﹣8

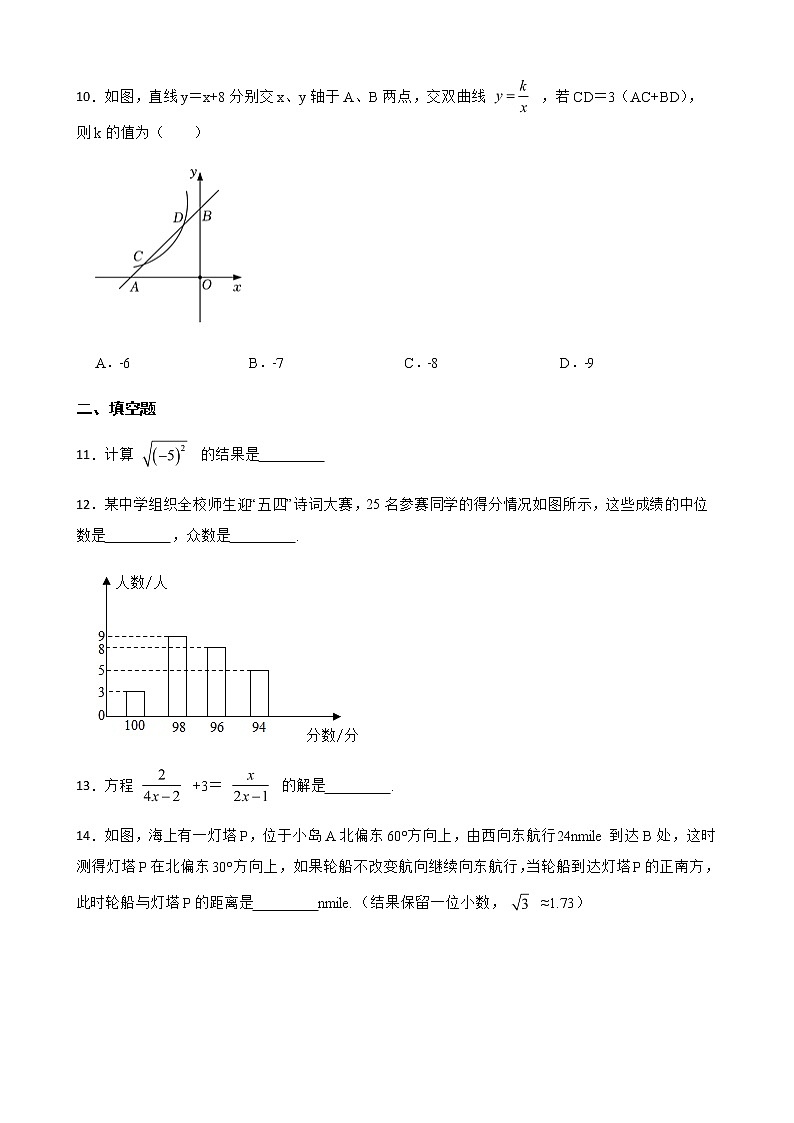
10．如图，直线y＝x+8分别交x、y轴于A、B两点，交双曲线 ，若CD＝3（AC+BD），则k的值为（　　） 

A．﹣6 B．﹣7 C．﹣8 D．﹣9

二、填空题

11．计算 的结果是　     　

12．某中学组织全校师生迎“五四”诗词大赛，25名参赛同学的得分情况如图所示，这些成绩的中位数是　     　，众数是　     　.

13．方程 +3＝ 的解是　     　.

14．如图，海上有一灯塔P，位于小岛A北偏东60°方向上，由西向东航行24nmile到达B处，这时测得灯塔P在北偏东30°方向上，如果轮船不改变航向继续向东航行，当轮船到达灯塔P的正南方，此时轮船与灯塔P的距离是　     　nmile.（结果保留一位小数， ≈1.73） 

15．抛物线y＝ax2+bx+c（a，b，c是常数，a＜0）的顶点坐标为（1，m），其中m＞0.下列四个结论：

①ab＜0；

②c＞0；

③关于x的一元二次方程ax2﹣bx+c＝m+1无实数解；

④点P1（n，y1），P2（3﹣2n，y2）在抛物线上，若n＜1，则y1＜y2.

其中正确的结论是　     　（填写序号）.

16．如图，在△ABD中，∠ADB＝90°，AB＝8，C是AB中点，E是BD中点，将点E绕B点顺时针旋转90°为点F，则CF的最小值为 　     　.

三、解答题

17．不等式组 请按下列步骤完成解答：

（1）解不等式①，得　     　；

（2）解不等式②，得　     　；

（3）把不等式①和②的解集在数轴上表示出来；

（4）原不等式组的解集为　          　

18．已知：如图，D，E，F分别是AB，AC，BC上的点，DE∥BC，∠ADE=∠EFC，求证：∠1=∠2.

19．某校组织学生书法比赛，对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析，并绘制扇形统计图和条形统计图如下：

（1）直接写出这次抽取的样本的容量为　     　；

（2）请在图2中把条形统计图补充完整.

（3）已知该校这次活动共收到参赛作品800份，请你估计参赛作品达到B级以上（即A级和B级）有多少份？

20．如图，△ABC的顶点均为格点，AC与网格线交于点D.仅用无刻度尺的直尺在网格中画图，画图过程用虚线表示，画图结果用实线表示.

（1）如图1，画出△ABC的角平分线CE；

（2）如图1，平移AB至DN，使点A的对应点为点D；

（3）如图2，在AB上找一点G，使DG+CG最小；

（4）如图3，AB与网格线交于点E，过点E作EQ⊥AC于Q.

21．如图1，已知AB是⊙O的直径，C，D为⊙O上的点，BD平分∠ABC，过D作DP⊥BC交BC的延长线于点P.

（1）求证：DP是⊙O的切线.

（2）如图2，若E是OB的中点，EF⊥OB交直线DP于点F，EF= ，tan∠ABD＝ ，求⊙O的半径.

22．某公司投入研发费用120万元（120万元只计入第一年成本），成功研发出一种产品，产品正式投产后，生产成本为8元/件.经试销发现年销售量y（万件）与售价x（元/件）有如表对应关系.

（1）直接写出y关于x的函数关系式：　          　.

（2）若物价部门规定每件商品的利润率不得超过150%，当第一年的产品的售价x为多少时，年利润W最大，其最大值是多少？

（3）为了提高利润，第二年该公司将第一年的最大利润再次投入研发（此费用计入第二年成本），使产品的生产成本降为5元/件，但规定第二年产品的售价涨幅不能超过第一年售价的20%，在年销售量y（万件）与售价x（元/件）的函数关系不变的情况下，若公司要求第二年的利润不低于166万元，求该公司第二年售价x（元/件）应满足的条件.

23．如图1，在四边形ABCD中，AB∥CD，AC、BD相交于点P， . 

（1）求证：∠BAC＝∠CBD；

（2）如图2，E，F分别为边AD、BC上的点，PE DC，  ， 

①求证：∠PFC＝∠CPD；

②若BP＝2，PD＝1，锐角∠BCD的正弦值为   ，直接写出BF的长.

24．已知抛物线y＝ . 

（1）如图1，当c＝﹣6时，抛物线分别交x轴于A，B，交y轴于点C.

①直接写出直线CB的解析式；

②点P在直线BC下方抛物线上，作PD y轴，交线段BC于点D，作PE x轴，交抛物线于另一点E，若PE＝PD，求点P的坐标；

（2）如图2，若抛物线与x轴有唯一公共点F，直线l：y＝kx+b（k＞0，b＞0）与抛物线交于M，N两点（点N在点M右边），直线MG⊥x轴，交直线NF于点G，且点G的纵坐标为-3，求证：直线l过定点.

答案解析部分

1．【答案】B

2．【答案】B

3．【答案】A

4．【答案】A

5．【答案】D

6．【答案】A

7．【答案】D

8．【答案】C

9．【答案】B

10．【答案】B

11．【答案】5

12．【答案】96分；98分

13．【答案】

14．【答案】20.8

15．【答案】①③

16．【答案】

17．【答案】（1）

（2）

（3）

（4） .

18．【答案】证明：∵DE∥BC，

∴∠ADE＝∠ABC.

∵∠ADE＝∠EFC，

∴∠ABC＝∠EFC.

∴AB∥EF.

∴∠1＝∠2.

19．【答案】（1）120

（2）解：由C级在扇形图中所占比例为30%，可得C级人数为：120×30%＝36人，

∴D级人数为：120﹣36﹣24﹣48＝12人，

条形图如图所示：

（3）解：由题意得A级和B级作品在样本中所占比例为：（24+48）÷120×100%＝60%，

∵800×60%＝480

∴该校这次活动共收到参赛作品800份，参赛作品达到B级以上有480份.

20．【答案】（1）解：如图1中，线段CE即为所求作.

（2）解：如图1中，线段DN即为所求作.

（3）解：如图2中，点G即为所求作.

（4）解：如图3中，直线EQ即为所求作.

21．【答案】（1）证明：连接OD，

∵DP⊥BC，

∴∠P＝90°，

∵OB＝OD，

∴∠OBD＝∠ODB，

∵BD平分∠ABC，

∴∠OBD＝∠DBC，

∴∠ODB＝∠DBC，

∴OD∥BC，

∴∠ODP+∠P＝180°，

∴∠ODP＝180°﹣∠P＝90°，

∵OD是圆O的半径，

∴DP是⊙O的切线；

（2）解：设EF与BD交于点G，连接OF，⊙O的半径为 ，

∵E是OB的中点，

∴OE＝BE＝ OB＝ r，

∵EF⊥OB，

∴∠BEF＝∠OEF＝90°，

∵tan∠ABD＝ ，

∴ ＝ ，

∴EG＝ BE＝ r，

∵EF＝ ，

∴GF＝EF﹣EG＝ ﹣ r，

∵∠BEG＝∠ODF＝90°，

∴∠ABD+∠BGE＝90°，∠ODB+∠FDB＝90°，

∵∠OBD＝∠ODB，

∴∠BGE＝∠FDB，

∵∠BGE＝∠DGF，

∴∠DGF＝∠FDB，

∴FD＝FG＝ ﹣ r，

在Rt△ODF中，OF2＝OD2+DF2＝r2+（ ﹣ r）2，

在Rt△OEF中，OF2＝OE2+EF2＝（ r）2+（ ）2，

∴r2+（ ﹣ r）2＝（ r）2+（ ）2，

∴r＝4或r＝0（舍去），

∴⊙O的半径为4.

22．【答案】（1）y＝﹣x+40

（2）解：∵每件商品的利润率不得超过150%，

∴x≤8（1+150%），即x≤20，

由题意得：

W=（x-8）（-x+40）-120

=-x2+48x-440

=-（x-24）2+136，

∵-1＜0，x≤20在对称轴直线x=24左侧，W随x的增大而增大，

∴当x=20时，年利润W最大，Wmax=-（20-24）2+136=120，

∴售价x为20元时，年利润W最大，其最大值是120万元；

（3）解：∵第二年产品的售价涨幅不能超过第一年售价的20%，

∴第二年产品的售价x≤20×（1+20%），即x≤24，

根据题意得：（x-5）（-x+40）-120≥166，

解得18≤x≤27，

∴该公司第二年售价x（元/件）应满足的条件是18≤x≤24.

23．【答案】（1）证明：∵ ， 

∴ ，

又∵ ，

∴ ，

∴ ，

又∵ ，

∴ ，

∴ ；

（2）解：①如图，延长EP交BC于M ， 

∵ ，

∴ ，   ，

又∵ ，

∴ ，

∴ ，即   ，

∵ ，

∴ 中，   ，

∴ ，

又∵ ，

∴ ，

∴ ，

由（1）可得   ，

∴ ，

∴ ；

②

24．【答案】（1）解：①y＝x﹣6

②

∵抛物线为 ，

∴对称轴为直线 ，

设点P的坐标为（t， ），则D（t，t﹣6）

∴PD＝（t﹣6）﹣（ ）＝ ，

∵PE∥x轴，

∴点P与点E关于抛物线对称轴直线x＝2对称，

∴E（4﹣t， ），

∴PE＝|4﹣t﹣t|＝|4﹣2t|，

∵PE＝PD，

∴ ＝|4﹣2t|，

当t≥2时， ＝2t﹣4，

整理得

解得：t＝4或t＝﹣2（舍去），

∴

∴P（6，﹣6），

当t＜2时， ＝4﹣2t，

整理得

解得：

（舍弃）， ，

∴P（5﹣ ，5﹣3 ），

综上，点P的坐标为（6，﹣6）或（5﹣ ，5﹣3 ）；

（2）证明：∵抛物线y＝ 与x轴有唯一公共点F， 

∴Δ＝（﹣2）2﹣4× ＝0，

解得：c＝2，

∴ ，

此时，F（2，0）

如图2，过点N作NT⊥x轴于点T，

设点M（m， ），N（n， ），G（m，-3）

则 ，

∴m、n是方程 x2+（﹣2﹣k）x+2﹣b＝0的两个解，

∴m+n＝2k+4，mn＝4﹣2b，

∵∠SFG＝∠NFT，

∴tan∠SFG＝tan∠NFT，即 ，

∴ ，

∴（n﹣2）（2﹣m）＝6，

∴2（m+n）﹣mn＝10，

∴2（2k+4）﹣（4﹣2b）＝10，

∴b＝3﹣2k，

∴直线l解析式为y＝kx+3﹣2k＝k（x﹣2）+3，

∴当x＝2时，y＝3，

∴直线l经过定点（2，3）.