
2022年江苏省淮安市洪泽区中考二模数学试题(word版含答案)
展开洪泽区2021-2022学年度第二学期九年级学业水平调研测试(二)
数学试题
(考试时间:120分钟 卷面满分:150分)
友情提醒:请将本卷答案填写在答题纸上.
一、选择题(本大题共8小题,每小题3分,共24分)
1.的相反数是( )
A. B.2 C. D.
2.随着科学技术的不断提高,5G网络已经成为新时代的“宠儿”,预计到2025年,中国5G用户将超过460000000人.将数据460000000用科学记数法表示是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.某市四月份连续7天的最高气温依次是:18,15,16,15,16,18,19(单位:),则这组数据的中位数是( )
A.16 B.17 C.18 D.19
5.下列图形中,能围成正方体的是( )
A. B. C. D.
6.如图,在中,,将绕点A顺时针旋转得到,则的度数是( )
A. B. C. D.
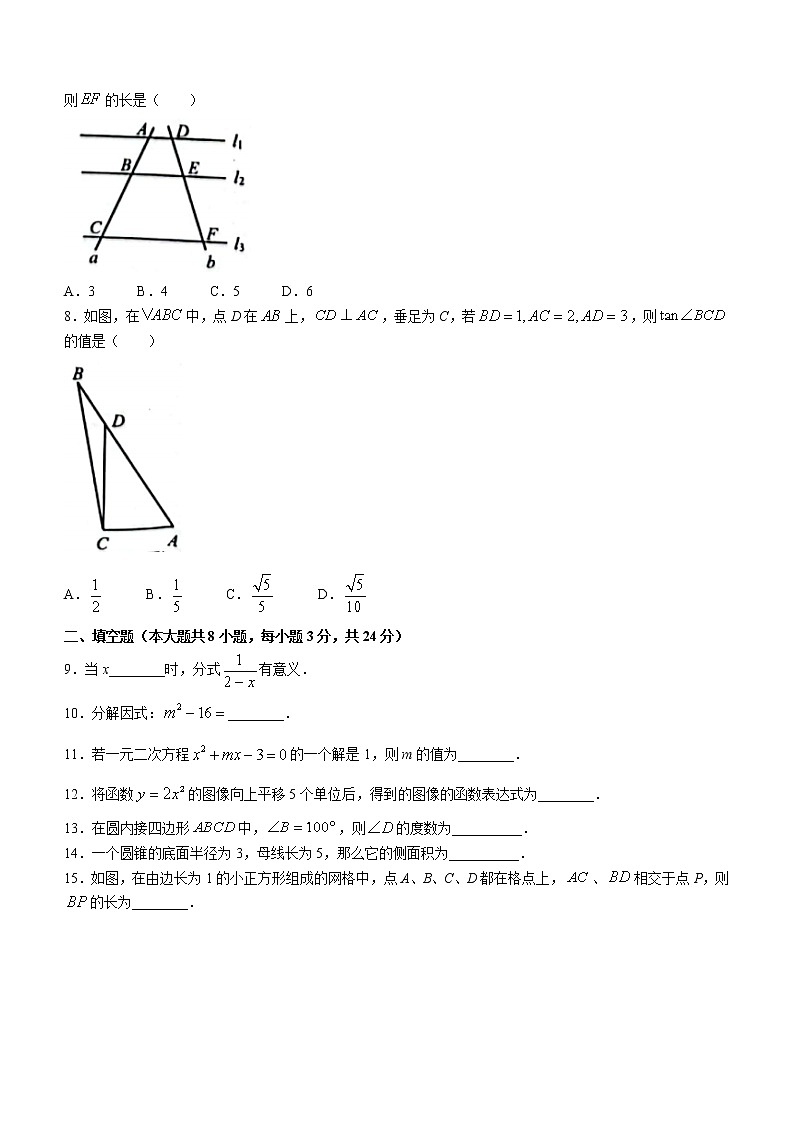
7.如图,,直线a、b与分别交于点A、B、C和点D、E、F,若,,则的长是( )
A.3 B.4 C.5 D.6
8.如图,在中,点D在上,,垂足为C,若,则的值是( )
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
9.当x________时,分式有意义.
10.分解因式:________.
11.若一元二次方程的一个解是1,则m的值为________.
12.将函数的图像向上平移5个单位后,得到的图像的函数表达式为________.
13.在圆内接四边形中,,则的度数为__________.
14.一个圆锥的底面半径为3,母线长为5,那么它的侧面积为__________.
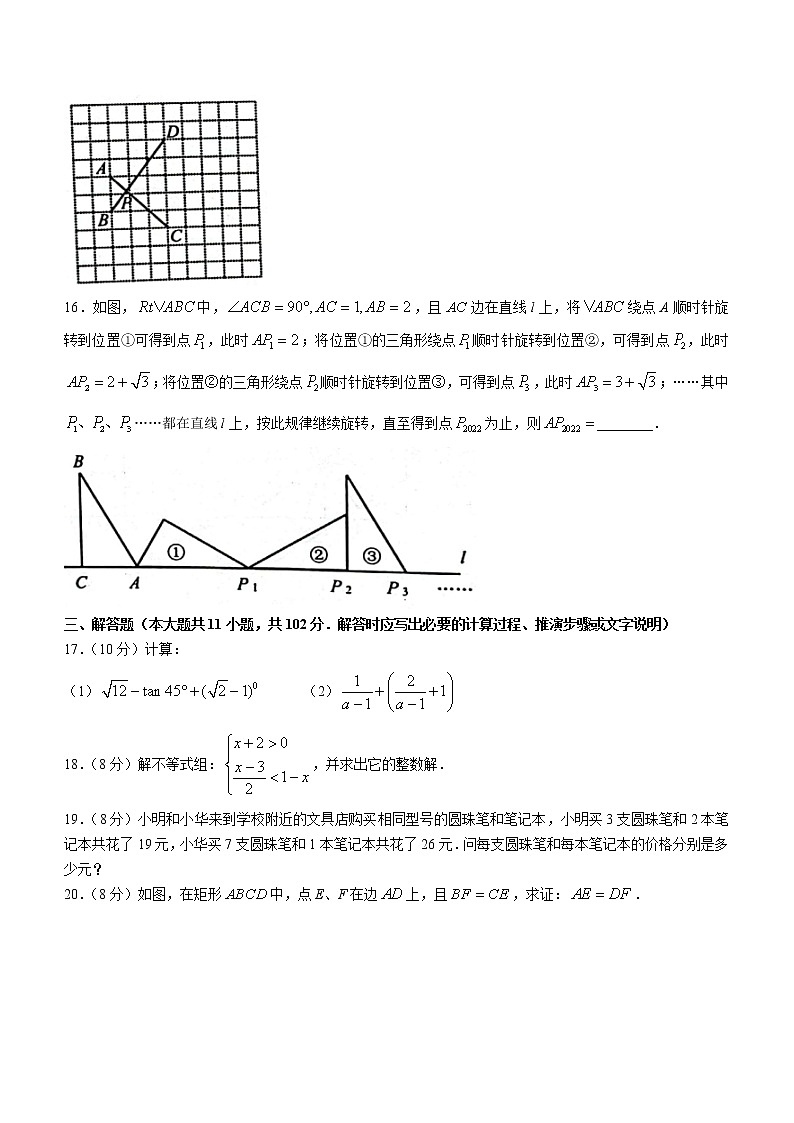
15.如图,在由边长为1的小正方形组成的网格中,点A、B、C、D都在格点上,、相交于点P,则的长为________.
16.如图,中,,且边在直线l上,将绕点A顺时针旋转到位置①可得到点,此时;将位置①的三角形绕点顺时针旋转到位置②,可得到点,此时;将位置②的三角形绕点顺时针旋转到位置③,可得到点,此时;……其中……都在直线l上,按此规律继续旋转,直至得到点为止,则________.
三、解答题(本大题共11小题,共102分.解答时应写出必要的计算过程、推演步骤或文字说明)
17.(10分)计算:
(1) (2)
18.(8分)解不等式组:,并求出它的整数解.
19.(8分)小明和小华来到学校附近的文具店购买相同型号的圆珠笔和笔记本,小明买3支圆珠笔和2本笔记本共花了19元,小华买7支圆珠笔和1本笔记本共花了26元.问每支圆珠笔和每本笔记本的价格分别是多少元?
20.(8分)如图,在矩形中,点E、F在边上,且,求证:.
21.(9分)为了了解某区学生课外阅读情况,该区教育部门抽取了部分学生统计了他们在2021年一年内阅读课外书的册数,数据整理成如下尚不完整的统计表和统计图.
某区学生阅读课外书册数情况统计表
组别 | 阅读课外书x(册) | 人数 |
A | 2 | |
B | 10 | |
C |
| |
D | 14 | |
E | 4 |
(1)一共抽取了________名学生;
(2)补全条形统计图,在扇形统计图中,表示C组占比的扇形圆心角度数为__________;
(3)该区共有300名学生,请估计该区阅读课外书超过300册学生有多少名?
22.(8分)一个不透明的布袋里装有2个白球、1个黑球,它们除颜色外大小质地都相同.
(1)从布袋中随机摸出一个球,摸出是黑球的概率是________;
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
23.(8分)某校航模小组打算制作模型飞机,设计了如图所示的模型飞机机翼图纸.图纸中,均与水平方向垂直,机翼前缘、机翼后缘与水平方向形成的夹角度数分别为、,,点D到直线的距离为.求机翼外缘的长度(参考数据:).
24.(10分)如图1,小明妈妈购物结束后,准备从超市(点A)出发,沿步行回家(点B),由于买的东西多,妈妈就让正准备出门散步的小明来接.小明接到妈妈的“指令”后,与妈妈同时出发,沿“方向赶过去.接过妈妈的物品后立即沿原路返回,小明到家后再过分钟,妈妈也到家了.已知两人的速度均保持不变,设妈妈步行时两人之间的距离为,从妈妈从超市出发回到家,y与x的函数关系如图2所示,
根据图像,解决下列问题:
(1)小明与妈妈的速度分别为多少?
(2)图2中点C的实际意义为________;
(3)求出所在直线函数表达式.
25.(10分)如图,在中,,以为直径作,交于点D,是的切线.
(1)求证:;
(2)若的面积为40,求的半径.
26.(本题第(1)问9分,第(2)问2分,共11分)如图1,将三角形纸片()进行以下操作:第一步:折叠三角形纸片使点C与点A重合,得到折痕,然后展开铺平;第二步:将绕点D顺时针方向旋转得到,点E、C的对应点分别是点F、G,直线与边交于点M(点M不与点A重合),与边交于点N.
(1)已知.
①在绕点D旋转的过程中,试判与的数量关系,并证明你的结论;
②如图2,在绕点D旋转的过程中,当直线经过点B时,求的长;
(2)如图3,若直角三角形纸片的两直角边,在点G从点C开始顺时针旋转的过程中,设与的重叠部分的面积为S,则S的最小值为________.
27.(12分)如图1,抛物线与x轴正半轴交于点A,该抛物线的项点为M,直线经过点A,与y轴交于点B.
(1)__________;
(2)如图2,将直线向下平移,使它经过点M,且与x轴负半轴交于点C,取点,连接,求的度数;
(3)点E是线段上一动点,点F是线段上一动点,线段的延长线与线段交于点G.当时,是否存在点E,使得?若存在,求出点E的坐标;若不存在,请说明理由.
洪泽区2021-2022学年度第二学期九年级学业水平调研测试(二)
数学试题参考答案
一、选择(每小题3分,共24分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | C | D | A | C | A | D | D |
二、填空(每小题3分,共24分)
9. 10. 11.2 12. 13.80 14. 15. 16.或
三、解答(共102分)
17.(1)原式
(2)原式
18.由不等式得:
由不等式得:
∴此不等式组的解集为:
∴此不等式组的整数解为:、0、1.
19.设每支圆珠笔的价格为x元,每木笔记木的价格为y元
由题意:解之得:
答:每支圆珠笔的价格为3元,每本笔记本的价格为5元
20.∵四边形是矩形
∴,
在和中,
∴
∴
∴,好
21.(1)50
(2)20图略,
(3)(名)
答:估计捐款金额超过300元的党员有1080名
22.(1)
(2)列表:
| 白 | 白 | 黑 |
白 |
| (白,白) | (黑,白) |
白 | (白,白) |
| (黑,白) |
黑 | (白,黑) | (白,黑) |
|
∵一共有6种可能出现的结果,它们是等可能的,其中两次摸到的球都是白球有2种.
∴两次摸到的球都是白球的概率为.
23.过点A作的垂线,交的延长线于点E.
过点D作的垂线,交的延长线于点F.
在四边形中,
∵,
∴,在此处键入公式,
又,
∴四边形是矩形
∴.
在中,,
∴.
在中,.
∴.
∴.
24.(1),
,
答:小明与妈妈的速度分别为和.
(2)图2中C的实际意义为:小明与妈妈经过10分钟在距家1000米(或距超市600米)处相遇;
(3)小明返回到家时与妈妈相距,则,
妈妈从超市到家共用分钟,则,
设所在直线函数表达式,
解得:
∴所在直线函数表达式.
25.(1)连接.
∵是的切线,∴.
∴.
∵,∴.
∵,∴.
∴.
∴.
∴,∴.
其它证法酌情给分
(2)连接.
∵是的直径,∴,∴.
又∵,∴D是的中点.
∴.
又∵,且,∴.
∴的半径为5.
26.(1)①
∵折叠三角形纸片使点C与点A重合,得到折痕,
∴.∴.
连接,根据旋转性质可知:
.
又∵
∴
∴.
②∵翻折,∴.
∵,∴,
∴,∴,∴.
∴,∴
设,则,在中,
解得,即
(2).
▲第(2)小题简解:
当绕点D顺时针旋转时,所得的与的重叠部分的面积S最小.
理由如下:
若绕点D顺时针旋转后,所得的三角形为.
设、、、交分别于点M、、P、.
由题意可知,.
由于.
同理,.
①如图1,若旋转的角度等于,
则.
由题意知,是等腰三角形,且直线是其对称轴,
于是,作关于直线的对称线段.连接,作的平分线,交于点Q.
由题意知,,
因而,所以.
在、上分别取点、,使,连接、.
易得.
因为,所以,
同理.
因而,从而.
②如图2,若旋转的角度等于,
则.
在、上分别取点、,
使,,
连接、.易得.
因为,所以.
同理.
因而,从而.
综上所述,当时,四边形的面积最小.
如图3,作,垂足为H,则(设等于),,
,
由,得.解得.
进而.
所以.
建议在评讲完第(3)小题后,可以把第(4)小题改编为如下题目,供学有余力的学生继续思考:
(4)在绕点D顺时针旋转的过程中,设与的重叠部分的面积为S,则S的最小值为__________.
27.(1)3
(2)由配方得,∴.
∵由平移所得,∴可设所对应的函数表达式为,
将代入可得所对应的函数表达式为,∴,∴.
连接,作轴,则,
又∵,∴.∵,∴,∴.
在中,,
∴,又∵,∴,
∴.
另解:过点D作,垂足为E,由面积法可以求得,由勾股定理可得,所以,所以.
(3)
▲第(3)小题简解:
作轴,垂足为H,作点F关于直线的对称点P,连接,则.
因为,
所以.因而.设,又,
则.
在中,由勾股定理,得,解.
从而,进而.
作轴,垂足为Q,可得.从而,即.
解得.进而.
由,得.解得.
此时.
因而.
另解:首先构造符合条件的图形:在线段上取点E,作垂直平分线交于P.则,若令,则,作于H,点P关于对称点即为点F,由知,于是,则如图即为符合条件的图形,过点G作,垂足为Q,则,从而,若有,则,令,则由,得,而平分.
所以,所以,于是,,点E在直线上,
所以点E的纵坐标为,
解得,此时,因而.
建议在评讲第(3)小题时,先从“”变化入手,可有多种解法.
另解:令,在内作,则,且,
由勾股定理可得,所以,
所以,所以
过点E作,垂足为H,过点G作,垂足为Q,则,从而,
若有,则,令,则由,得,而平分,
所以,所以,于是,,点E在直线上,所以点E的纵坐标为,
解得,此时,
因而.
2023年江苏省淮安市洪泽区中考二模数学模拟试题: 这是一份2023年江苏省淮安市洪泽区中考二模数学模拟试题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年江苏省淮安市洪泽区中考一模数学试题: 这是一份2023年江苏省淮安市洪泽区中考一模数学试题,共6页。
2023年江苏省淮安市洪泽区中考数学一模试卷(含解析): 这是一份2023年江苏省淮安市洪泽区中考数学一模试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












