2022年湖北省随州市高新区九年级下学期5月联考数学试题(word版无答案)

这是一份2022年湖北省随州市高新区九年级下学期5月联考数学试题(word版无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．的绝对值等于（ ）
A．2022 B． C． D．
2．解决全人类温饱问题是“世界杂交水稻之父”袁隆平的毕生追求，2021年中国早稻总产量达到28020000吨，是世界粮食第一大国，将28020000用科学记数法表示为（ ）
A． B． C． D．
3．如图是一个机器的零件，则下列说法正确的是（ ）
A．主视图与左视图相同 B．主视图与俯视图相同
C．左视图与俯视图相同 D．主视图，左视图与俯视图均不相同
4．直线，其中，，∠3为（ ）
A． B． C． D．
5．下列运算正确的是（ ）
A． B． C． D．
6．在我校“英语课本剧”表演比赛中，初二年级的10名学生参赛成绩统计如图所示，对于这10名学生的参事成绩，下列说法中正确的是（ ）
A．众数是90 B．平均数是88 C．中位数是85 D．方差是6
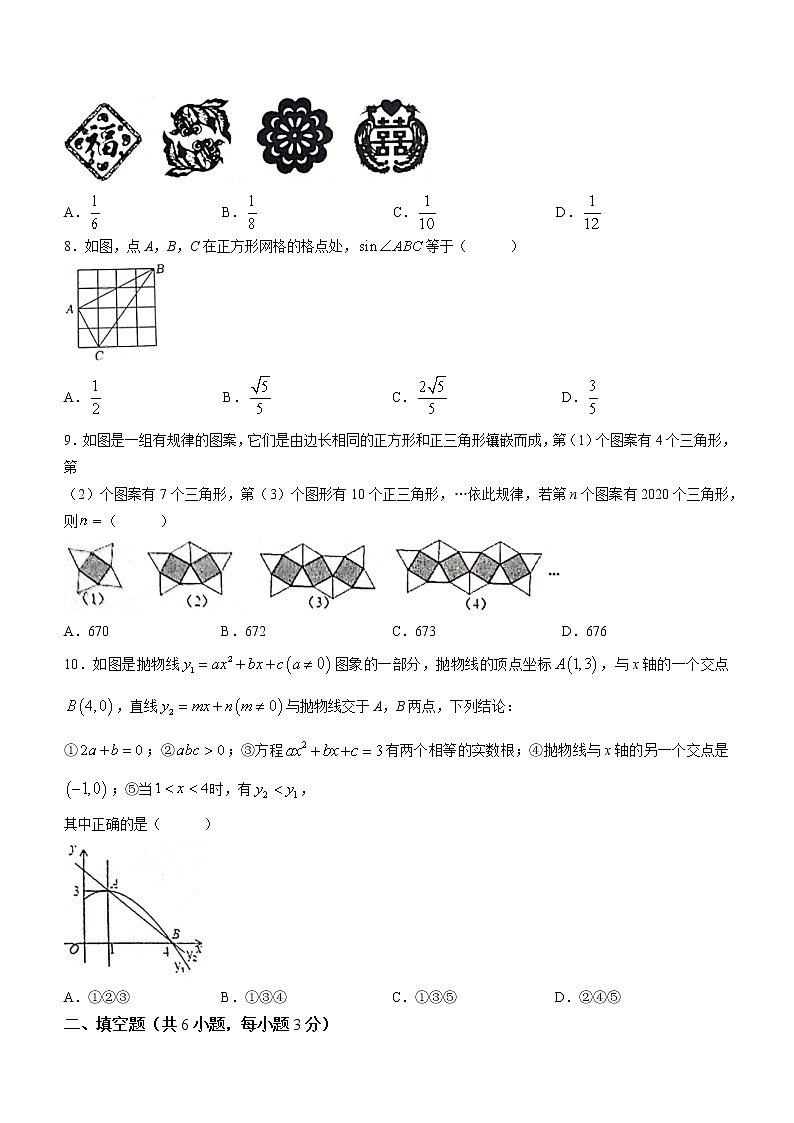
7．剪纸艺术是第一批国家级非物质文化遗产，有4张剪纸卡片的图案如图所示，从这4张卡片中随机抽取两张，则这两张卡片都是中心对称图形的概率是（ ）
A． B． C． D．
8．如图，点A，B，C在正方形网格的格点处，等于（ ）
A． B． C． D．
9．如图是一组有规律的图案，它们是由边长相同的正方形和正三角形镶嵌而成，第（1）个图案有4个三角形，第
（2）个图案有7个三角形，第（3）个图形有10个正三角形，…依此规律，若第n个图案有2020个三角形，则（ ）
A．670 B．672 C．673 D．676
10．如图是抛物线图象的一部分，抛物线的顶点坐标，与x轴的一个交点，直线与抛物线交于A，B两点，下列结论：
①；②；③方程有两个相等的实数根；④抛物线与x轴的另一个交点是；⑤当时，有，
其中正确的是（ ）
A．①②③ B．①③④ C．①③⑤ D．②④⑤
二、填空题（共6小题，每小题3分）
11．计算的结果是 ．
12．如图，在菱形ABCD中，，过A，B，C三点的圆交AD的延长线于点E，连结BE，A日则 度．
13．关于x的一元二次方程的一个根是0，则另一个根是 ．
14．如图，在Rt△ABC中，，，将Rt△ABC绕点A旋转得到，且点C落在AB上，则的度数为 °．
15．下面是一组有规律的算式，根据其中规律，第n个算式为： ．
：第1个算式
：第2个算式
：第3个算式
：第4个算式
……
16如图，正方形ABCD中，，点M是边AB的中点，连接DM，DM与AC交于点P．点B在DC上，点F在DP上，且，若，则DP的长为 ；则 。
三、解答题（共8小题）
17．（本题5分）
先化简，再求值：，其中．
18．（本题7分）
如图，在中，F是CD的中点，延长AB到点E，使，连结BF，CE．
（1）求证：四边形BECF是平行四边形：
（2）若，，，求CE的长．
19．（本题9分）
某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球，学生可以根据自己的爱好选修其中1门，某班班主任对全班同学的选课情况进行了调查统计，制成了两幅不完整的统计图；
（1）请你求出该班的总人数，并补全条形图（注：在所补小矩形上方标出人数）；
（2）在扇形统计图中，“篮球”所在扇形的圆心角度数为 度；
（3）在该班团支部4人中，有1人选修排球，2人选修羽毛球，1人选修乒乓球，如果该班班主任要从他们4人中任选2人作为学生会候选人，那么选出的两人中恰好有1人选修排球、1人
20．（本题9分）
如图，一次函数的图象与反比例函数在第一象限的图象交于和B两点，与x轴交于点C．
（1） ， ；
（2）当时，请结合图象直接写出x的取值范围；
（3）连结OA、OB，求△OAB的面积．
21．（本题9分）
如图，AB是⊙O的弦，过AB的中点E作，垂足为C，过点B作直线BD交CE的延长线于点D，使得．
（1）判断BD与⊙O的位置关系，并说明理由
（2）若，，
①求△BDE的BE边上的高
②求的值．
22．（本题10分）
某商店销售一种商品，经市场调查发现：在实际销售中，该商品的月销售量
y（件）是售价x（元/件）的一次函数，其售价x（元/件）、月销售量y（件）、月销售利润w（元）的部分对应价如表：
注：月销售利润＝月销售量×（售价－进价）
（1）求y关于x的函数表达式；
（2）当该商品的售价是多少元时，月销售利润最大？并求出最大利润；
（3）现公司决定每销售1件商品就捐赠m元利润（）给“精准扶贫”对象，要求：在售价不超过52元时。每天扣除捐赠后的日销售利润随售价x的增大而增大，求m的取值范围
23．（本题11分）
已知点O是线段AB的中点，点P是直线l上的任意一点，分别过点A和点B作直线l的垂线，垂足分别为点C和点D．我们定义垂足与中点之间的距离为“足中距”．
（1）【猜想验证】如图1，当点P与点OC重合时，请你猜想、验证后直接写出“足中距”OC和OD的数量关系是 ．
（2）【探究证明】如图2，当点P是线段AB上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明：若不成立，请说明理由．
（3）【拓展延伸】如图3，①当点P是线段BA延长线上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明：若不成立，请说明理由．
②若，请直接写出线段AC、BD、OC之间的数量关系．
24．（本题12分）
如图，已知二次函数经过A，B两点轴于点C．且）点，，．
（1）求抛物线的解析式；
（2）点E是线段AB上一动点（不与A，B重合），过点E作x轴的垂线，交抛物线于点F，当线段EF的长度最大时，求点E的坐标及；
（3）点P是抛物线对称轴上的一个动点，是否存在这样的P点，使△ABP成为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．售价x（元/件）
40
45
月销售量y（件）
300
250
月销售利润w（元）
3000
3750