【解析版】狮城中学2022年七年级上第二次月考数学试卷

这是一份【解析版】狮城中学2022年七年级上第二次月考数学试卷，共13页。试卷主要包含了选择题，填空题，解答题，综合应用题等内容，欢迎下载使用。
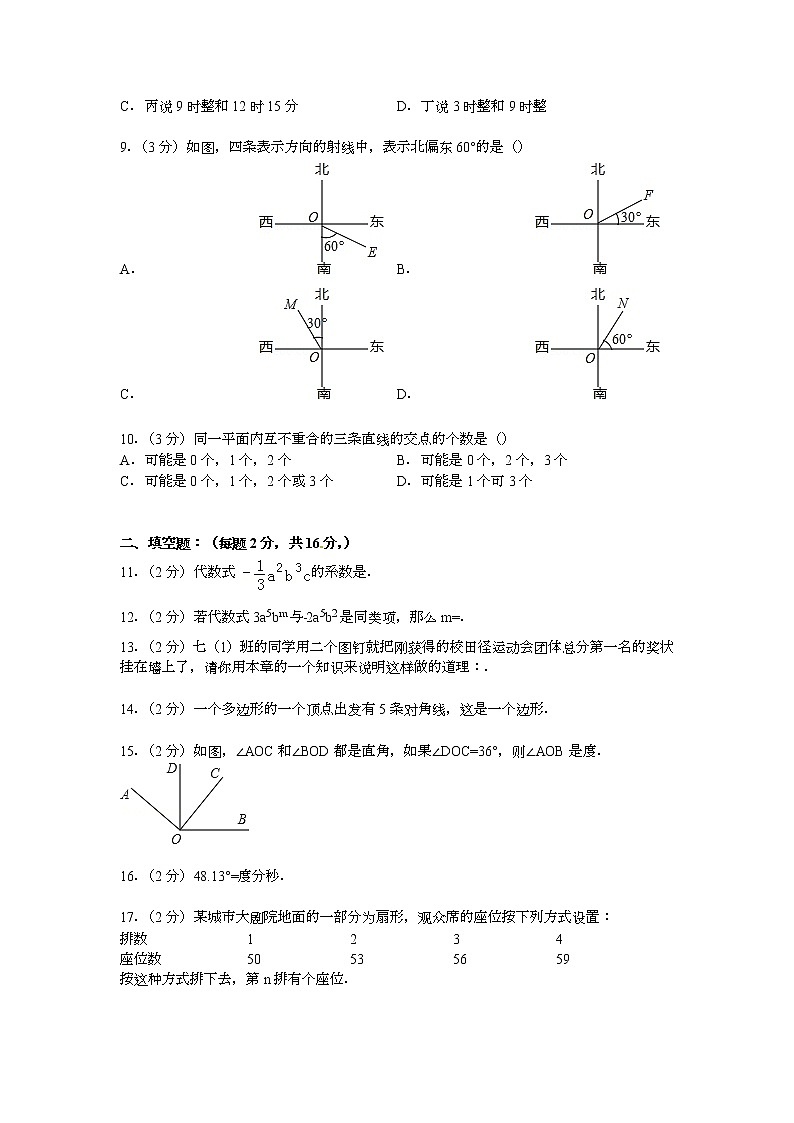
 广东省佛山市狮城中学2022学年七年级上学期第二次月考数学试卷 一、选择题：（每题3分，共30分）1．（3分）﹣的倒数是（） A． ﹣2 B．  C． 2 D． ﹣2．（3分）下列语句中，正确的是（） A． 直线比射线长 B． 射线比线段长 C． 无数条直线不可能相交于一点 D． 两条直线相交，只有一个交点 3．（3分）下列方程中是一元一次方程的是（） A． =7 B． y2﹣y=1 C． 2x﹣3y=1 D． ﹣3+x=1﹣x 4．（3分）下列各题运算正确的是（） A． 3x+3y=6xy B． x+x=x2 C． ﹣9y2+16y2=7 D． 9a2b﹣9a2b=0 5．（3分）若|a|=2，则a=（） A． 2 B． ﹣2 C． 2或﹣2 D． 以上答案都不对 6．（3分）下列方程中，以x=2为解的方程是（） A． x+2=0 B． 2x﹣1=0 C． 2x+4=6+3x D． 2x﹣4=6﹣3x 7．（3分）下列变形错误的是（） A． 由x+7=5，得x+7﹣7=5﹣7 B． 由3x﹣2=2x+1，得x=3 C． 由4﹣3x=4x﹣3，得4+3=4x+3x D． 由﹣2x=3，得x=﹣． 8．（3分）甲、乙、丙、丁四个学生判断时钟的分针与时针互相垂直时，他们每个人都说了两个时间，说对的是（） A． 甲说3点时和3点30分 B． 乙说6点15分和6点45分 C． 丙说9时整和12时15分 D． 丁说3时整和9时整 9．（3分）如图，四条表示方向的射线中，表示北偏东60°的是（） A．  B．  C．  D．  10．（3分）同一平面内互不重合的三条直线的交点的个数是（） A． 可能是0个，1个，2个 B． 可能是0个，2个，3个 C． 可能是0个，1个，2个或3个 D． 可能是1个可3个  二、填空题：（每题2分，共16分，）11．（2分）代数式的系数是．12．（2分）若代数式3a5bm与﹣2a5b2是同类项，那么m=．13．（2分）七（1）班的同学用二个图钉就把刚获得的校田径运动会团体总分第一名的奖状挂在墙上了，请你用本章的一个知识来说明这样做的道理：． 14．（2分）一个多边形的一个顶点出发有5条对角线，这是一个边形． 15．（2分）如图，∠AOC和∠BOD都是直角，如果∠DOC=36°，则∠AOB是度． 16．（2分）48.13°=度分秒． 17．（2分）某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：排数 1 2 3 4座位数 50 53 56 59按这种方式排下去，第n排有个座位． 18．（2分）如果x＜0，y＞0且x2=4，y2=9，则x+y=．  三、解答题（前两小题题4分，后两小题5分，共18分）19．（18分）计算下列各题（1）（﹣7）+（+15）﹣（﹣25）（2）（﹣36）×（﹣+）（用运算律）（3）﹣24﹣×[5﹣（﹣3）2]（4）x2y﹣3xy2+2yx2﹣y2x．  四、综合应用题（共36分）20．（6分）图中是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，请画出这个几何体的主视图和左视图． 21．（6分）先化简，再求值：，其中． 22．（6分）把一个圆分割成三个扇形，它们圆心角的度数比为1：2：3，求最大的扇形的圆心角的度数． 23．（6分）如图，点A、O、E在同一直线上，∠AOB=40°，∠EOD=28°46′，OD平分∠COE，求∠COB的度数． 24．（6分）已知：如图，线段AB=16cm，E为AB的中点，C为AB上一点，D为AB延长线上的点，且CD=4cm，B为CD的中点．求线段EC和ED的长． 25．（6分）数a，b在数轴上的位置如图所示，化简：|a+b|﹣|a﹣b|+|a|﹣|b|．   广东省佛山市狮城中学2022学年七年级上学期第二次月考数学试卷参考答案与试题解析 一、选择题：（每题3分，共30分）1．（3分）﹣的倒数是（） A． ﹣2 B．  C． 2 D． ﹣ 考点： 倒数． 分析： 根据乘积为1的两个数互为倒数，可得一个数的倒数．解答： 解：﹣的倒数是﹣2，故选：A．点评： 本题考查了倒数，分子分母交换位置是求一个数的倒数的关键． 2．（3分）下列语句中，正确的是（） A． 直线比射线长 B． 射线比线段长 C． 无数条直线不可能相交于一点 D． 两条直线相交，只有一个交点 考点： 直线、射线、线段． 分析： 利用线段有两个端点，不能延伸；射线只有一个端点，可向射线延伸方向延伸；直线无端点，可两向延伸，来解答本题即可．解答： 解：∵线段有两个端点，不能延伸；射线只有一个端点，可向射线延伸方向延伸；直线无端点，可两向延伸，∴AB均不正确；C中由过一点可做无数条直线知，是不正确的；故只有D正确．故选D．点评： 本题考查的是线段、射线和直线的端点特征． 3．（3分）下列方程中是一元一次方程的是（） A． =7 B． y2﹣y=1 C． 2x﹣3y=1 D． ﹣3+x=1﹣x 考点： 一元一次方程的定义． 分析： 只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程．它的一般形式是ax+b=0（a，b是常数且a≠0）．解答： 解：A、不是整式方程，不是一元一次方程；B、未知项的最高次数为2，不是一元一次方程；C、含有两个未知数，不是一元一次方程；D、符合一元一次方程的定义．故选D．点评： 本题主要考查了一元一次方程的一般形式，只含有一个未知数，且未知数的指数是1，一次项系数不是0，这是这类题目考查的重点． 4．（3分）下列各题运算正确的是（） A． 3x+3y=6xy B． x+x=x2 C． ﹣9y2+16y2=7 D． 9a2b﹣9a2b=0 考点： 合并同类项． 分析： 根据同类项的定义及合并同类项法则解答．解答： 解：A、3x+3y不是同类项，不能合并，故A错误；B、x+x=2x≠x2，故B错误；C、﹣9y2+16y2=7y2≠7，故C错误；D、9a2b﹣9a2b=0，故D正确．故选：D．点评： 本题考查的知识点为：同类项的定义：所含字母相同，相同字母的指数相同；合并同类项的方法：字母和字母的指数不变，只把系数相加减；不是同类项的一定不能合并． 5．（3分）若|a|=2，则a=（） A． 2 B． ﹣2 C． 2或﹣2 D． 以上答案都不对 考点： 绝对值． 专题： 计算题．分析： 根据绝对值的意义可知：在数轴上到原点的距离是2的点有两个数，为2或﹣2．解答： 解：∵|a|=2，∴a=±2．故选C．点评： 注意：互为相反数的两个数的绝对值相等．运用数形结合的思想很容易解决此类问题． 6．（3分）下列方程中，以x=2为解的方程是（） A． x+2=0 B． 2x﹣1=0 C． 2x+4=6+3x D． 2x﹣4=6﹣3x 考点： 方程的解． 分析： 方程的解就是能够使方程两边左右相等的未知数的值，即利用方程的解代替方程中的未知数，所得到的式子左右两边相等．解答： 解：A、把x=2代入方程，左边=2+2=4≠右边，故选项错误；B、把x=2代入方程，左边=4﹣1=3≠右边，故选项错误；C、把x=2代入方程，左边=4+4=8，右边=6+6=12，则左边≠右边，故选项错误；D、把x=2代入方程，左边=4﹣4=0，右边6﹣6=0，则左边=右边，故是方程的解．故选D．点评： 本题主要考查了方程解的定义，方程的解就是能够使方程两边左右相等的未知数的值，理解定义是关键． 7．（3分）下列变形错误的是（） A． 由x+7=5，得x+7﹣7=5﹣7 B． 由3x﹣2=2x+1，得x=3 C． 由4﹣3x=4x﹣3，得4+3=4x+3x D． 由﹣2x=3，得x=﹣． 考点： 等式的性质． 分析： 根据等式的性质进行变形，再判断即可．解答： 解：A、x+7=5，则x+7﹣7=5﹣7，正确，不符合题意；B、3x﹣2=2x+1，3x﹣2x=1+2，x=3，正确，不符合题意；C、4﹣3x=4x﹣3，4+3=4x﹣3x，正确，不符合题意；D、﹣2x=3，x=﹣，错误，符合题意；故选D．点评： 本题考查了等式的性质的应用，主要考查学生的理解能力和判断能力．等式的性质是：①等式的两边都加上（或都减去）同一个数或同一个整式，所对的仍是等式，②等式的两边都乘以（或都除以）同一个不等于0的数，所对的仍是等式． 8．（3分）甲、乙、丙、丁四个学生判断时钟的分针与时针互相垂直时，他们每个人都说了两个时间，说对的是（） A． 甲说3点时和3点30分 B． 乙说6点15分和6点45分 C． 丙说9时整和12时15分 D． 丁说3时整和9时整 考点： 钟面角． 分析： 根据时针与分针相距的份数乘以每份的度数，可得答案．解答： 解：A、3点30分不到90°，故A错误；B、6点15分比90°多，故B错误；C、12时15分不到90°，故C错误；D、3时整和9时整钟面角都是90°，故D正确；故选：D．点评： 本题考查了钟面角，利用了时针与分针相距的份数乘以每份的度数． 9．（3分）如图，四条表示方向的射线中，表示北偏东60°的是（） A．  B C．   D．  考点： 方向角． 分析： 北偏东60°即由北向东偏60°，理解坐标上上北下南的表示方法．解答： 解：A中为南偏东60°，B中为北偏东60°，C中为北偏西30°，D中为北偏东30°，所以只有B符合题意，故选B．点评： 掌握方向角的表示方法． 10．（3分）同一平面内互不重合的三条直线的交点的个数是（） A． 可能是0个，1个，2个 B． 可能是0个，2个，3个 C． 可能是0个，1个，2个或3个 D． 可能是1个可3个 考点： 直线、射线、线段． 分析： 在同一平面内，两条直线的位置关系有两种，平行和相交，三条直线互相平行无交点，两条直线平行，第三条直线与它相交，有2个交点，三条直线两两相交，最多有3个交点，最少有1个交点．解答： 解：由题意画出图形，如图所示：故选C．点评： 本题考查了直线的交点个数问题． 二、填空题：（每题2分，共16分，）11．（2分）代数式的系数是． 考点： 单项式． 分析： 单项式的系数是指单项式中的数字因数，包括符号及分母的数字．解答： 解：代数式的数字因数是﹣，故单项式的系数是．点评： 本题考查了单项式的系数的概念．注意不要忘了符号和分母的数字． 12．（2分）若代数式3a5bm与﹣2a5b2是同类项，那么m=2． 考点： 同类项． 分析： 根据同类项：所含字母相同，并且相同字母的指数也相同，可得m的值．解答： 解：∵3a5bm与﹣2a5b2是同类项，∴m=2．故答案为：2．点评： 本题考查了同类项的知识，解答本题的关键是掌握同类项的定义． 13．（2分）七（1）班的同学用二个图钉就把刚获得的校田径运动会团体总分第一名的奖状挂在墙上了，请你用本章的一个知识来说明这样做的道理：过两点有且只有一条直线． 考点： 直线的性质：两点确定一条直线． 分析： 要把奖状挂在墙上，需要把奖状挂直，这就需要有一条直线来确保能够实现，过两点有且只有一条直线，可以满足要求．解答： 解：由题意知道奖状要挂在墙上必须挂直，需要确定一条直线来实现目的，即需要有两个图钉．利用的道理是：过两点有且只有一条直线．点评： 本题考查了直线的基本性质，实现了理论与实际的结合，题型不错． 14．（2分）一个多边形的一个顶点出发有5条对角线，这是一个八边形． 考点： 多边形的对角线． 分析： 根据n边形从一个顶点引出的对角线与边的关系：n﹣3，列方程求解．解答： 解：设多边形有n条边，则n﹣3=5，解得n=8．故多边形的边数为8，即它是八边形．故答案为八．点评： 本题考查了多边形的对角线，经过n边形的一个顶点所有的对角线有（n﹣3）条，经过n边形的一个顶点的所有对角线把n边形分成（n﹣2）个三角形． 15．（2分）如图，∠AOC和∠BOD都是直角，如果∠DOC=36°，则∠AOB是144度． 考点： 角的计算；余角和补角． 专题： 计算题．分析： 由余角的性质，结合角的计算求出结果．解答： 解：∵∠AOC和∠BOD都是直角，∠DOC=36°，∴∠AOD=54°．∴∠AOB=∠BOD+∠AOD=90°+54°=144°．点评： 此题主要考查了学生余角的性质，利用余角性质即可求出该角． 16．（2分）48.13°=48度7分48秒． 考点： 度分秒的换算． 分析： 根据度分秒的换算，大的单位化小的单位乘以进率，不满一度的化成分，不满一分的化成秒，可得答案．解答： 解：48.13°=48°7′48″，故答案为：48°7′48″．点评： 本题考查了度分秒的换算，把不满一度的化成分，不满一分的化成秒，都乘以进率60． 17．（2分）某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：排数 1 2 3 4座位数 50 53 56 59按这种方式排下去，第n排有（47+3n）个座位． 考点： 规律型：数字的变化类． 分析： 通过分析数据可知，观众席的座位每增加1排，就增加3个座位，再通过计算推断得出第n排的座位数．解答： 解：根据表格中数据所显示的规律可知：第1排有47+3×1=50个座位，第2排有47+3×2=53个座位，第3排有47+3×3=56个座位，第4排有47+3×4=59个座位，…则第n排有（47+3n）个座位．故答案为（47+3n）．点评： 主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解． 18．（2分）如果x＜0，y＞0且x2=4，y2=9，则x+y=1． 考点： 平方根；有理数的加法；有理数的乘方． 专题： 计算题．分析： x2=4即x是4的平方根，因而根据x＜0，y＞0且x2=4，y2=9，就可确定x，y的值，进而求解．解答： 解：∵x2=4，y2=9，∴x=±2，y=±3，又∵x＜0，y＞0，∴x=﹣2，y=3，∴x+y=﹣2+3=1．故答案为：1．点评： 本题主要考查了平方根的意义，根据条件正确确定x，y的值是解题关键． 三、解答题（前两小题题4分，后两小题5分，共18分）19．（18分）计算下列各题（1）（﹣7）+（+15）﹣（﹣25）（2）（﹣36）×（﹣+）（用运算律）（3）﹣24﹣×[5﹣（﹣3）2]（4）x2y﹣3xy2+2yx2﹣y2x． 考点： 有理数的混合运算；合并同类项． 专题： 计算题．分析： （1）原式利用减法法则变形，计算即可得到结果；（2）原式利用乘法分配律计算即可得到结果；（3）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可得到结果；（4）原式合并即可得到结果．解答： 解：（1）原式=﹣7+15+25=﹣7+40=33；（2）原式=﹣9+20﹣21=﹣10；（3）原式=﹣16+2=﹣14；（4）原式=3x2y﹣4y2x．点评： 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键． 四、综合应用题（共36分）20．（6分）图中是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，请画出这个几何体的主视图和左视图． 考点： 作图-三视图． 专题： 作图题．分析： 由已知条件可知，主视图有3列，每列小正方数形数目分别为2，3，4，左视图有2列，每列小正方形数目分别为4，3．据此可画出图形．解答： 解：点评： 本题考查几何体的三视图画法．由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视数的列数相同，且每列小正方形数目为俯视图中该列小正方形数字中的最大数字．左视图的列数与俯视图的行数相同，且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字． 21．（6分）先化简，再求值：，其中． 考点： 整式的加减—化简求值． 分析： 利用去括号法则先化简再求值．解答： 解：原式=3x﹣8x+2﹣+2x=﹣3x+，把x=﹣代入上式得：原式=﹣1．点评： 此题主要考查学生利用去括号法则先化简再求值的能力，学生做这类题时要认真细心． 22．（6分）把一个圆分割成三个扇形，它们圆心角的度数比为1：2：3，求最大的扇形的圆心角的度数． 考点： 角的概念． 分析： 首先根据题意，求出最大的扇形的圆心角占圆周角的=；然后根据分数乘法的意义，用360°乘以，求出最大的扇形的圆心角的度数是多少即可．解答： 解：360°×=360°×=180°．即最大的扇形的圆心角的度数是180°．点评： 此题主要考查了角的概念的应用，要熟练掌握，解答此题的关键是要明确：圆周角等于360°，并能判断出最大的扇形的圆心角的度数占圆周角的几分之几． 23．（6分）如图，点A、O、E在同一直线上，∠AOB=40°，∠EOD=28°46′，OD平分∠COE，求∠COB的度数． 考点： 角的计算． 专题： 计算题．分析： 根据角平分线的定义∠COD=∠EOD，所以∠COB的度数等于180°﹣∠AOB﹣∠EOD﹣∠COD，然后代入数据计算即可．解答： 解：∵∠EOD=28°46′，OD平分∠COE，∴∠COD=∠EOD=28°46′，∵∠AOB=40°，∴∠COB=180°﹣∠AOB﹣∠EOD﹣∠COD，=180°﹣40°﹣28°46′﹣28°46′，=82°28′．故答案为：82°28′．点评： 本题主要考查角的度数的运算，读懂图形分清角的和差关系比较重要，还要注意角是60进制，这也是同学们容易出错的地方． 24．（6分）已知：如图，线段AB=16cm，E为AB的中点，C为AB上一点，D为AB延长线上的点，且CD=4cm，B为CD的中点．求线段EC和ED的长． 考点： 两点间的距离． 分析： 先根据线段AB=16cm，E为AB的中点得出BE的长，再根据CD=4cm，B为CD的中点得出BC=BD=2，进而可得出结论．解答： 解：∵线段AB=16cm，E为AB的中点，∴BE=AB=8cm．∵CD=4cm，B为CD的中点，∴BC=BD=2cm，∴EC=EB﹣BC=8﹣2=6cm；ED=EB+BD=8+2=10cm．点评： 本题考查的是两点间的距离，熟知各线段之间的和、差及倍数关系是解答此题的关键． 25．（6分）数a，b在数轴上的位置如图所示，化简：|a+b|﹣|a﹣b|+|a|﹣|b|． 考点： 整式的加减；数轴；绝对值． 分析： 根据a、b在数轴上的位置可得，a＜0＜b，然后进行绝对值的化简，去括号，合并同类项求解．解答： 解：由图可得，a＜0＜b，则|a+b|﹣|a﹣b|+|a|﹣|b|=﹣a﹣b+a﹣b﹣a﹣b=﹣a﹣3b．点评： 本题考查了整式的加减，解答本题的关键是掌握绝对值的化简、合并同类项法则．