宁波市2022年初中学业水平考试明州卷数学试题(word版含答案)

展开

这是一份宁波市2022年初中学业水平考试明州卷数学试题(word版含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

宁波市2022年初中学业水平考试明州卷数学试题

试题卷
一、选择题(每小题 4 分,共 40 分. 在每小题给出旳四个选项中, 只有一项姩合题目要求)

1. 在这四个数中, 最小的数是( )
A. 2 B. 0 C. D.

2. 下列计算正确的是( )
A.
B.
C.
D.

3. “天问一号”在经历了7个月的“奔火”之旅和3个月的“环火”探测，完成了长达5亿千米的行程，登录器“祝融”号火星车于2021年5月15日7时18分从火星发来“短信”, 标志着我国首次火星登陠任务圆满成功, 请将5亿这个数用科学记数法依示为( )
A. B. C. D.

4. 如图III-1, 一个由圆柱和长方体组成的几何体水平放置, 它的俯视图是( )

5. 我市某一周内每天的最高气温如下表所示：

最高气温(C)	25	26	27	28
天数	1	1	2	3

则这组数据的中位数和众数分别是(    )
A. 和28     B. 27和28     C. 和3      D. 2和3
6. 若分式有意义, 则的取值范围是(    )
A.      B.      C.      D.
7. 两个直角三角板如图III-3摆放, 其中. 若且过点, 点为中点, 已知, 则的长为(    )
A. 15      B.        C.        D.

8.《九章算术》卷八方程第十题原文为: “今有甲、乙二人持钱不知其数. 甲得乙半而钱五十，乙得甲太半而亦钱五十。问：甲、乙持钱各几何？” 题目大意是：甲、乙两人各带了若干钱，如果甲得到乙所有钱得一般，那么甲共有钱50；如果乙得到甲所有钱的,那么乙也共有钱50 ,问：甲、乙两人各带了多少钱? 设甲、乙两人持钱的数量分别为 , 则可列方程组为(    )
A.                    B.
C.                    D.

9.一次函数与反比例函数在同一坐标系中的图象可能是( )

10. 两个全等的矩形和矩形如图III-5放置, 且恰好过点. 过点作平行交于. 知道下列哪个式子的值, 即可求出图中阴影部分的面积(    )
A.      B.      C.      D.

                              试题卷 II
二、填空题 (每小题5分, 共30分)

11. 的绝对值是________.

12. 分解因式________.

13. 一个不透明的袋中装有21个只有颜色不同的球,其中5个红球, 7个白球, 9个黄球. 从中任意摸出1个球是红球的概率为________.

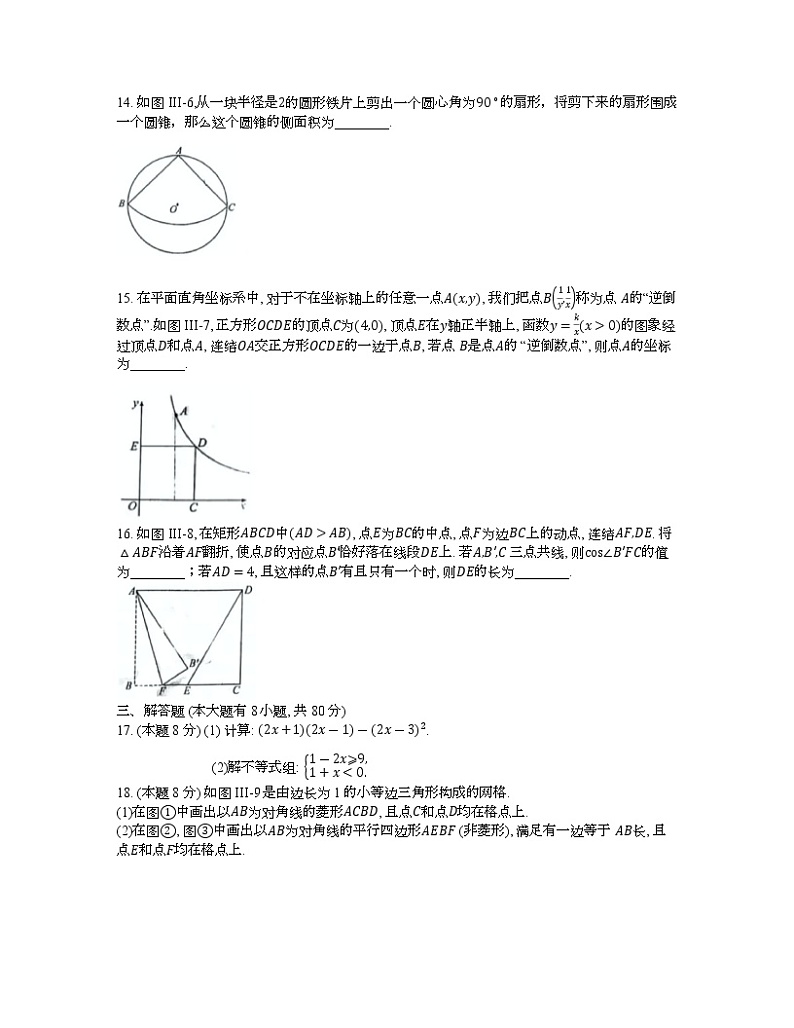
14. 如图III-6,从一块半径是圆心角为的扇形，将剪下来的扇形围成一个圆锥，那么这个圆锥的侧面积为________.

15. 在平面直角坐标系中, 对于不在坐标轴上的任意一点, 我们把点称为点的“逆倒数点”.如图III-7, 正方形的顶点为, 顶点在轴正半轴上, 函数的图象经过顶点和点, 连结交正方形的一边于点, 若点是点的 “逆倒数点”, 则点的坐标为________.

16. 如图III-8, 在矩形中, 点为的中点, 点为边上的动点, 连结. 将沿着翻折, 使点的对应点恰好落在线段上. 若三点共线, 则的值为________；若, 且这样的点有且只有一个时, 则的长为________.

三、解答题 (本大题有8小题, 共80分)
17. (本题 8 分) (1) 计算: .

(2)解不等式组:
18. (本题 8 分) 如图III-9是由边长为1的小等边三角形构成的网格.
(1)在图①中画出以为对角线的菱形, 且点和点均在格点上.
(2)在图②, 图③中画出以为对角线的平行四边形 (非菱形), 满足有一边等于长, 且点和点均在格点上.

19. (本题 8 分) 已知二次函数的部分图象如图III-10所示,
(1)求该二次函数图象的对称轴,并利用图象直接写出一元二次方程的解.

向上平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式。

20. (本题10分)在镇、村两委及帮扶人大力扶持下,贫困户周大叔与某公司签定了农产品销售合同,并于今年在自家荒坡上种植了四种不同品种的果树苗共300棵,其中品种果树苗的成活率为, 几个品种果树苗种植情况及其成活情况分别绘制在图III-11①和图②两个尚不完整的统计图中.
(1) 种植品种果树苗有多少棵;
(2)请你将图②的统计団补充完整;
(3)通过计算说明, 哪个品种的果树苗成活率最高.

21. (本题10分)为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制. 中小学楼梯宽度的范围是 (包括), 高度的范围是 (包括). 如图III-12是某中学的楼梯扶手的截面示意图，测量结果如下：分别垂直平分踏步EF,GH,各踏步互相平行, 结果精确到, 参考数据: )

22. (本题10分)周末, 自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练,甲、乙分别以不同的速度匀速骑行, 乙比甲早出发5分钟.乙骑行25分钟后, 甲以原速的继续骑行, 经过一段时间, 甲先到达地,乙一直保持原速前往地. 在此过程中,甲、乙两人相距的路程 (单位: 米)与乙骑行的时间 (单位: 分钟)之间的关系如图 III-13所示.
(1) 求甲、乙两人出发时的速度分别为多少米/分?
(2)甲、乙两人相遇时，甲出发了几分钟?
(3)乙比甲晩几分钟到达地?