2021中考数学真题知识点分类汇编-圆解答题1（含答案）

这是一份2021中考数学真题知识点分类汇编-圆解答题1（含答案），共50页。

2021中考数学真题知识点分类汇编-圆解答题1（含答案）

一．圆心角、弧、弦的关系（共1小题）
1．（2021•兴安盟）如图，AB是⊙O的直径，＝＝2，过点B作⊙O的切线BM交AD的延长线于点E．
（1）求证：AC＝CD；
（2）连接OE，若DE＝2，求OE的长．

二．圆周角定理（共7小题）
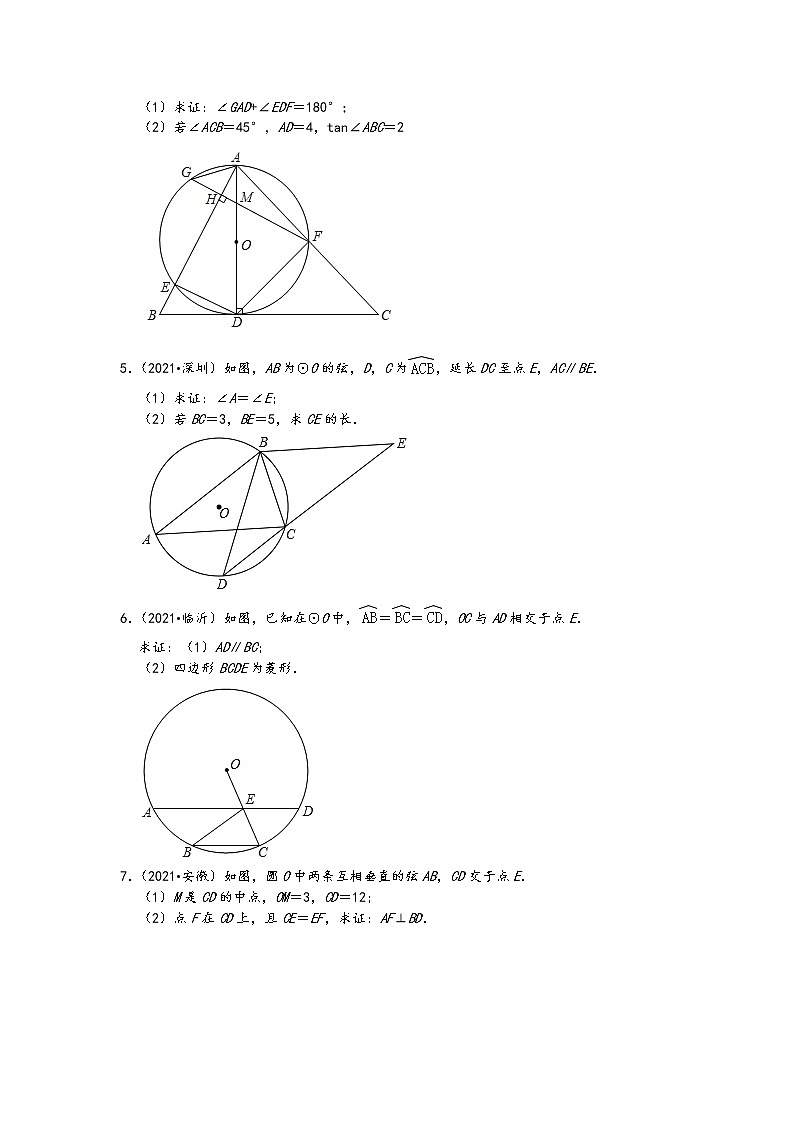
2．（2021•宁夏）如图，在△ABC中，点D是边BC上一点，点M是弦AC上一点，过点M作ME⊥BC，交BA的延长线于点F，且FA＝FM．
（1）求证：直线BF与半圆O相切；
（2）若已知AB＝3，求BD•BC的值．

3．（2021•徐州）如图，AB为⊙O的直径，点 C、D在⊙O上，AE＝EC，OE＝ED．连接BC、CD．求证：
（1）△AOE≌△CDE；
（2）四边形OBCD是菱形．

4．（2021•包头）如图，在锐角三角形ABC中，AD是BC边上的高，交AC于点F，过点F作FG⊥AB，交于点G，交AD于点M，DE，DF．
（1）求证：∠GAD+∠EDF＝180°；
（2）若∠ACB＝45°，AD＝4，tan∠ABC＝2

5．（2021•深圳）如图，AB为⊙O的弦，D，C为，延长DC至点E，AC∥BE．
（1）求证：∠A＝∠E；
（2）若BC＝3，BE＝5，求CE的长．

6．（2021•临沂）如图，已知在⊙O中，＝＝，OC与AD相交于点E．
求证：（1）AD∥BC；
（2）四边形BCDE为菱形．

7．（2021•安徽）如图，圆O中两条互相垂直的弦AB，CD交于点E．
（1）M是CD的中点，OM＝3，CD＝12；
（2）点F在CD上，且CE＝EF，求证：AF⊥BD．

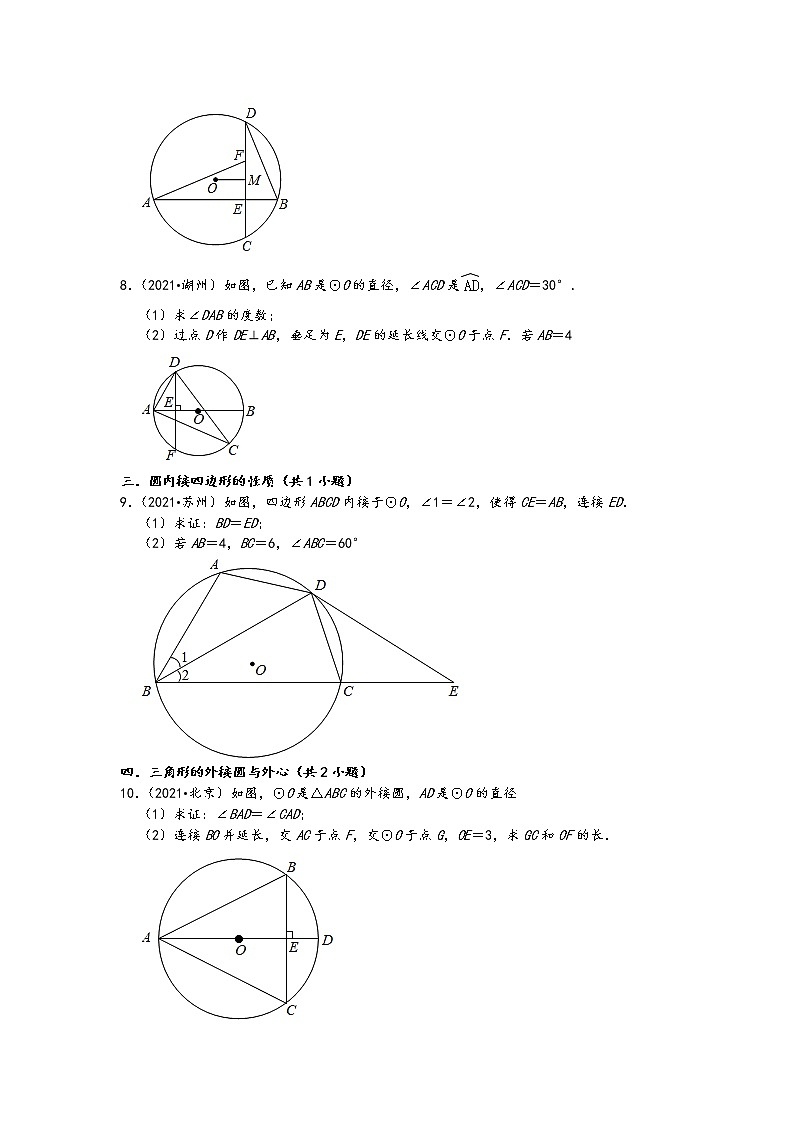
8．（2021•湖州）如图，已知AB是⊙O的直径，∠ACD是，∠ACD＝30°．
（1）求∠DAB的度数；
（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB＝4

三．圆内接四边形的性质（共1小题）
9．（2021•苏州）如图，四边形ABCD内接于⊙O，∠1＝∠2，使得CE＝AB，连接ED．
（1）求证：BD＝ED；
（2）若AB＝4，BC＝6，∠ABC＝60°

四．三角形的外接圆与外心（共2小题）
10．（2021•北京）如图，⊙O是△ABC的外接圆，AD是⊙O的直径
（1）求证：∠BAD＝∠CAD；
（2）连接BO并延长，交AC于点F，交⊙O于点G，OE＝3，求GC和OF的长．

11．（2021•荆门）如图，在△ABC中，∠BAC＝90°，过A，C，E三点的⊙O交AB边于另一点F的中点，AD是⊙O的一条直径
（1）求证：四边形CDMF为平行四边形；
（2）当CD＝AB时，求sin∠ACF的值．

五．直线与圆的位置关系（共4小题）
12．（2021•镇江）如图1，正方形ABCD的边长为4，点P在边BC上，B，P三点．
（1）若BP＝3，判断边CD所在直线与⊙O的位置关系，并说明理由；
（2）如图2，E是CD的中点，⊙O交射线AE于点Q，求tan∠EAP的值．

13．（2021•淮安）如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O的直径．

14．（2021•赤峰）如图，在菱形ABCD中，对角线AC、BD相交于点M，C，交对角线BD于点E，且＝，连接OE交BC于点F．
（1）试判断AB与⊙O的位置关系，并说明理由；
（2）若BD＝，tan∠CBD＝，求⊙O的半径．

15．（2021•宿迁）如图，在Rt△AOB中，∠AOB＝90°，OA为半径的圆交AB于点C，点D在边OB上
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）已知tan∠ODC＝，AB＝40，求⊙O的半径．

六．切线的性质（共14小题）
16．如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，垂足为点F．
（1）求证：AB＝BC；
（2）若⊙O的直径AB为9，sinA＝．
①求线段BF的长；
②求线段BE的长．

17．（2021•陕西）如图，DP是⊙O的切线，D为切点，连接BO并延长，与⊙O交于点C，连接AC并延长，与DP交于点F
（1）求证：AF∥OD；
（2）若OD＝5，AB＝8，求线段EF的长．

18．（2021•黔西南州）如图，AB为⊙O的直径，直线l与⊙O相切于点C，垂足为D，AD交⊙O于点E
（1）求证：∠CAD＝∠CAB；
（2）若EC＝4，sin∠CAD＝，求⊙O的半径．

19．（2021•济南）已知：如图，AB是⊙O的直径，C，D是⊙O上两点，DE⊥CE，连接CD
（1）求证：∠DAB＝2∠ABC；
（2）若tan∠ADC＝，BC＝4，求⊙O的半径．

20．（2021•南通）如图，AB为⊙O的直径，C为⊙O上一点，垂足为D，∠CAD＝35°
（1）求∠B的度数；
（2）若AB＝2，求的长．

21．（2021•大连）如图1，△ABC内接于⊙O，直线MN与⊙O相切于点D，BC∥MN．
（1）求证：∠BAC＝∠DOC；
（2）如图2，若AC是⊙O的直径，E是OD的中点，求AE的长．

22．（2021•湘西州）如图，AB为⊙O的直径，C为⊙O上一点，垂足为D．
（1）求证：AC平分∠DAB；
（2）若AD＝8，tan∠CAB＝，求：边AC及AB的长．

23．（2021•贺州）如图，在Rt△ABC中，∠C＝90°，以AD为直径的⊙O与BC相切于点E，连接AE
（1）求证：AE平分∠BAC；
（2）若∠B＝30°，求的值．

24．（2021•齐齐哈尔）如图，AB为⊙O的直径，C为⊙O上的一点，垂足为E，AE与⊙O相交于点F
（1）求证：AC平分∠EAB；
（2）若AE＝12，tan∠CAB＝，求OB的长．

25．（2021•鄂州）如图，在Rt△ABC中，∠ABC＝90°，以O为圆心，OB长为半径的⊙O与AC边相切于点D
（1）求证：AB＝AD；
（2）连接DE，若tan∠EDC＝，DE＝2

26．（2021•河南）在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”．
小明受此启发设计了一个“双连杆机构”，设计图如图1，两个固定长度的“连杆”AP，当点P在⨀O上转动时，带动点A，ON上滑动，OM⊥ON．当AP与⨀O相切时，如图2．
请仅就图2的情形解答下列问题．
（1）求证：∠PAO＝2∠PBO；
（2）若⨀O的半径为5，AP＝，求BP的长．

27．（2021•陕西）如图，AB是⊙O的直径，点E、F在⊙O上，且，连接OE、AF，过点B作⊙O的切线
（1）求证：∠COB＝∠A；
（2）若AB＝6，CB＝4，求线段FD的长．

28．（2021•天津）已知△ABC内接于⊙O，AB＝AC，∠BAC＝42°
（Ⅰ）如图①，若BD为⊙O的直径，连接CD；
（Ⅱ）如图②，若CD∥BA，连接AD，与OC的延长线交于点E，求∠E的大小．

29．（2021•泸州）如图，△ABC是⊙O的内接三角形，过点C作⊙O的切线交BA的延长线于点F，连接EC．
（1）求证：∠ACF＝∠B；
（2）若AB＝BC，AD⊥BC于点D，FC＝4，求AD•AE的值．

七．三角形的内切圆与内心（共1小题）
30．（2021•毕节市）如图，⊙O是△ABC的外接圆，点E是△ABC的内心，交⊙O于点D，连接BD
（1）求证：DB＝DE；
（2）若AE＝3，DF＝4，求DB的长．

八．正多边形和圆（共1小题）
31．（2021•河北）如图，⊙O的半径为6，将该圆周12等分后得到表盘模型n（n为1～12的整数），过点A7作⊙O的切线交A1A11延长线于点P．
（1）通过计算比较直径和劣弧长度哪个更长；
（2）连接A7A11，则A7A11和PA1有什么特殊位置关系？请简要说明理由；
（3）求切线长PA7的值．

九．扇形面积的计算（共2小题）
32．（2021•贵阳）如图，在⊙O中，AC为⊙O的直径，点E是的中点，交AB于点M，交⊙O于点N，CN．
（1）EM与BE的数量关系是 　 　；
（2）求证：＝；
（3）若AM＝，MB＝1，求阴影部分图形的面积．

33．（2021•扬州）如图，四边形ABCD中，AD∥BC，CB＝CD，连接BD，BA长为半径作⊙B，交BD于点E．
（1）试判断CD与⊙B的位置关系，并说明理由；
（2）若AB＝2，∠BCD＝60°，求图中阴影部分的面积．

一十．圆锥的计算（共1小题）
34．（2021•邵阳）某种冰激凌的外包装可以视为圆锥，它的底面圆直径ED与母线AD长之比为1：2．制作这种外包装需要用如图所示的等腰三角形材料，其中AB＝AC，AE，AF恰好重合．
（1）求这种加工材料的顶角∠BAC的大小．
（2）若圆锥底面圆的直径ED为5cm，求加工材料剩余部分（图中阴影部分）的面积．（结果保留π）


参考答案与试题解析
一．圆心角、弧、弦的关系（共1小题）
1．（2021•兴安盟）如图，AB是⊙O的直径，＝＝2，过点B作⊙O的切线BM交AD的延长线于点E．
（1）求证：AC＝CD；
（2）连接OE，若DE＝2，求OE的长．

【解析】证明：（1）∵＝＝2，
∴AD＝CD，B是CD的中点，
∵AB是直径，
∴AD＝AC，
∴AC＝CD；
（2）如图，连接BD，

∵AD＝DC＝AC，
∴∠ADC＝∠DAC＝60°，
∵CD⊥AB，
∴∠DAB＝∠DAC＝30°，
∵BM切⊙O于点B，AB是直径，
∴BM⊥AB，
∵CD⊥AB，
∴BM∥CD，
∴∠AEB＝∠ADC＝60°，
∵AB是直径，
∴∠ADB＝90°，
在Rt△BDE中，
∵∠DBE＝90°﹣∠DEB＝30°，
∴BE＝2DE＝4，
∴BD＝＝＝7，
在Rt△BDA中，
∵∠DAB＝30°，
∴AB＝2BD＝3，
∴OB＝AB＝2，
在Rt△OBE中，OE＝＝．
二．圆周角定理（共7小题）
2．（2021•宁夏）如图，在△ABC中，点D是边BC上一点，点M是弦AC上一点，过点M作ME⊥BC，交BA的延长线于点F，且FA＝FM．
（1）求证：直线BF与半圆O相切；
（2）若已知AB＝3，求BD•BC的值．

【解析】（1）证明：如图，连接AO．

∵FE⊥BC，
∴∠CEM＝90°，
∴∠C+∠CME＝90°，
∵FA＝FM，
∴∠FAM＝∠FMA＝∠CME，
∵OA＝OC，
∴∠C＝∠OAC，
∴∠FAM+∠OAC＝90°，
∴∠OAF＝90°，
∴OA⊥AB，
∵OA是半径，
∴BF是⊙O的切线．

（2）解：连接AD．
∵CD是直径，
∴∠DAC＝90°，
∴∠C+∠ADC＝90°，
∵∠BAO＝90°，
∴∠BAD+∠OAD＝90°，
∵OA＝OD，
∴∠OAD＝∠ODA，
∴∠BAD+∠ADC＝90°，
∴∠BAD＝∠C，
∵∠B＝∠B，
∴△BAD∽△BCA，
∴＝，
∴BD•BC＝BA2＝9．
3．（2021•徐州）如图，AB为⊙O的直径，点 C、D在⊙O上，AE＝EC，OE＝ED．连接BC、CD．求证：
（1）△AOE≌△CDE；
（2）四边形OBCD是菱形．

【解析】证明：（1）在△AOE和△CDE中，
，
∴△AOE≌△CDE（SAS）；
（2）∵△AOE≌△CDE，
∴OA＝CD，∠AOE＝∠D，
∴OB∥CD，
∵OA＝OB，
∴OB＝CD，
∴四边形OBCD为平行四边形，
∵OB＝OD，
∴四边形OBCD是菱形．

4．（2021•包头）如图，在锐角三角形ABC中，AD是BC边上的高，交AC于点F，过点F作FG⊥AB，交于点G，交AD于点M，DE，DF．
（1）求证：∠GAD+∠EDF＝180°；
（2）若∠ACB＝45°，AD＝4，tan∠ABC＝2

【解析】（1）证明：由题可知∠AGF＝∠ADF（同弧所对的圆周角相等），
∵GF⊥AB，AD为圆的直径，
∴∠AGF+∠GAE＝90°，∠ADF+∠FAD＝90°，
∴∠GAE＝∠FAD，
∴∠GAE+∠DAE＝∠FAD+∠DAE，即∠GAD＝∠EAF，
∵四边形AEDF是圆的内接四边形，
∴∠EAF+∠EDF＝180°，
∴∠GAD+∠EDF＝180°．
（2）解：如图，

连接OF，
∵AD是圆的直径，且AD是△ABC的高，
∴∠AED＝∠ADB＝∠AHM＝∠AFD＝90°，
∵∠HAM＝∠DAB，
∴△AHM∽△ADB，
∴＝，
∵tan∠ABC＝＝2，
∴＝2，
∵∠ACB＝45°，
∴∠DAC＝∠ADF＝∠AFO＝45°，
∴∠AOF＝90°，
∵在Rt△AHM与Rt△FOM中：∠AMH＝∠FMO（对顶角），
∴△AHM∽△FOM，
∴＝＝5，
∵AD＝4，
∴OF＝OA＝2，
∴＝7，AM＝OA﹣OM＝1，
设HM＝x，则AH＝2x，
在Rt△AHM中有：AH6+HM2＝AM2，
即（6x）2+x2＝3，解得x1＝，x2＝﹣（舍去），
∴AH＝，
∵OF＝OA＝2，
∴AF＝2，
在Rt△AHF中，有：AH2+HF2＝AF6，
即（）2+HF2＝（5）2，
解得HF＝，或HF＝﹣，
故HF的长为．
5．（2021•深圳）如图，AB为⊙O的弦，D，C为，延长DC至点E，AC∥BE．
（1）求证：∠A＝∠E；
（2）若BC＝3，BE＝5，求CE的长．

【解析】（1）证明：
∵AC∥BE，
∴∠E＝∠ACD，
∵D，C为，
∴＝＝，
∴∠ACD＝∠A，
∴∠E＝∠A，
（2）解：由（1）知＝＝，
∴∠D＝∠CBD＝∠A＝∠E，
∴BE＝BD＝5，BC＝CD＝3，
∴＝，即，
解得DE＝，
∴CE＝DE﹣CD＝﹣3＝．
6．（2021•临沂）如图，已知在⊙O中，＝＝，OC与AD相交于点E．
求证：（1）AD∥BC；
（2）四边形BCDE为菱形．

【解析】证明：（1）连接BD，
∵，
∴∠ADB＝∠CBD，
∴AD∥BC；

（2）连接CD，BD，
∵AD∥BC，
∴∠EDF＝∠CBF，
∵，
∴BC＝CD，BF＝DF，
又∠DFE＝∠BFC，
∴△DEF≌△BCF（ASA），
∴DE＝BC，
∴四边形BCDE是平行四边形，又BC＝CD，
∴四边形BCDE是菱形．
7．（2021•安徽）如图，圆O中两条互相垂直的弦AB，CD交于点E．
（1）M是CD的中点，OM＝3，CD＝12；
（2）点F在CD上，且CE＝EF，求证：AF⊥BD．

【解析】解：（1）连接OD，如图：

∵M是CD的中点，CD＝12，
∴DM＝CD＝4，∠OMD＝90°，
Rt△OMD中，OD＝，
∴OD＝＝3；
（2）连接AC，延长AF交BD于G

∵AB⊥CD，CE＝EF，
∴AB是CF的垂直平分线，
∴AF＝AC，即△ACF是等腰三角形，
∵CE＝EF，
∴∠FAE＝∠CAE，
∵＝，
∴∠CAE＝∠CDB，
∴∠FAE＝∠CDB，
Rt△BDE中，∠CDB+∠B＝90°，
∴∠FAE+∠B＝90°，
∴∠AGB＝90°，
∴AG⊥BD，即AF⊥BD．
8．（2021•湖州）如图，已知AB是⊙O的直径，∠ACD是，∠ACD＝30°．
（1）求∠DAB的度数；
（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB＝4

【解析】解：（1）如图，连接BD，

∵∠ACD＝30°，
∴∠B＝∠ACD＝30°，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∴∠DAB＝90°﹣∠B＝60°；
（2）∵∠ADB＝90°，∠B＝30°，
∴AD＝AB＝5，
∵∠DAB＝60°，DE⊥AB，
∴EF＝DE＝ADsin60°＝，
∴DF＝2DE＝4．
三．圆内接四边形的性质（共1小题）
9．（2021•苏州）如图，四边形ABCD内接于⊙O，∠1＝∠2，使得CE＝AB，连接ED．
（1）求证：BD＝ED；
（2）若AB＝4，BC＝6，∠ABC＝60°

【解析】（1）证明：∵四边形ABCD内接于⊙O，
∴∠A＝∠DCE，
∵∠1＝∠2，
∴＝，
∴AD＝DC，
在△ABD和△DCE中，
，
∴△ABD≌△CED（SAS），
∴BD＝ED；
（2）解：过点D作DM⊥BE于M，
∵AB＝6，BC＝6，
∴BE＝BC+EC＝10，
∵BD＝ED，DM⊥BE，
∴BM＝ME＝BE＝5，
∴CM＝BC﹣BM＝1，
∵∠ABC＝60°，∠5＝∠2，
∴∠2＝30°，
∴DM＝BM•tan∠8＝5×＝，
∴tan∠DCB＝＝．

四．三角形的外接圆与外心（共2小题）
10．（2021•北京）如图，⊙O是△ABC的外接圆，AD是⊙O的直径
（1）求证：∠BAD＝∠CAD；
（2）连接BO并延长，交AC于点F，交⊙O于点G，OE＝3，求GC和OF的长．

【解析】（1）证明：∵AD是⊙O的直径，AD⊥BC，
∴＝，
∴∠BAD＝∠CAD；
（2）解：在Rt△BOE中，OB＝5，
∴BE＝＝4，
∵AD是⊙O的直径，AD⊥BC，
∴BC＝2BE＝6，
∵BG是⊙O的直径，
∴∠BCG＝90°，
∴GC＝＝2，
∵AD⊥BC，∠BCG＝90°，
∴AE∥GC，
∴△AFO∽△CFG，
∴＝，即＝，
解得：OF＝．

11．（2021•荆门）如图，在△ABC中，∠BAC＝90°，过A，C，E三点的⊙O交AB边于另一点F的中点，AD是⊙O的一条直径
（1）求证：四边形CDMF为平行四边形；
（2）当CD＝AB时，求sin∠ACF的值．

【解析】（1）证明：连接DF、EF，
∵∠BAC＝90°，
∴FC是⊙O的直径，
∵F是的中点，
∴＝，
∴∠ADF＝∠EDF，
∵OF＝OD，
∴∠ADF＝∠OFD，
∴∠OFD＝∠EDF，
∴FC∥DM，
∵OA＝OD，OF＝OC，
∴四边形AFDC为矩形，
∴AF∥CD，
∴四边形CDMF为平行四边形；
（2）解：∵四边形AFDC为矩形，四边形CDMF为平行四边形，
∴CD＝AF＝FM＝EF，
∵CD＝AB，
∴CD＝（2CD+BM），
∴CD＝8BM，
∵BM∥CD，
∴△BEM∽△CED，
∴＝＝，
∴EC＝5BE，
设BM＝a，则CD＝2a，EF＝2a，
在Rt△BEF中，BE＝＝a，
∴EC＝5a，
在Rt△CEF中，FC＝a，
在Rt△FAC中，sin∠ACF＝＝＝．

五．直线与圆的位置关系（共4小题）
12．（2021•镇江）如图1，正方形ABCD的边长为4，点P在边BC上，B，P三点．
（1）若BP＝3，判断边CD所在直线与⊙O的位置关系，并说明理由；
（2）如图2，E是CD的中点，⊙O交射线AE于点Q，求tan∠EAP的值．

【解析】解：（1）如图1﹣1中，连接AP，交CD于E．

∵四边形ABCD是正方形，
∴AB＝AD＝2，∠ABP＝90°，
∴AP是直径，
∴AP＝＝＝5，
∵OH⊥AB，
∴AH＝BH，
∵OA＝OP，AH＝HB，
∴OH＝PB＝，
∵∠D＝∠DAH＝∠AHE＝90°，
∴四边形AHED是矩形，
∴OE⊥CE，EH＝AD＝2，
∴OE＝EH﹣OH＝4﹣＝，
∴OE＝OP，
∴直线CD与⊙O相切．

（2）如图3中，延长AE交BC的延长线于T．

∵∠D＝∠ECT＝90°，DE＝EC，
∴△ADE≌△TCE（ASA），
∴AD＝CT＝4，
∴BT＝BC+CT＝4+6＝8，
∵∠ABT＝90°，
∴AT＝＝＝4，
∵AP是直径，
∴∠AQP＝90°，
∵PA平分∠EAB，PQ⊥AQ，
∴PB＝PQ，
设PB＝PQ＝x，
∵S△ABT＝S△ABP+S△APT，
∴×5×8＝×x+，
∴x＝2﹣3，
∴tan∠EAP＝tan∠PAB＝＝．
备注：本题也可以用面积法，连接PQ，设BP＝x，

在Rt△PEQ中，
PE2＝x2+（3﹣4）8，
在Rt△PEC中，
PE2＝（4﹣x）6+22，
则x5+（2﹣5）2＝（4﹣x）8+22，
解得x＝PB＝2﹣2，
∴tan∠EAP＝tan∠PAB＝＝．
13．（2021•淮安）如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O的直径．

【解析】（1）证明：连接DO，如图，

∵直径所对圆周角，
∴∠ADC＝90°，
∴∠BDC＝90°，E为BC的中点，
∴DE＝CE＝BE，
∴∠EDC＝∠ECD，
又∵OD＝OC，
∴∠ODC＝∠OCD，
而∠OCD+∠DCE＝∠ACB＝90°，
∴∠EDC+∠ODC＝90°，即∠EDO＝90°，
∴DE⊥OD且OD为半径，
∴DE与⊙O相切；

（2）由（1）得，∠CDB＝90°，
∵CE＝EB，
∴DE＝BC，
∴BC＝2，
∴BD＝＝＝4，
∵∠BCA＝∠BDC＝90°，∠B＝∠B，
∴△BCA∽△BDC，
∴＝，
∴＝，
∴AC＝，
∴⊙O直径的长为．
14．（2021•赤峰）如图，在菱形ABCD中，对角线AC、BD相交于点M，C，交对角线BD于点E，且＝，连接OE交BC于点F．
（1）试判断AB与⊙O的位置关系，并说明理由；
（2）若BD＝，tan∠CBD＝，求⊙O的半径．

【解析】解：（1）AB是⊙O的切线，
理由如下：
连接OB，
∵OE＝OB，
∴∠OEB＝∠OBE，
∵四边形ABCD是菱形，AC，
∴∠ABD＝∠CBD，
∵＝，OE是⊙O的半径，
∴OE⊥BC，
∴∠BFE＝90°，
∴∠OEB+∠CBE＝90°，
∴∠ABD+∠OBE＝90°，
∴OB⊥AB，即AB是⊙O的切线；
（2）∵四边形ABCD是菱形，AC，BD＝，
∴BM＝BD＝，
∵tan∠CBD＝，
∴CM＝BM＝，
∴BC＝＝8，
∵＝，OE是⊙O的半径，
∴BF＝BC＝4，
∵tan∠CBD＝，OE⊥BC，
∴EF＝BF＝3，
设⊙O的半径为r，则OF的长为r﹣2，
在Rt△OFB中，
OF2+BF6＝OB2，即（r﹣2）8+42＝r5，
解得：r＝5，
∴⊙O的半径为5．

15．（2021•宿迁）如图，在Rt△AOB中，∠AOB＝90°，OA为半径的圆交AB于点C，点D在边OB上
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）已知tan∠ODC＝，AB＝40，求⊙O的半径．

【解析】解：（1）直线CD与⊙O相切，
理由如下：如图，连接OC，

∵OA＝OC，CD＝BD，
∴∠A＝∠ACO，∠B＝∠DCB，
∵∠AOB＝90°，
∴∠A+∠B＝90°，
∴∠ACO+∠DCB＝90°，
∴∠OCD＝90°，
∴OC⊥CD，
又∵OC为半径，
∴CD是⊙O的切线，
∴直线CD与⊙O相切；
（2）∵tan∠ODC＝＝，
∴设CD＝7x＝DB，OC＝24x＝OA，
∵∠OCD＝90°，
∴OD＝＝＝25x，
∴OB＝32x，
∵∠AOB＝90°，
∴AB2＝AO2+OB2，
∴1600＝576x2+1024x2，
∴x＝6，
∴OA＝OC＝24，
∴⊙O的半径为24．
六．切线的性质（共14小题）
16．如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，垂足为点F．
（1）求证：AB＝BC；
（2）若⊙O的直径AB为9，sinA＝．
①求线段BF的长；
②求线段BE的长．

【解析】解：（1）证明：连接OD，如图1，

∵DE是⊙O的切线，
∴OD⊥DE．
∵BC⊥DE，
∴OD∥BC．
∴∠ODA＝∠C．
∵OA＝OD，
∴∠ODA＝∠A．
∴∠A＝∠C．
∴AB＝BC．
（2）①连接BD，则∠ADB＝90°，

在Rt△ABD中，
∵sinA＝，AB＝9，
∴BD＝3．
∵OB＝OD，
∴∠ODB＝∠OBD．
∵∠OBD+∠A＝∠FDB+∠ODB＝90°，
∴∠A＝∠FDB．
∴sin∠A＝sin∠FDB．
在Rt△BDF中，
∵sin∠BDF＝＝，
∴BF＝1．
②由（1）知：OD∥BF，
∴△EBF∽△EOD．
∴．
即：．
解得：BE＝．
17．（2021•陕西）如图，DP是⊙O的切线，D为切点，连接BO并延长，与⊙O交于点C，连接AC并延长，与DP交于点F
（1）求证：AF∥OD；
（2）若OD＝5，AB＝8，求线段EF的长．

【解析】（1）证明：延长DO交AB于点H，
∵DP是⊙O的切线，
∴OD⊥DP，
∵AB∥DP，
∴HD⊥AB，
∵BC为⊙O的直径，
∴∠BAC＝90°，
∴AF∥OD；
（2）∵OH⊥AB，AB＝8，
∴BH＝AH＝4，
∴OH＝＝＝4，
∵BH∥ED，
∴△BOH∽△EOD，
∴＝，即＝，
解得：ED＝，
∵∠BAC＝90°，DH⊥AB，
∴四边形AFDH为矩形，
∴DF＝AH＝4，
∴EF＝ED﹣DF＝﹣4＝．

18．（2021•黔西南州）如图，AB为⊙O的直径，直线l与⊙O相切于点C，垂足为D，AD交⊙O于点E
（1）求证：∠CAD＝∠CAB；
（2）若EC＝4，sin∠CAD＝，求⊙O的半径．

【解析】（1）证明：连接OC，
∵CD为⊙O的切线，
∴OC⊥CD，
∵AD⊥CD，
∴OC∥AD，
∴∠CAD＝∠ACO．
又∵OC＝OA，
∴∠ACO＝∠OAC，
∴∠CAD＝∠OAC，
即∠CAD＝∠BAC；
（2）解：连接BC，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠B+∠CAB＝90°，
∴∠CAD+∠B＝90°，
∵∠CED＝∠B，∠CED+∠ECD＝90°，
∴∠DCE＝∠CAD，
∵sin∠CAD＝sin∠DCE＝＝，
∴DE＝，
∴CD＝＝，
∴AC＝8，
∵∠BAC＝∠CAD，
∴sin∠CAD＝sin∠BAC＝＝，
∴设AB＝3x，BC＝x，
∴AC＝2x＝8，
∴x＝4，
∴AB＝3x＝12，
∴⊙O的半径为8．
方法二：∵∠CAD＝∠BAC，
∴EC＝CB＝4，
连接BC，
∵AB是直径，
∴∠ACB＝90°，
∴sin∠CAB＝，
∴AB＝12，

∴半径为6

19．（2021•济南）已知：如图，AB是⊙O的直径，C，D是⊙O上两点，DE⊥CE，连接CD
（1）求证：∠DAB＝2∠ABC；
（2）若tan∠ADC＝，BC＝4，求⊙O的半径．

【解析】（1）证明：连接OC，
∵EC是⊙O的切线，
∴OC⊥CE，
∵DE⊥CE，
∴OC∥DE，
∴∠DAB＝∠AOC，
由圆周角定理得：∠AOC＝2∠ABC，
∴∠DAB＝2∠ABC；
（2）解：连接AC，
∵AB是⊙O的直径，
∴∠ACB＝90°，
由圆周角定理得：∠ABC＝∠ADC，
∴tan∠ABC＝tan∠ADC＝，即＝，
∵BC＝4，
∴AC＝2，
由勾股定理得：AB＝＝＝7，
∴⊙O的半径为．

20．（2021•南通）如图，AB为⊙O的直径，C为⊙O上一点，垂足为D，∠CAD＝35°
（1）求∠B的度数；
（2）若AB＝2，求的长．

【解析】解：（1）连接OC，如图，

∵CD是⊙O的切线，
∴OC⊥CD，
∵AE⊥CD，
∴OC∥AE，
∴∠CAD＝∠OCA，
∵OA＝OC，
∴∠OCA＝∠OAC，
∴∠CAD＝∠OAC＝35°，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠OAC+∠B＝90°，
∴∠B＝90°﹣∠OAC＝90°﹣35°＝55°；

（2）连接OE，
∵⊙O的直径AB＝2，
∴OA＝1，
∵＝，
∴∠COE＝5∠CAE＝2×35°＝70°，
∴的长为：＝．

21．（2021•大连）如图1，△ABC内接于⊙O，直线MN与⊙O相切于点D，BC∥MN．
（1）求证：∠BAC＝∠DOC；
（2）如图2，若AC是⊙O的直径，E是OD的中点，求AE的长．

【解析】（1）证明：连接OB，如图1，

∵直线MN与⊙O相切于点D，
∴OD⊥MN，
∵BC∥MN，
∴OD⊥BC，
∴＝，
∴∠BOD＝∠COD，
∵∠BAC＝∠BOC，
∴∠BAC＝∠COD；
（2）∵E是OD的中点，
∴OE＝DE＝2，
在Rt△OCE中，CE＝＝，
∵OE⊥BC，
∴BE＝CE＝4，
∵AC是⊙O的直径，
∴∠ABC＝90°，
∴AB＝＝＝3，
在Rt△ABE中，AE＝＝．
22．（2021•湘西州）如图，AB为⊙O的直径，C为⊙O上一点，垂足为D．
（1）求证：AC平分∠DAB；
（2）若AD＝8，tan∠CAB＝，求：边AC及AB的长．

【解析】（1）证明：连接OC，如图，
∵CD为⊙O的切线，
∴OC⊥CD，
∵AD⊥CD，
∴OC∥AD，
∴∠DAC＝∠OCA，
∵OA＝OC，
∴∠OAC＝∠OCA，
∴∠DAC＝∠OAC，
∴AC平分∠DAB；
（2）解：连接BC，如图，
∵∠DAC＝∠OAC，
∴tan∠DAC＝tan∠CAB＝，
在Rt△DAC中，∵tan∠DAC＝＝，
∴CD＝×8＝6，
∴AC＝＝＝10，
∵AB为直径，
∴∠ACB＝90°，
∴tan∠CAB＝＝，
∴BC＝×10＝，
∴AB＝＝．

23．（2021•贺州）如图，在Rt△ABC中，∠C＝90°，以AD为直径的⊙O与BC相切于点E，连接AE
（1）求证：AE平分∠BAC；
（2）若∠B＝30°，求的值．

【解析】（1）证明：连接OE，
∵BC是⊙O的切线，
∴OE⊥BC，即∠OEB＝90°，
∵∠C＝90°，
∴OE∥AC，
∴∠OEA＝∠EAC，
∵OE＝OA，
∴∠OEA＝∠OAE，
∴∠OAE＝∠EAC，即AE平分∠BAC；
（2）解：∵AD为⊙O的直径，
∴∠AED＝90°，
∵∠OAE＝∠EAC，∠C＝90°，
∴△DAE∽△EAC，
∴＝，
∵∠C＝90°，∠B＝30°，
∴∠BAC＝90°﹣30°＝60°，
∴∠DAE＝∠BAC＝30°，
∵cos∠DAE＝，cos30°＝，
∴＝＝．

24．（2021•齐齐哈尔）如图，AB为⊙O的直径，C为⊙O上的一点，垂足为E，AE与⊙O相交于点F
（1）求证：AC平分∠EAB；
（2）若AE＝12，tan∠CAB＝，求OB的长．

【解析】（1）证明：连接OC，
∵CD为⊙O的切线，
∴OC⊥DE，
∵AE⊥DE，
∴OC∥AE，
∴∠EAC＝∠OCA，
∵OA＝OC，
∴∠OAC＝∠OCA，
∴∠EAC＝∠OAC，即AC平分∠EAB；
（2）解：连接BC，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∵tan∠CAB＝，∠EAC＝∠OAC，
∴tan∠EAC＝，即＝，
∴＝，
解得：EC＝5，
在Rt△AEC中，AC＝＝，
∵tan∠CAB＝＝，
∴BC＝8，
在Rt△ABC中，AB＝＝，
∴OB＝5．

25．（2021•鄂州）如图，在Rt△ABC中，∠ABC＝90°，以O为圆心，OB长为半径的⊙O与AC边相切于点D
（1）求证：AB＝AD；
（2）连接DE，若tan∠EDC＝，DE＝2

【解析】（1）证明：∵∠ABC＝90°，
∴AB⊥OB，
∵AB经过⊙O半径的外端点B，
∴AB切⊙O于点B，
又⊙O与AC边相切于点D，
∴AB＝AD．
（2）解：如图，

连接BD，
∵BE为⊙O的直径，
∴∠BDE＝90°，
∴∠CDE+∠ADB＝90°，
又∵AB＝AD，
∴∠ADB＝∠ABD，
∴∠CDE+∠ABD＝90°，
∵∠ABC＝90°，
∴∠ABD+∠EBD＝90°，
∴∠EBD＝∠EDC，
又∵，
∴，
即，
∵DE＝2，
∴BD＝4，，
又∵∠C＝∠C，∠EBD＝∠EDC，
∴△CDE∽△CBD，
∴，
设CE＝x，则DC＝2x，
∴，
∴x7＝0（舍去），，
即线段EC的长为．
26．（2021•河南）在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”．
小明受此启发设计了一个“双连杆机构”，设计图如图1，两个固定长度的“连杆”AP，当点P在⨀O上转动时，带动点A，ON上滑动，OM⊥ON．当AP与⨀O相切时，如图2．
请仅就图2的情形解答下列问题．
（1）求证：∠PAO＝2∠PBO；
（2）若⨀O的半径为5，AP＝，求BP的长．

【解析】（1）证明：如图①，

连接OP，延长BO与圆交于点C，
∵AP与⨀O相切于点P，
∴∠APO＝90°，
∴∠PAO+∠AOP＝90°，
∵MO⊥CN，
∴∠AOP+∠POC＝90°，
∴∠PAO＝∠POC，
∵OP＝OB，
∴∠OPB＝∠PBO，
∴∠POC＝∠OPB+∠PBO＝2∠PBO，
∴∠PAO＝2∠PBO；
（2）解：如图②所示，

连接OP，延长BO与圆交于点C，过点P作PD⊥OC于点D，
则有：AO＝＝，
由（1）可知∠POC＝∠PAO，
∴Rt△POD∽Rt△OAP，
∴，即，解得PD＝3，
∴CD＝OC﹣OD＝1，
在Rt△PDC中，PC＝＝，
∵CB为圆的直径，
∴∠BPC＝90°，
∴BP＝＝＝3，
故BP长为3．
27．（2021•陕西）如图，AB是⊙O的直径，点E、F在⊙O上，且，连接OE、AF，过点B作⊙O的切线
（1）求证：∠COB＝∠A；
（2）若AB＝6，CB＝4，求线段FD的长．

【解析】（1）证明：取的中点M、OF，
∵＝2，
∴＝＝，
∴∠COB＝∠BOF，
∵∠A＝∠BOF，
∴∠COB＝∠A；
（2）解：连接BF，如图，
∵CD为⊙O的切线，
∴AB⊥CD，
∴∠OBC＝∠ABD＝90°，
∵∠COB＝∠A，
∴△OBC∽△ABD，
∴＝，即＝，解得BD＝6，
在Rt△ABD中，AD＝＝，
∵AB是⊙O的直径，
∴∠AFB＝90°，
∵∠BDF＝∠ADB，
∴Rt△DBF∽Rt△DAB，
∴＝，即＝，解得DF＝．

28．（2021•天津）已知△ABC内接于⊙O，AB＝AC，∠BAC＝42°
（Ⅰ）如图①，若BD为⊙O的直径，连接CD；
（Ⅱ）如图②，若CD∥BA，连接AD，与OC的延长线交于点E，求∠E的大小．

【解析】解：（Ⅰ）如图①，∵AB＝AC，
∴∠ABC＝∠ACB＝（180°﹣∠BAC）＝，
∵BD为直径，
∴∠BCD＝90°，
∵∠D＝∠BAC＝42°，
∴∠DBC＝90°﹣∠D＝90°﹣42°＝48°；
∴∠ACD＝∠ABD＝∠ABC﹣∠DBC＝69°﹣48°＝21°；
（Ⅱ）如图②，连接OD，
∵CD∥AB，
∴∠ACD＝∠BAC＝42°，
∵四边形ABCD为⊙O的内接四边形，
∴∠B+∠ADC＝180°，
∴∠ADC＝180°﹣∠B＝180°﹣69°＝111°，
∴∠CAD＝180°﹣∠ACD﹣∠ADC＝180°﹣42°﹣111°＝27°，
∴∠COD＝2∠CAD＝54°，
∵DE为切线，
∴OD⊥DE，
∴∠ODE＝90°，
∴∠E＝90°﹣∠DOE＝90°﹣54°＝36°．

29．（2021•泸州）如图，△ABC是⊙O的内接三角形，过点C作⊙O的切线交BA的延长线于点F，连接EC．
（1）求证：∠ACF＝∠B；
（2）若AB＝BC，AD⊥BC于点D，FC＝4，求AD•AE的值．

【解析】（1）证明：如图1，连接OC，

∵CF是⊙O的切线，
∴∠OCF＝90°，
∴∠OCA+∠ACF＝90°，
∵OE＝OC，
∴∠E＝∠OCE，
∵AE是⊙O的直径，
∴∠ACE＝90°，
∴∠OCA+∠OCE＝90°，
∴∠ACF＝∠OCE＝∠E，
∵∠B＝∠E，
∴∠ACF＝∠B；
（2）解：∵∠ACF＝∠B，∠F＝∠F，
∴△ACF∽△CBF，
∴＝，
∵AF＝2，CF＝8，
∴，
∴BF＝8，
∴AB＝BC＝8﹣3＝6，AC＝3，
∵AD⊥BC，
∴∠ADB＝∠ACE＝90°，
∵∠B＝∠E，
∴△ABD∽△AEC，
∴＝，即AE•AD＝AB×AC＝7×3＝18．
七．三角形的内切圆与内心（共1小题）
30．（2021•毕节市）如图，⊙O是△ABC的外接圆，点E是△ABC的内心，交⊙O于点D，连接BD
（1）求证：DB＝DE；
（2）若AE＝3，DF＝4，求DB的长．

【解析】（1）证明：∵点E是△ABC的内心，
∴AE平分∠BAC，BE平分∠ABC，
∴∠BAD＝∠CAD，∠ABE＝∠CBE，
又∵∠CAD与∠CBD所对弧为，
∴∠CAD＝∠CBD＝∠BAD．
∴∠BED＝∠ABE+∠BAD，∠DBE＝∠CBE+∠CBD，
即∠BED＝∠DBE，
故DB＝DE．
（2）解：∵∠D＝∠D，∠DBF＝∠CAD＝∠BAD，
∴△ABD∽△BFD，
∴①，
∵DF＝4，AE＝3，
由（1）可得DB＝DE＝5+x，
则①式化为，
解得：x1＝6，x2＝﹣6（不符题意，舍去），
则DB＝5+x＝4+2＝8．
八．正多边形和圆（共1小题）
31．（2021•河北）如图，⊙O的半径为6，将该圆周12等分后得到表盘模型n（n为1～12的整数），过点A7作⊙O的切线交A1A11延长线于点P．
（1）通过计算比较直径和劣弧长度哪个更长；
（2）连接A7A11，则A7A11和PA1有什么特殊位置关系？请简要说明理由；
（3）求切线长PA7的值．

【解析】解：（1）由题意，∠A7OA11＝120°，
∴的长＝，
∴比直径长．

（2）结论：PA1⊥A7A11．
理由：连接A1A7，A3A11，OA11．
∵A1A7是⊙O的直径，
∴∠A2A11A1＝90°，
∴PA1⊥A5A11．

（3）∵PA7是⊙O的切线，
∴PA7⊥A5A7，
∴∠PA7A4＝90°，
∵∠PA1A7＝60°，A5A7＝12，
∴PA7＝A4A7•tan60°＝12．

九．扇形面积的计算（共2小题）
32．（2021•贵阳）如图，在⊙O中，AC为⊙O的直径，点E是的中点，交AB于点M，交⊙O于点N，CN．
（1）EM与BE的数量关系是 　BE＝EM　；
（2）求证：＝；
（3）若AM＝，MB＝1，求阴影部分图形的面积．

【解析】解：（1）∵AC为⊙O的直径，点E是，
∴∠ABE＝45°，
∵AB⊥EN，
∴△BME是等腰直角三角形，
∴BE＝EM，
故答案为BE＝EM；

（2）连接EO，
∵AC是⊙O的直径，E是，
∴∠AOE＝90°，
∴∠ABE＝∠AOE＝45°，
∵EN⊥AB，垂足为点M，
∴∠EMB＝90°
∴∠ABE＝∠BEN＝45°，
∴＝，
∵点E是的中点，
∴＝，
∴＝，
∴﹣＝﹣，
∴＝；

（3）连接AE，OB，
∵EN⊥AB，垂足为点M，
∴∠AME＝∠EMB＝90°，
∵BM＝1，由（2）得∠ABE＝∠BEN＝45°，
∴EM＝BM＝2，
又∵BE＝EM，
∴BE＝，
∵在Rt△AEM中，EM＝4，
∴tan∠EAB＝＝，
∴∠EAB＝30°，
∵∠EAB＝∠EOB，
∴∠EOB＝60°，
又∵OE＝OB，
∴△EOB是等边三角形，
∴OE＝BE＝，
又∵＝，
∴BE＝CN，
∴△OEB≌△OCN（SSS），
∴CN＝BE＝
又∵S扇形OCN＝＝，S△OCN＝CN××＝，
∴S阴影＝S扇形OCN﹣S△OCN＝﹣．

33．（2021•扬州）如图，四边形ABCD中，AD∥BC，CB＝CD，连接BD，BA长为半径作⊙B，交BD于点E．
（1）试判断CD与⊙B的位置关系，并说明理由；
（2）若AB＝2，∠BCD＝60°，求图中阴影部分的面积．

【解析】解：（1）过点B作BF⊥CD，垂足为F，
∵AD∥BC，
∴∠ADB＝∠CBD，
∵CB＝CD，
∴∠CBD＝∠CDB，
∴∠ADB＝∠CDB．
在△ABD和△FBD中，
，
∴△ABD≌△FBD（AAS），
∴BF＝BA，则点F在圆B上，
∴CD与⊙B相切；


（2）∵∠BCD＝60°，CB＝CD，
∴△BCD是等边三角形，
∴∠CBD＝60°
∵BF⊥CD，
∴∠ABD＝∠DBF＝∠CBF＝30°，
∴∠ABF＝60°，
∵AB＝BF＝，
∴AD＝DF＝AB·tan30°＝3，
∴阴影部分的面积＝S△ABD﹣S扇形ABE
＝
＝．
一十．圆锥的计算（共1小题）
34．（2021•邵阳）某种冰激凌的外包装可以视为圆锥，它的底面圆直径ED与母线AD长之比为1：2．制作这种外包装需要用如图所示的等腰三角形材料，其中AB＝AC，AE，AF恰好重合．
（1）求这种加工材料的顶角∠BAC的大小．
（2）若圆锥底面圆的直径ED为5cm，求加工材料剩余部分（图中阴影部分）的面积．（结果保留π）

【解析】解：（1）设∠BAC＝n°．
由题意得π•DE＝，AD＝2DE，
∴n＝90，
∴∠BAC＝90°．

（2）∵AD＝2DE＝10（cm），
∴S阴＝•BC•AD﹣S扇形AEF＝×10×20﹣2．