2022年浙江省杭州市上城区九年级下学期学情调查考试（二模）数学试题(word版含答案)

2022年浙江省杭州市上城区九年级下学期学情调查考试（二模）数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．如果与互为相反数，那么等于（       ）

A． B．8 C． D．

2．下列计算正确的是（       ）

A． B．

C． D．

3．田径运动会上，有20名运动员参加了跳高比赛，其中19名运动员的成绩统计如下：

不论最后一位运动员的成绩如何，这组数据中不会发生改变的统计量是（       ）A．平均数              B．中位数              C．众数              D．方差

4．若，则下列各不等式正确的是（       ）

A． B． C． D．

5．已知半径为6的扇形，面积为12π，则扇形的弧长为(   )

A．4 B．4π C．2π D．2

6．数学课上，同学们讨论了如下习题：“一组同学一起去种树．如果每人种4棵，还剩下3棵树苗；如果每人种5棵，则缺少5棵树苗．”设这组同学有人，需种植树苗棵．则根据题意列出的方程（组）正确的是（       ）

A． B．

C． D．

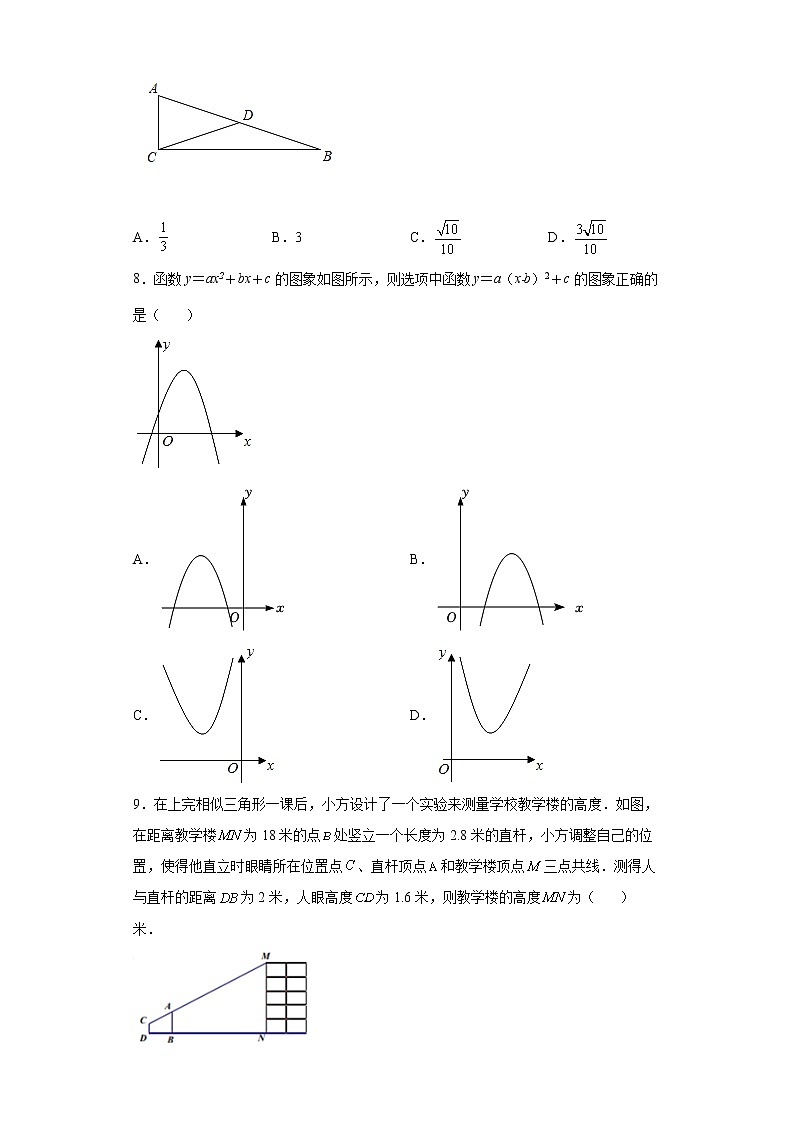
7．如图，在中，，D为的中点，，则（       ）

A． B．3 C． D．

8．函数y＝ax2＋bx＋c的图象如图所示，则选项中函数y＝a（x﹣b）2＋c的图象正确的是（       ）

A． B．

C． D．

9．在上完相似三角形一课后，小方设计了一个实验来测量学校教学楼的高度．如图，在距离教学楼为18米的点处竖立一个长度为2.8米的直杆，小方调整自己的位置，使得他直立时眼睛所在位置点、直杆顶点和教学楼顶点三点共线．测得人与直杆的距离为2米，人眼高度为1.6米，则教学楼的高度为（       ）米．

A．12 B．12.4 C．13.6 D．15.2

10．如图，四边形ABCD内接于⊙O，AB为⊙O的直径，延长BA与弦CD的延长线交于点P，已知PD=AB，下列结论：①若=+，则AB=CD；②若∠B=60°，则∠P=20°；③若∠P=30°，则=−1；④的值可能等于．其中正确的序号是（       ）

A．①②③ B．①②④ C．②③④ D．①③④

二、填空题

11．因式分解： _________.

12．如图所示，，则的度数为______．

13．一个两位数，它的十位数字是1，个位数字是抛掷一枚质地均匀的骰子（六个面分别标有数字1-6）朝上一面的数字．任意抛掷这枚骰子一次，得到的两位数是4的倍数概率等于______．

14．已知方程x2−3x+m=0有两个实数根，则m所取的值可以是______．（填一个即可）

15．已知点和点为平面直角坐标系内两点，且点的坐标为，将点向右平移3个单位至点，则线段上任意一点的坐标可表示为______．

16．如图，在中，，点在边上．连接，将沿直线翻折，点落在点处，交边于点．已知，，若为直角三角形，则的面积为______．

三、解答题

17．已知：，求代数式的值．

18．旅客在网购高铁车票时，系统是随机分配座位的．小王和小李打算购买从杭州到北京的高铁车票（如图所示，同一排的座位编号为A，B，C，D，F），假设系统已将两人分配到同一排后，在同一排分配各个座位的机会是均等的．

(1)求系统将王某安排到靠窗座位的概率；

(2)求系统分配给王某和李某相邻座位（过道两侧座位C，D不算相邻）的概率．

19．如图，点是上一点．

(1)请用直尺和圆规过点作出的一条切线；（不要求写出作法，不要求证明，但要保留作图痕迹）

(2)若（1）所作切线上取一点，满足，若半径为2，求的长．

20．验光师测得一组关于近视眼镜的度数（度）与镜片焦距（米）的对应数据如下表：

(1)请写出适当的函数表达式描述近视眼镜的度数与镜片焦距的关系；

(2)小张同学通过科学的视力矫正和良好的用眼习惯，有效抑制近视度数增长．一年来他的近视眼镜的度数从原来的150度变化到现在的175度，则他所佩戴眼镜的镜片焦距增加还是减少了？增加或减少多少？

21．如图1所示的晾衣架，支架的基本图形是菱形．如图2，晾衣架伸缩时，点在射线上滑动，菱形的形状也随之发生变化．已知每个菱形的边长均等于，且．

(1)求证：相邻两根晾衣架之间的水平距离（、）相等；

(2)当晾衣架沿着方向平移时，的度数逐渐减小．若从120°逐渐减小到60°时，求点在射线上移动的距离．

22．二次函数的自变量与函数值的对应值如下表：

(1)若，求此时函数解析式；

(2)当时，对应的函数值．

①和在该二次函数的图象上，试比较与大小；

②求的范围．

23．正方形边长为3，点是上一点，连接交于点．

(1)如图1，若，求的值；

(2)如图1，若，求证：点是的中点；

(3)如图2，点为上一点，且满足，设，，试探究与的函数关系．

参考答案：

1．B

2．B

3．C

4．D

5．B

6．D

7．B

8．B

9．C

10．A

11．

12．125°

13．

14．2

15．（x，1）（）

16．或

17．4

18．(1)

(2)

19．(1)见解析

(2)

20．(1)

(2)他所佩戴眼镜的镜片焦距减少了米．

21．(1)见解析

(2)

22．(1)

(2)①；②

23．(1)；

(2)见解析；

(3)（0≤x≤3）；