




2022年高考理科数学押题预测卷+答案解析01(全国乙卷)
展开2022年高考押题预测卷01(全国乙卷)
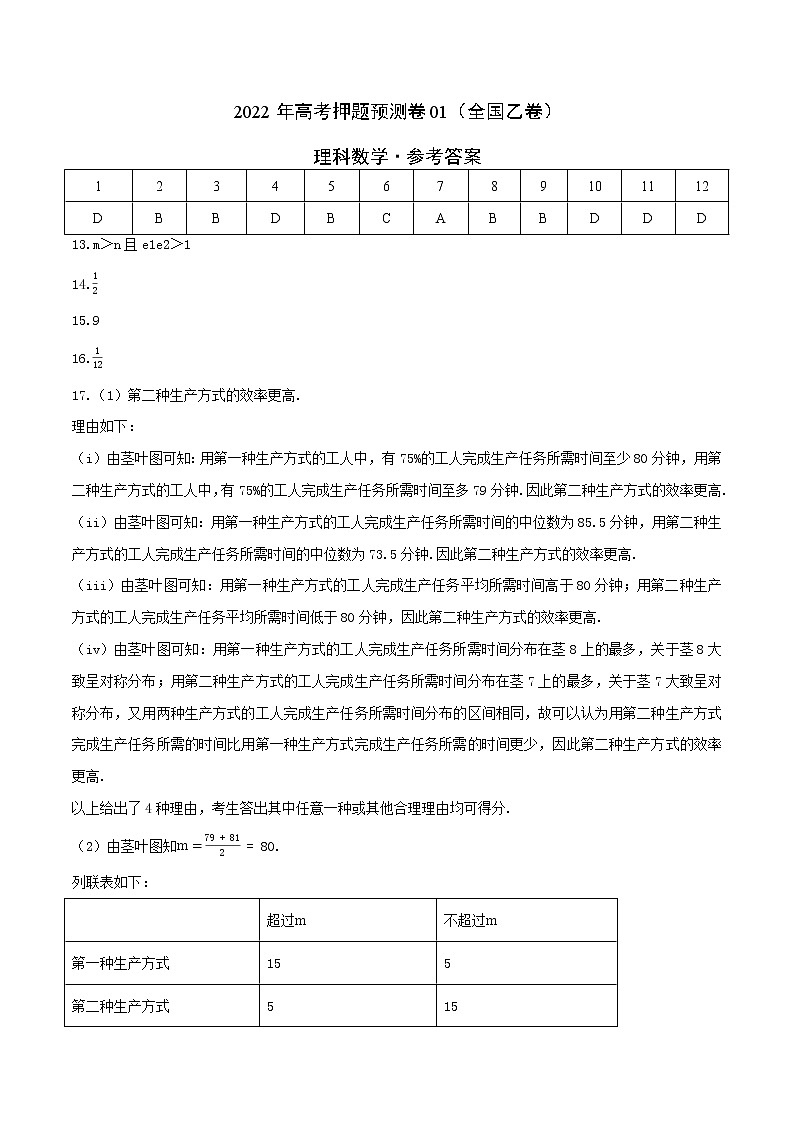
理科数学·参考答案
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
D | B | B | D | B | C | A | B | B | D | D | D |
13.m>n且e1e2>1
14.
15.9
16.
17.(1)第二种生产方式的效率更高.
理由如下:
(i)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.
(ii)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.
(iii)由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.
(iv)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.
以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分.
(2)由茎叶图知.
列联表如下:
| 超过 | 不超过 |
第一种生产方式 | 15 | 5 |
第二种生产方式 | 5 | 15 |
(3)由于,所以有99%的把握认为两种生产方式的效率有差异.
18.(1)证明 由已知得AM=AD=2.
取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.
又AD∥BC,故TN綉AM,四边形AMNT为平行四边形,于是MN∥AT.
因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.
(2)解 取BC的中点E,连接AE.由AB=AC得AE⊥BC,
从而AE⊥AD,AE===.
以A为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系A-xyz.
由题意知,P(0,0,4),M(0,2,0),C(,2,0),N,=(0,2,-4),=,=.
设n=(x,y,z)为平面PMN的法向量,则即
可取n=(0,2,1).于是cos〈n,〉==.
设AN与平面PMN所成的角为θ,则sin θ=,
∴直线AN与平面PMN所成的角的正弦值为.
19.解 (1)由题意有,即
解得或故或
(2)由d>1,知an=2n-1,bn=2n-1,故cn=,于是
Tn=1+++++…+,①
Tn=+++++…+.②
①-②可得
Tn=2+++…+-=3-,故Tn=6-.
20.解(1)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).
①设a=0,则f(x)=(x-2)ex,f(x)只有一个零点.
②设a>0,则当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,所以f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.
又f(1)=-e,f(2)=a,取b满足b<0且b<ln,则f(b)>(b-2)+a(b-1)2=a>0,故f(x)存在两个零点.
③设a<0,由f′(x)=0得x=1或x=ln(-2a).
若a≥-,则ln(-2a)≤1,故当x∈(1,+∞)时,f′(x)>0,因此f(x)在(1,+∞)上单调递增.
又当x≤1时,f(x)<0,所以f(x)不存在两个零点.
若a<-,则ln(-2a)>1,
故当x∈(1,ln(-2a))时,f′(x)<0;当x∈(ln(-2a),+∞)时,f′(x)>0,因此f(x)在(1,ln(-2a))上单调递减,在(ln(-2a),+∞)上单调递增.
又当x≤1时,f(x)<0,所以f(x)不存在两个零点.
综上,a的取值范围为(0,+∞).
(2)不妨设x1<x2.由(1)知,x1∈(-∞,1),x2∈(1,+∞),2-x2∈(-∞,1),f(x)在(-∞,1)上单调递减,所以x1+x2<2等价于f(x1)>f(2-x2),即f(2-x2)<0.
由于f(2-x2)=-x2e2-x2+a(x2-1)2,而f(x2)=(x2-2)ex2+a(x2-1)2=0,
所以f(2-x2)=-x2e2-x2-(x2-2)ex2.
设g(x)=-xe2-x-(x-2)ex,则g′(x)=(x-1)(e2-x-ex),所以当x>1时,g′(x)<0,而g(1)=0,
故当x>1时,g(x)<0,从而g(x2)=f(2-x2)<0,故x1+x2<2.
21.(Ⅰ)将点代入抛物线方程:可得:,
故抛物线方程为:,其准线方程为:.
(Ⅱ)很明显直线的斜率存在,焦点坐标为,
设直线方程为,与抛物线方程联立可得:.
故:.
设,则,
直线的方程为,与联立可得:,同理可得,
易知以AB为直径的圆的圆心坐标为:,圆的半径为:,
且:,,
则圆的方程为:,
令整理可得:,解得:,
即以AB为直径的圆经过y轴上的两个定点.
22.(1)的直角坐标方程为.
当时,与交于两点.
当时,记,则的方程为.与交于两点当且仅当,解得或,即或.
综上,的取值范围是.
(2)的参数方程为为参数, .
设,,对应的参数分别为,,,则,且,满足.
于是,.又点的坐标满足
所以点的轨迹的参数方程是 为参数, .
23.解 (1)当a=2时,f(x)=|2x-2|+2.解不等式|2x-2|+2≤6得-1≤x≤3.
因此f(x)≤6的解集为{x|-1≤x≤3}.
(2)当x∈R时,f(x)+g(x)=|2x-a|+a+|1-2x|≥|2x-a+1-2x|+a=|1-a|+a,
所以当x∈R时,f(x)+g(x)≥3等价于|1-a|+a≥3.①
当a≤1时,①等价于1-a+a≥3,无解.
当a>1时,①等价于a-1+a≥3,解得a≥2.
所以a的取值范围是[2,+∞).
2023年高考押题预测卷01(乙卷理科)(参考答案)数学: 这是一份2023年高考押题预测卷01(乙卷理科)(参考答案)数学,共7页。
2022年高考理科数学押题预测卷+答案解析01(全国甲卷): 这是一份2022年高考理科数学押题预测卷+答案解析01(全国甲卷),文件包含理科数学-2022年高考押题预测卷01全国甲卷全解全析docx、理科数学-2022年高考押题预测卷01全国甲卷参考答案docx、理科数学-2022年高考押题预测卷01全国甲卷考试版docx等3份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
2022年高考理科数学押题预测卷+答案解析02(全国乙卷): 这是一份2022年高考理科数学押题预测卷+答案解析02(全国乙卷),文件包含理科数学-2022年高考押题预测卷02全国乙卷全解全析docx、理科数学-2022年高考押题预测卷02全国乙卷参考答案docx、理科数学-2022年高考押题预测卷02全国乙卷考试版docx等3份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。












