数学必修第一册5.3 函数的单调性教案配套课件ppt

展开

这是一份数学必修第一册5.3 函数的单调性教案配套课件ppt，共19页。

1.函数单调性的概念一般地,设函数y=f(x)的定义域为A,区间I⊆A.如果对于区间I内的任意两个值x1,x2, 当x1f(x2)    , 那么称y=f(x)在区间I上是减函数,I称为y=f(x)的减区间(如图2).
1 | 函数的单调性
2.函数的单调区间如果函数y=f(x)在区间I上是增函数或减函数,那么称函数y=f(x)在区间I上具有单调性.增区间和减区间统称为单调区间.
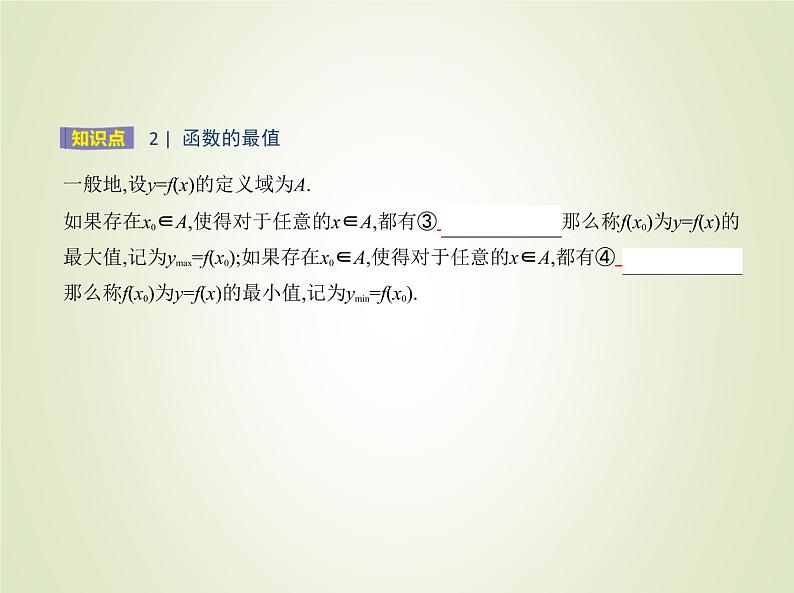
一般地,设y=f(x)的定义域为A.如果存在x0∈A,使得对于任意的x∈A,都有③    f(x)≤f(x0)    ,那么称f(x0)为y=f(x)的最大值,记为ymax=f(x0);如果存在x0∈A,使得对于任意的x∈A,都有④    f(x)≥f(x0)    , 那么称f(x0)为y=f(x)的最小值,记为ymin=f(x0).
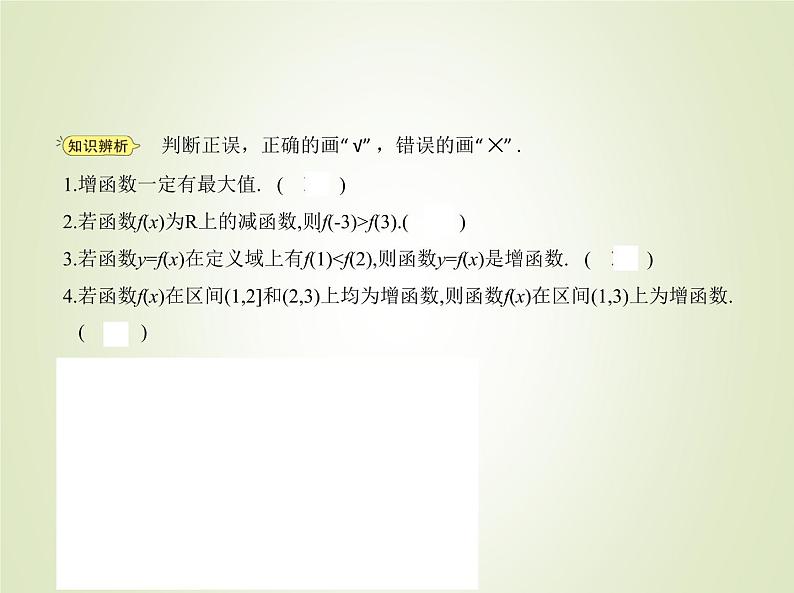
1.增函数一定有最大值. (    ✕　)2.若函数f(x)为R上的减函数,则f(-3)>f(3).(　√　)3.若函数y=f(x)在定义域上有f(1)判断正误，正确的画“ √” ，错误的画“ ✕” .
5.若函数f(x)在区间[a,b]上是增函数,则f(x)在区间[a,b]上的最小值是f(a),最大值是 f(b). (　√　)提示:由于函数f(x)在区间[a,b]上是增函数,所以f(a)≤f(x)≤f(b).故f(x)的最小值是f(a),最大值是f(b).
1 | 函数单调性的判定
判断函数单调性的常用方法1.定义法.根据增函数、减函数的定义,按照“取值→作差→变形→判断符号→下结论”进行判断.单调性判断的等价结论:当x∈D时, f(x)是增函数,∀x1,x2∈D且x1≠x2,(x1-x2)[f(x1)-f(x2)]>0⇔ >0.当x∈D时, f(x)是减函数,∀x1,x2∈D且x1≠x2,(x1-x2)[f(x1)-f(x2)]<0⇔ <0.2.图象法.根据函数图象的升降情况进行判断.
3.直接法.运用已知结论,直接得到函数的单调性,如一次函数、二次函数、反比例函数的单调性均可直接得出.4.利用常见结论.在公共定义域内,
(1)增函数+增函数是增函数;(2)减函数+减函数是减函数;(3)增函数-减函数是增函数;(4)减函数-增函数是减函数.
复合函数单调性的判定复合函数单调性的判断依据如下:(1)若u=g(x),y=f(u)在所讨论的区间上都是增函数或都是减函数,则y=f(g(x))为增函数;(2)若u=g(x),y=f(u)在所讨论的区间上一个是增函数,另一个是减函数,则y=f(g(x))为减函数.列表如下:
复合函数的单调性可简记为“同增异减”,即内外函数的单调性相同时单调递增,相异时单调递减.
设函数f(x)的定义域是(0,+∞),且对任意正实数x,y都有f(xy)=f(x)+f(y)恒成立,已知f(2)=1,且当x>1时, f(x)>0.(1)求f 的值;(2)判断y=f(x)在(0,+∞)上的单调性并证明.
思路点拨(1)抽象函数问题解决的关键是根据结论对x,y进行赋值,通过赋值解决;(2)利用定义判断函数的单调性.
解析    (1)∵对任意正实数x,y都有f(xy)=f(x)+f(y)恒成立,∴当x=y=1时,有f(1)=f(1)+f(1),∴f(1)=0.当x=2,y= 时,有f =f(2)+f ,即f(2)+f =0,又f(2)=1,∴f =-1.(2)y=f(x)在(0,+∞)上为增函数.证明如下:设x1,x2为区间(0,+∞)上的任意两个值,且x11,∴f >0,即f(x2)>f(x1),∴f(x)在(0,+∞)上为增函数.
2 | 函数单调性的应用
利用函数的单调性解不等式1.利用函数的单调性解不等式主要依据函数单调性的概念,将符号“f ”脱掉,列出关于未知量的不等式(组),然后求解,此时注意函数的定义域.2.解有关抽象函数的不等式问题的一般步骤:(1)将不等式化为f(x1)x2.
利用函数的单调性求参数的取值范围的方法1.利用单调性的定义:在单调区间内任取x1,x2,且x10)恒成立求参数的取值范围.2.利用具体函数本身所具有的特征:如二次函数的图象被对称轴一分为二,可根据对称轴相对于所给单调区间的位置建立关于参数的关系式,解关系式求参数的取值范围.注意:若某个函数在区间[a,b]上是单调的,则该函数在此区间的任意非空子集上也是单调的.根据分段函数的单调性求参数时,一般从两方面考虑:一方面,每个分段区间上的函数具有相同的单调性,由此列出相关式子; 另一方面,要考虑分界点处函数值之间的大小关系,由此列出另外的式子,从而解得参数的取值范围.
已知函数y=f(x)是定义在R上的单调函数,A(0,2),B(2,-2)是其函数图象上的两点,则不等式|f(x-1)|>2的解集为(　D　)A.(1,3)　　　    B.(-∞,-3)∪(1,+∞)C.(-1,1)　　　    D.(-∞,1)∪(3,+∞)
思路点拨由题意可得f(0)=2,f(2)=-2,从而得出f(x)在R上为减函数,再根据不等式|f(x-1)|>2得出f(x-1)>f(0)或f(x-1)2,进而得出不等式的解集.
解析    由题意得f(0)=2,f(2)=-2.因为函数y=f(x)是定义在R上的单调函数,所以f(x)在R上为减函数.由|f(x-1)|>2,得f(x-1)>2或f(x-1)<-2,所以f(x-1)>f(0)或f(x-1)2,解得x<1或x>3.所以不等式|f(x-1)|>2的解集为(-∞,1)∪(3,+∞).
已知函数f(x)= 对于任意两个不相等的实数x1,x2∈R,都有不等式(x1-x2)[f(x1)-f(x2)]>0成立,则实数a的取值范围是 (　C　)A.[3,+∞)　    B.[0,3]C.[3,4]　     D.[2,4]
思路点拨由题意得f(x)在R上为单调递增函数.结合分段函数判断单调性的方法,讨论每段函数满足增函数时的条件及两段函数在分界点处函数值的关系,列关系式求解.
解析    因为对于任意两个不相等的实数x1,x2∈R,都有不等式(x1-x2)[f(x1)-f(x2)]>0成立,所以f(x)在R上为单调递增函数.y=|x2-2x-3|的图象如图所示: 因为f(x)在R上为单调递增函数,所以a≥3.当x0.在x=a处,需满足a2-2a-3≥a2-11,解得a≤4.综上,3≤a≤4.
3 | 求二次函数最值的常见类型及解法
1.求二次函数的最大(小)值有两种类型:一是函数定义域为实数集R,这时只要根据抛物线的开口方向,应用配方法即可求出最大(小)值;二是函数定义域为某一区间,这时二次函数的最大(小)值由它的单调性确定,而单调性又由抛物线的开口方向和对称轴的位置来决定,当开口方向或对称轴位置不确定时,需要进行分类讨论.2.求二次函数f(x)=ax2+bx+c(a>0)在区间[m,n]上的最值一般分为以下几种情况:(1)若- 在区间[m,n]内,则最小值为f ,最大值为f(m),f(n)中较大者;(2)若- n,则f(x)在区间[m,n]上单调递减,最大值为f(m),最小值为f(n).

相关课件更多