2022-2023年粤教版(2019)新教材高中物理选择性必修1 第2章机械振动本章整合课件

这是一份2022-2023年粤教版(2019)新教材高中物理选择性必修1 第2章机械振动本章整合课件，共23页。

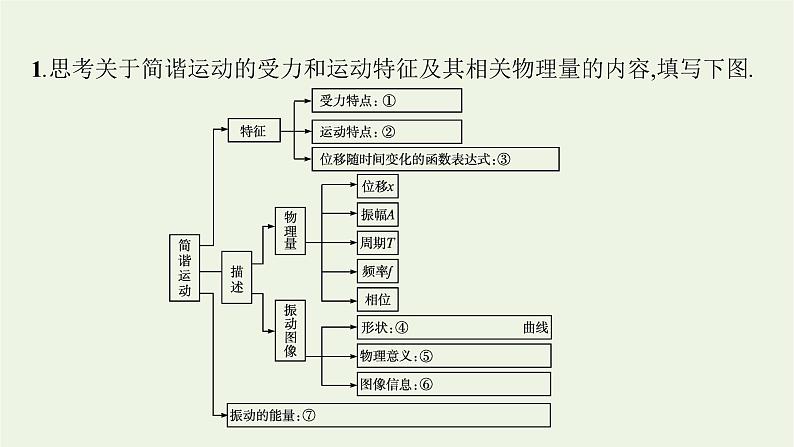
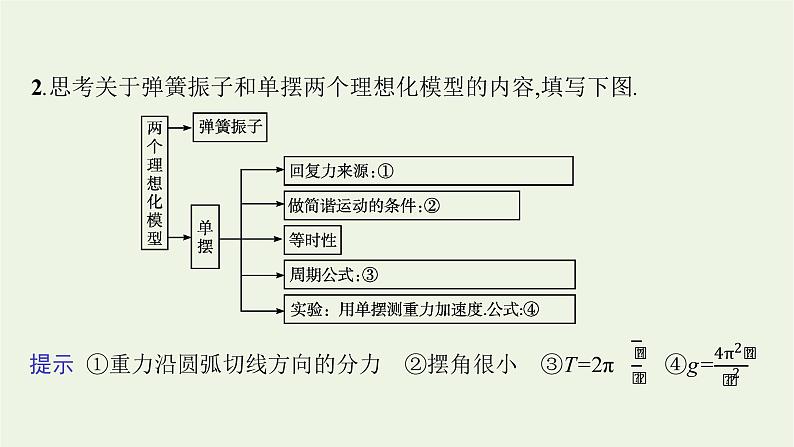
第二章知识网络体系构建本章知识可分为三部分:第一是简谐运动,主要是简谐运动的特征和基本物理量的描述;第二是两个理想化模型,即弹簧振子和单摆;第三是外力作用下的振动,包括阻尼振动和受迫振动.1.思考关于简谐运动的受力和运动特征及其相关物理量的内容,填写下图. 提示 ①F=-kx　②a=- (变加速运动)　③x=Acos(ωt+φ)　④正弦(或余弦)　⑤描述振动物体的位移随时间变化的规律　⑥振幅A、周期T、各时刻位移x　⑦动能与势能之和不变2.思考关于弹簧振子和单摆两个理想化模型的内容,填写下图. 3.思考阻尼振动和受迫振动的相关内容,填写下图. 提示 ①不断减小　②其他形式能　③周期性驱动力　④等于驱动力的频率　⑤f固重点题型归纳整合一、简谐运动与图像问题的综合例1一振子沿x轴做简谐运动,平衡位置在坐标原点,第一次把振子拉离平衡位置5 cm,从平衡位置向右开始计时时,振动图像如图所示,第二次把振子拉离平衡位置2 cm,也从振子从平衡位置向右开始计时,求第二次振子振动时:(1)位移为-1 cm的时刻;(2)发生2 cm位移的最大平均速度大小.解析 (1)从第一次振动可以看出弹簧振子的周期为T=4 s,弹簧振子的振动周期与振幅无关,故第二次振动周期也为T=4 s,第二次弹簧振子的振动方规律方法简谐运动的图像描述了振动质点的位移随时间变化的规律.从图像中可以确定位移、速度、加速度、动能和势能等物理量以及它们的变化规律,具体分析如下:变式训练1某质点的振动图像如图所示,下列说法正确的是(　　)A.1 s和3 s时刻,质点的速度相同B.1 s到2 s时间内,速度与加速度方向相同C.简谐运动的表达式为y=2sin(1.5πt+0.5π) cmD.简谐运动的表达式为y=2sin(0.5πt+0.5π) cm答案 D 解析 y-t图像上某点的切线的斜率表示速度,1 s和3 s时刻,质点的速度大小相等,方向相反,故A错误;1 s到2 s时间内,质点做减速运动,故加速度与速度反向,B错误;振幅为2 cm,周期为4 s,角速度为ω= =0.5π rad/s,故简谐运动的表达式为y=Asin(ωt+φ)=2sin(0.5πt+0.5π) cm,C错误,D正确.二、简谐运动的周期性和对称性例2一个质点在平衡位置O点的附近做简谐运动,它离开O点后经过3 s时间第一次经过M点,再经过2 s第二次经过M点,该质点再经过　　　　 s第三次经过M点.若该质点由O点出发在20 s内经过的路程是20 cm,则质点振动的振幅为　　　　 cm. 规律方法1.周期性做简谐运动的物体经过一个周期或几个周期后,能回复到原来的状态.2.对称性(1)速率的对称性:系统在关于平衡位置对称的两位置具有相等的速率.(2)加速度和回复力的对称性:系统在关于平衡位置对称的两位置具有等大反向的加速度和回复力.(3)时间的对称性:系统通过关于平衡位置对称的两段位移的时间相等.振动过程中通过任意两点A、B的时间与逆向通过此两点的时间相等.变式训练2弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从O、B间的P点以速度v向B点运动;在t=0.30 s时刻,振子速度第一次变为-v;在t=0.60 s时刻,振子速度第二次变为-v.(1)求弹簧振子的振动周期T.(2)若B、C之间的距离为20 cm,求振子在4.80 s内通过的路程.(3)若B、C之间的距离为20 cm,从P点以速度v向B点运动开始计时,写出弹簧振子简谐运动的方程.答案 (1)1.2 s　(2)160 cm 解析 (1)弹簧振子的振动周期T=(0.15+0.15)×4 s=1.2 s.(2)振子的振幅A= ×20 cm=10 cm振子4.80 s内通过的路程s=4×4A=4×4×10 cm=160 cm.