2022年黑龙江省齐齐哈尔市中考数学一模试卷（含解析）

2022年黑龙江省齐齐哈尔市中考数学一模试卷

副标题

一、选择题（本大题共10小题，共30.0分）

1. 的绝对值是

A.  B.  C.  D.

2. 汉字是中华民族智慧的结晶，是世界上独一无二的创造发明．在我们书写汉字的时候，能感受到汉字的演变之丰富，造型之奇美，内涵之厚重广博，其中有些汉字不乏对称之美，下列汉字中，是轴对称图形的为

A.  B.  C.  D.

3. 下列计算正确的是

A.  B.
C.  D.

4. 桥牌是体育活动项目之一，起源于西方，是一种扑克牌游戏．使用的扑克牌有黑桃、红心、方片、草花四种花色，每种花色张，共张．甲从一副洗均的桥牌中随机抽取一张，则抽出黑桃花色桥牌的概率是

A.  B.  C.  D.

5. 如图，一副三角板的一边重合，得到四边形，过点作直线，的度数为

A.
B.
C.
D.

6. 自“新冠肺炎”疫情以来，某地疫情日益严重，连续七天日确诊病例数为：，，，，，，单位：人，从数据中去掉一个最大值和一个最小值，剩下的个数据和原来的个数据相比，这两组数据一定不变的是

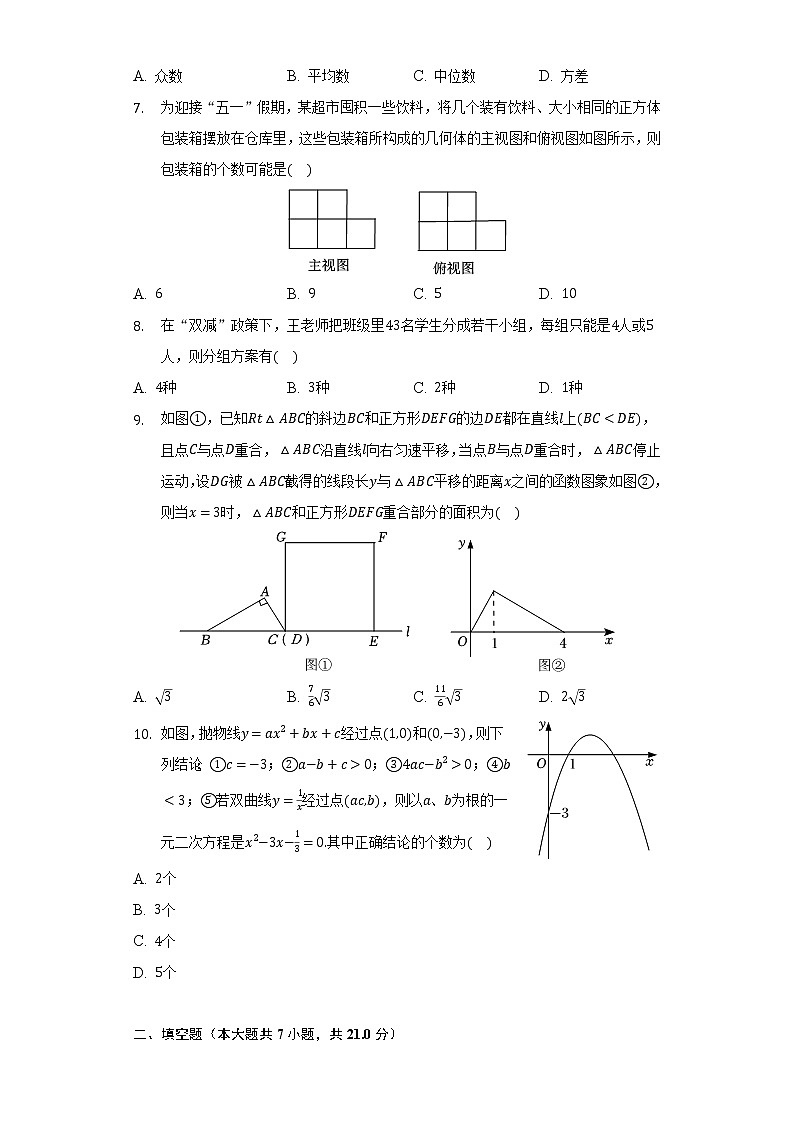
A. 众数 B. 平均数 C. 中位数 D. 方差

7. 为迎接“五一”假期，某超市囤积一些饮料，将几个装有饮料、大小相同的正方体包装箱摆放在仓库里，这些包装箱所构成的几何体的主视图和俯视图如图所示，则包装箱的个数可能是

A.  B.  C.  D.

8. 在“双减”政策下，王老师把班级里名学生分成若干小组，每组只能是人或人，则分组方案有

A. 种 B. 种 C. 种 D. 种

9. 如图，已知的斜边和正方形的边都在直线上，且点与点重合，沿直线向右匀速平移，当点与点重合时，停止运动，设被截得的线段长与平移的距离之间的函数图象如图，则当时，和正方形重合部分的面积为

A.  B.  C.  D.

10. 如图，抛物线经过点和，则下列结论：；；；；若双曲线经过点，则以、为根的一元二次方程是其中正确结论的个数为

A. 个
B. 个
C. 个
D. 个

二、填空题（本大题共7小题，共21.0分）

11. 根据实时统计数据，截至北京时间年月日时分，全球累计确诊新冠肺炎病例突破例．将用科学记数法表示为______．
12. 如图，点、在▱的对角线上，连接、、、，请添加一个条件使四边形是平行四边形，那么需要添加的条件是______只填一个即可
13. 用一块圆心角为的扇形铁皮，做一个圆锥形的烟囱帽接缝忽略不计，已知这块扇形铁皮的半径是，则此圆锥的高为______．
14. 若关于的分式方程无解，则______．
15. 如图，在平面直角坐标系中，菱形的边轴，垂足为，点在轴正半轴上，点的横坐标为，，若反比例函数的图象同时经过点、，则的值为______．

16. 菱形的边长为，对角线、交于点，，以为一边作正方形，过点作直线，垂足为，连接，则______．
17. 如图，在平面直角坐标系中，点在轴的正半轴上，且，以点为直角顶点，逆时针方向作，使；再以点为直角顶点，逆时针方向作，使；再以点为直角顶点，逆时针方向作，使；依次进行作下去，则点的坐标为______．

三、解答题（本大题共7小题，共69.0分）

18. 计算：；
    分解因式：．
    
    
    
    
    
    
     
19. 解方程：．
    
    
    
    
    
    
     
20. 年月，教育部印发关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见，某数学兴趣小组为了解本校七年级学生每周课外阅读的时间，随机调查了七年级部分学生，将收集的数据划分成组，并将结果绘制成两幅不完整的统计图，请你根据统计图的信息回答下列问题：

本次调查的样本容量为______，其中女生数量为______人；
将条形统计图补充完整；
扇形统计图中，______，课外阅读时间在组的扇形的圆心角度数是______；
若全校七年级共有学生人，则该校七年级每周课外阅读时间多于小时的学生约有多少人？






 

21. 如图，四边形，经过、、三点，为的直径，于点，且．
    证明：是的切线；
    若，，求图中阴影部分的面积．

22. 在新冠肺炎疫情期间，市派一辆货车将抗疫物资运往的市，途中因故障停留一段时间．一辆轿车沿同一条公路从市前往市，到达市停留一段时间后，原路原速返回．如图是两车距市的距离与货车行驶时间之间的函数图象，结合图象回答下列问题：
    图中的值是______；轿车的速度是______；
    求货车从市前往市的过程中，货车距市的距离与行驶时间之间的函数关系式；
    直接写出轿车出发多长时间与货车相距？

23. 综合与实践
    “手拉手”模型是初中几何图形的一种全等变形的重要模型，可以借助旋转和全等形的相关知识结合勾股定理等，来解决有关线段的长、角的度数等问题，在学习和生活中应用广泛，有着十分重要的地位和作用．
    某校数学活动小组进行了有关旋转的系列探究：
    如图，已知和均是等腰直角三角形，，且，，易证：，．
    深入探究：
    如图，将图中绕点逆时针旋转，连接、，并延长分别与、相交于点、，求证：，．
    解决问题：
    如图，将图中绕点逆时针旋转，使与重合，其他条件不变，若，，则______，______．
    拓展应用：
    如图，将图中绕点逆时针旋转，连接、，若，，，则______，______．
    提示：求时，可过点作于点

24. 综合与探究
    如图，在平面直角坐标系中，抛物线与轴交于，两点，与轴交于点，，，点是直线下方抛物线上的一个动点．过点作轴，交直线于点．
    求抛物线的解析式；
    若点是抛物线对称轴上的一个动点，则的最小值是______；
    求的最大值；
    在抛物线的对称轴上找点，使是以为斜边的直角三角形，请直接写出点的坐标．

答案和解析

1.【答案】
 

【解析】解：负数的绝对值等于它的相反数，
的绝对值是：．
故选：．
直接利用绝对值的定义得出答案．
此题主要考查了绝对值，正确掌握绝对值的定义是解题关键．
 

2.【答案】
 

【解析】解：选项A、、不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
选项D能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
故选：．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 

3.【答案】
 

【解析】解：、，故A不符合题意；
B、，故B不符合题意；
C、，故C符合题意；
D、与不属于同类项，不能合并，故D不符合题意；
故选：．
利用同底数幂的除法的法则，合并同类项的法则，同底数幂的乘法的法则，积的乘方的法则对各项进行运算即可．
本题主要考查同底数幂的除法，合并同类项，积的乘方，同底数幂的乘法，解答的关键是对相应的运算法则的掌握．
 

4.【答案】
 

【解析】解：一副扑克牌共张，其中黑桃张，
随机抽出一张牌得到黑桃的概率是；
故选D．
让黑桃的张数除以扑克牌的总张数即为所求的概率．
本题考查概率的求法，如果一个事件有种可能，而且这些事件的可能性相同，其中事件出现种结果，那么事件的概率．
 

5.【答案】
 

【解析】解：，
，
即，
，，，
，
故选：．
根据平行线的性质求解即可．
此题考查了平行线的性质，熟记平行线的性质定理是解题的关键．
 

6.【答案】
 

【解析】解：根据题意，从个数据中去掉一个最大值和一个最小值，剩下的个数据和原来的个数据相比，这两组数据一定不变的是中位数，
故选：．
根据平均数、中位数、众数、方差的意义即可求解．
本题考查了均数、中位数、众数、方差的意义，熟练掌握这四个概念的意义是解决本题的关键．
 

7.【答案】
 

【解析】解：结合主视图和俯视图可知，上层最多有个，最少个，下层一定有个，
故搭成这个几何体的小正方体包装箱的个数可能是个或个或个．
故选：．
易得这个几何体共有层，由俯视图可得第一层立方体的个数，由主视图可得第二层立方体的可能的个数，相加即可．
本题考查了学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．
 

8.【答案】
 

【解析】解：设可以分成组人组，组人组，
依题意得：，
．
又，均为自然数，
或，
共有种分组方案．
故选：．
设可以分成组人组，组人组，根据各组的人数之和为人，即可得出关于，的二元一次方程，结合，均为自然数，即可得出共有种分组方案．
本题考查了二元一次方程的应用，找准等量关系，正确列出二元一次方程是解题的关键．
 

9.【答案】
 

【解析】解：如图，过点作于点，

，
，
，
∽，
：：，
结合图图可知，当点和点重合时，被截得的线段长最长，即；
当点和点重合时，，
，
：：，即，
当时，，
，
设与的交点为，

则∽，
：：，
：：，即，
．
故选：．
过点作于点，由图形可知，当点和点重合时，被截得的线段长最长，即；当点和点重合时，，由此可解；画出当时的图形，利用相似可得出结论．
本题考查的是动点图象问题，涉及相似三角形的性质与判定，此类问题关键是得出和的长．
 

10.【答案】
 

【解析】解：抛物线经过点，
，故正确；
由图象可知，当时，，
，故错误；
抛物线与轴有两个交点，
，
，故错误；
抛物线经过点和，
，，
，
抛物线开口向下，
，
，故错误；
双曲线经过点，
，
，
，
，
以、为根的一元二次方程是，故正确；
故选：．
由抛物线经过点，即可判断；根据图象即可判断；根据抛物线经过点和，得出，，即可得出，由，即可判断；求得，即可判断．
本题考查了二次函数图象与系数的关系、二次函数图象上点的坐标特征，反比例函数图象上点的坐标特征，抛物线与轴的交点，解决本题的关键是综合运用二次函数的相关知识．
 

11.【答案】
 

【解析】解：．
故答案为：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数，当原数绝对值时，是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
 

12.【答案】
 

【解析】解：添加，
证明：四边形是平行四边形，
，，
，
，
，≌，
，
四边形是平行四边形．
故答案为：．
由平行四边形的性质得，，则，再证，≌，得，即可得出结论．
本题考查了平行四边形的判定与性质、全等三角形的判定与性质等知识，熟练掌握平行四边形的判定，证明≌是解题的关键．
 

13.【答案】
 

【解析】解：设圆锥的底面半径为，
根据题意得：，
解得：，
圆锥的高为，
故答案为：．
先求得圆锥的底面半径，然后利用勾股定理求得答案即可．
本题考查了圆锥的计算，解题的关键是首先求得圆锥的底面周长，利用圆锥的底面周长等于扇形的弧长求解．
 

14.【答案】或
 

【解析】解：关于的分式方程无解，
，
，
，
，
即，
当时，方程无解，
把代入中可得：，
故答案为：或．
由题意可得，由整式方程系数为时无解可求解值，再把代入整式方程中进行计算即可．
本题考查了分式方程的解，根据题意求出的值后再代入整式方程中进行计算是解题的关键．
 

15.【答案】
 

【解析】解：由题意得，，
在中，，
，
，
设点，则，
反比例函数的图象同时经过点、，
，
解得：，
，
故答案为：．
由点的横坐标为，可知菱形的边长为，利用勾股定理求出的长，表示的长，再设出点的纵坐标，表示点、的坐标，代入反比例函数关系式求出的值．
考查反比例函数图象上点的坐标特征、菱形的性质、勾股定理等知识，求出反比例函数图象上某个点的坐标是解决问题的关键．
 

16.【答案】或
 

【解析】解：在菱形中，，
菱形的边长为，且，
，
根据勾股定理，得，
点在线段上，如图所示：

在正方形中，，，
，
，
，
，
，
，
，
，
≌，
，
，
根据勾股定理，得，
点在线段的延长线上，如图所示：

同理可证≌，
，
，
，
根据勾股定理，得．
故答案为：或．
分两种情况：点在线段上，点在线段的延长线上，根据菱形的性质先求出，易证≌，可得，根据勾股定理即可求出．
本题考查了正方形的性质与菱形的性质，分情况讨论以及证明≌是解题的关键．
 

17.【答案】
 

【解析】解：由已知，点每次旋转转动，则转动一周需转动次，每次转动点到原点的距离变为转动前的倍，
，
点的在轴的负半轴上，
，
故答案为：
本题点坐标变化规律要分别从旋转次数与点所在象限或坐标轴、点到原点的距离与旋转次数的对应关系．
本题是平面直角坐标系下的规律探究题，除了研究动点变化的相关数据规律，还应该注意各个象限内点的坐标符号．
 

18.【答案】解：原式

；
原式
．
 

【解析】先根据二次根式的性质、负整数指数幂、特殊角的三角函数值和绝对值的意义计算，然后合并即可；
先提公因式，然后利用平方差公式分解．
本题考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的乘法法则、负整数指数幂和特殊角的三角函数值是解决问题的关键．也考查了因式分解．
 

19.【答案】解：方程化为：，
，
或，
所以，．
 

【解析】先把方程化为一般式，然后利用因式分解法解方程．
本题考查了解一元二次方程因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
 

20.【答案】     
 

【解析】解：本次调查的样本容量为：；女生数量为：人，
故答案为：；；
组男生数量为：人，
补全条形统计图如下：


，课外阅读时间在组的扇形的圆心角度数是，
故答案为：；；
人，
答：该校七年级每周课外阅读时间多于小时的学生约有人．
由组的人数除以占的百分比得到调查总人数；把各组女生人数相加即可得出女生数量；
用男生数量分别减去其它三组男生人数即可得出组男生数量，即可将条形统计图补充完整；
用组人数除以总人数即可得出的值，用乘组所占比例即可得出组的扇形的圆心角度数；
根据等级、与的百分比之和乘以即可得到结果．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
 

21.【答案】证明：连接，，
，
，
，
，
，
，
，
是的半径，
是的切线；
解：为的直径，
，
在中，
，
，
，
，
是等边三角形，
，
，，
，
，
是的中点，
是的中点，
是的中位线，
，
，，
则．
 

【解析】连接，根据等腰三角形的性质和直角三角形的性质证得，根据切线的判定即可证得是的切线；
在中，解直角三角形求出，再证得，是等边三角形，根据，由三角形和扇形的面积公式即可求出结果．
本题主要考查了切线的判定，圆周角定理，扇形的面积公式，垂径定理，解直角三角形，三角形中位线定理，解题的关键：正确作出辅助线；证出是等边三角形．
 

22.【答案】 
 

【解析】解：由图象得，；
轿车的速度为：；
故答案为：；；
设线段所在直线的解析式为，
图象经过点和点，
，
解得，
；
；
设所在直线解析式为，
图象经过点和点，
，
解得，
，
；
桥车从市前往市时，
货车出故障前的速度为：，
设轿车出发小时与货车相距，
根据题意，得或，
解得或；
桥车从市返回市时，
货车出故障后的速度为：，
设轿车出发小时与货车相距，
根据题意，得，
解得：．
答：轿车出发小时或小时或与货车相距．
由图象可知轿车从地前往地用时为小时，据此可得的值以及轿车的速度；
分段函数，线段与线段的函数关系式利用待定系数法求解即可；
根据两车的速度分桥车从市前往市时和桥车从市返回市时两种情况列方程解答即可．
本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
 

23.【答案】   
 

【解析】证明：，
，
，
在与中，
，
≌，
，，
，，
，
，
，
，
即，；
解：同理可证：≌，
，，，
，
，，，
，
，
∽，
，
，
，
；
故答案为：；；
解：如图所示：过点作于，

，
，
，
，
，
，
，
，
，
，，
，，
，
，
同理可证≌，
．
故答案为：；．
根据证明与全等，进而利用全等三角形的性质和垂直的定义解得即可；
同理可证与全等，根据全等三角形的性质和勾股定理解得即可；
过点作于，根据勾股定理得出，进而利用全等三角形的判定和性质解得即可．
本题属于几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形或相似三角形解决问题，属于中考压轴题．
 

24.【答案】
 

【解析】解：，，
，，
，，
将点、代入，
，
解得，
；
，
抛物线的对称轴为直线，
点与点关于对称轴对称，
，
直线与对称轴的交点即为点，
令，则，
，
，
的最小值是；
设直线的解析式为，
，
解得，
，
设，则，
，
当时，有最大值；
设，
设的中点为，则，
为的斜边，
，
，
或，
或．
求出、点坐标，将点、代入，即可求解；
由点与点关于对称轴对称，则，直线与对称轴的交点即为点，即为所求最短距离；
先求直线的解析式，设，则，，当时，有最大值；
设，设的中点为，则，由题意可知，求出的值即可求解．
本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，利用直角三角形的性质，建立方程求点的坐标，利用抛物线的对称性求最短距离是解题的关键．