
江苏省盐都区2021-2022学年中考数学押题卷含解析
展开2021-2022中考数学模拟试卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.在同一直角坐标系中,二次函数y=x2与反比例函数y=(x>0)的图象如图所示,若两个函数图象上有三个不同的点A(x1,m),B(x2,m),C(x3,m),其中m为常数,令ω=x1+x2+x3,则ω的值为( )
A.1 B.m C.m2 D.
2.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点E是△ABC的内心,过点E作EF∥AB交AC于点F,则EF的长为( )
A. B. C. D.
3.若点A(2,),B(-3,),C(-1,)三点在抛物线的图象上,则、、的大小关系是( )
A.
B.
C.
D.
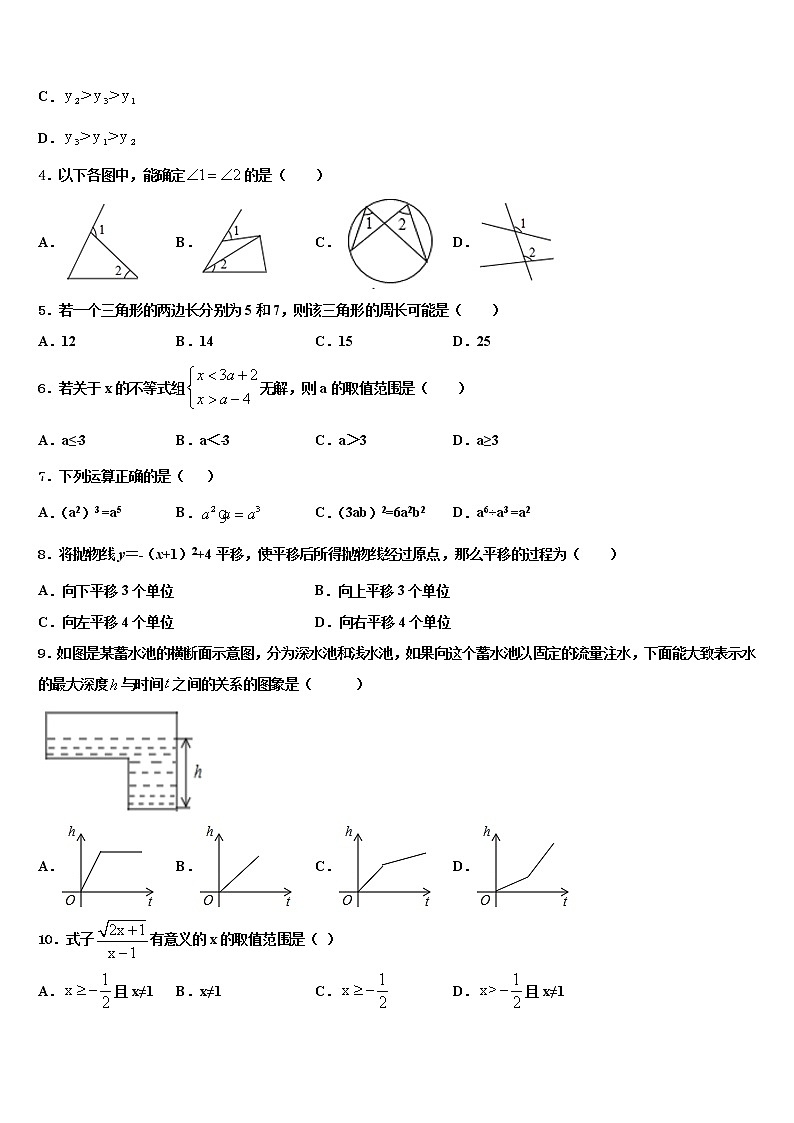
4.以下各图中,能确定的是( )
A. B. C. D.
5.若一个三角形的两边长分别为5和7,则该三角形的周长可能是( )
A.12 B.14 C.15 D.25
6.若关于x的不等式组无解,则a的取值范围是( )
A.a≤﹣3 B.a<﹣3 C.a>3 D.a≥3
7.下列运算正确的是( )
A.(a2)3 =a5 B. C.(3ab)2=6a2b2 D.a6÷a3 =a2
8.将抛物线y=﹣(x+1)2+4平移,使平移后所得抛物线经过原点,那么平移的过程为( )
A.向下平移3个单位 B.向上平移3个单位
C.向左平移4个单位 D.向右平移4个单位
9.如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果向这个蓄水池以固定的流量注水,下面能大致表示水的最大深度与时间之间的关系的图象是( )
A. B. C. D.
10.式子有意义的x的取值范围是( )
A.且x≠1 B.x≠1 C. D.且x≠1
11.在-,,0,-2这四个数中,最小的数是( )
A. B. C.0 D.-2
12.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B.30sinα米 C.30tanα米 D.30cosα米
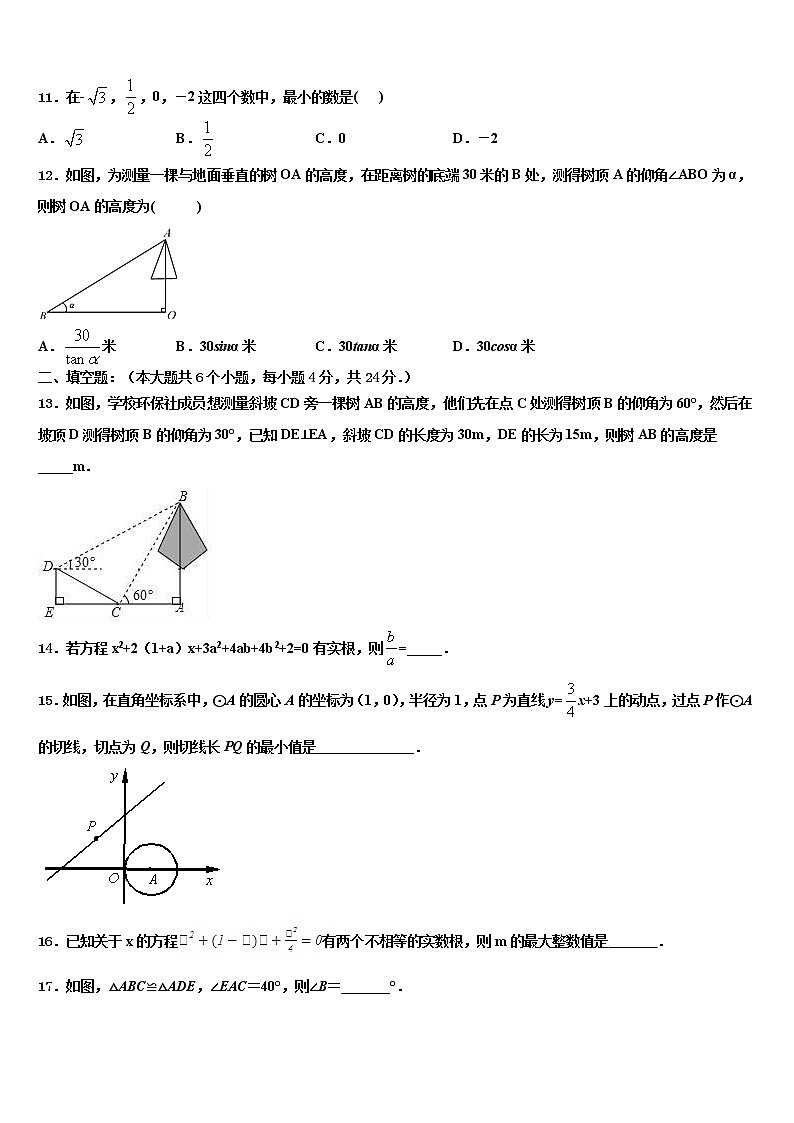
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知DE⊥EA,斜坡CD的长度为30m,DE的长为15m,则树AB的高度是_____m.
14.若方程x2+2(1+a)x+3a2+4ab+4b2+2=0有实根,则=_____.
15.如图,在直角坐标系中,⊙A的圆心A的坐标为(1,0),半径为1,点P为直线y=x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是______________.
16.已知关于x的方程有两个不相等的实数根,则m的最大整数值是 .
17.如图,△ABC≌△ADE,∠EAC=40°,则∠B=_______°.
18.已知关于x的一元二次方程mx2+5x+m2﹣2m=0有一个根为0,则m=_____.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19.(6分)如图,二次函数y=x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).求二次函数的解析式;求函数图象的顶点坐标及D点的坐标;二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
20.(6分)如图,矩形中,点是线段上一动点, 为的中点, 的延长线交BC于.
(1)求证: ;
(2)若,,从点出发,以l的速度向运动(不与重合).设点运动时间为,请用表示的长;并求为何值时,四边形是菱形.
21.(6分)请根据图中提供的信息,回答下列问题:
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和n(n>10,且n为整数)个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
22.(8分)如图,抛物线与x轴交于点A,B,与轴交于点C,过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD,已知点A坐标为(-1,0).
求该抛物线的解析式;求梯形COBD的面积.
23.(8分)如图,在平行四边形ABCD中,连接AC,做△ABC的外接圆⊙O,延长EC交⊙O于点D,连接BD、AD,BC与AD交于点F分,∠ABC=∠ADB。
(1)求证:AE是⊙O的切线;
(2)若AE=12,CD=10,求⊙O的半径。
24.(10分)(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:
根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
25.(10分)如图,有四张背面完全相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A,B,C,D表示).
26.(12分)如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)求证:△ABF≌△EDF;
(2)若AB=6,BC=8,求AF的长.
27.(12分)如图,AB是⊙O的直径,D、D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF.
(1)求证:CE是⊙O的切线;
(2)连接CD、CB,若AD=CD=a,求四边形ABCD面积.
参考答案
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、D
【解析】
本题主要考察二次函数与反比例函数的图像和性质.
【详解】
令二次函数中y=m.即x2=m,解得x=或x=令反比例函数中y=m,即=m,解得x=,将x的三个值相加得到ω=+()+=.所以本题选择D.
【点睛】
巧妙借助三点纵坐标相同的条件建立起两个函数之间的联系,从而解答.
2、A
【解析】
过E作EG∥AB,交AC于G,易得CG=EG,EF=AF,依据△ABC∽△GEF,即可得到EG:EF:GF,根据斜边的长列方程即可得到结论.
【详解】
过E作EG∥BC,交AC于G,则∠BCE=∠CEG.
∵CE平分∠BCA,∴∠BCE=∠ACE,∴∠ACE=∠CEG,∴CG=EG,同理可得:EF=AF.
∵BC∥GE,AB∥EF,∴∠BCA=∠EGF,∠BAC=∠EFG,∴△ABC∽△GEF.
∵∠ABC=90°,AB=6,BC=8,∴AC=10,∴EG:EF:GF=BC:BC:AC=4:3:5,设EG=4k=AG,则EF=3k=CF,FG=5k.
∵AC=10,∴3k+5k+4k=10,∴k=,∴EF=3k=.
故选A.
【点睛】
本题考查了相似三角形的判定与性质,等腰三角形的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构相似三角形以及构造等腰三角形.
3、C
【解析】
首先求出二次函数的图象的对称轴x==2,且由a=1>0,可知其开口向上,然后由A(2,)中x=2,知最小,再由B(-3,),C(-1,)都在对称轴的左侧,而在对称轴的左侧,y随x得增大而减小,所以.总结可得.
故选C.
点睛:此题主要考查了二次函数的图像与性质,解答此题的关键是(1)找到二次函数的对称轴;(2)掌握二次函数的图象性质.
4、C
【解析】
逐一对选项进行分析即可得出答案.
【详解】
A中,利用三角形外角的性质可知,故该选项错误;
B中,不能确定的大小关系,故该选项错误;
C中,因为同弧所对的圆周角相等,所以,故该选项正确;
D中,两直线不平行,所以,故该选项错误.
故选:C.
【点睛】
本题主要考查平行线的性质及圆周角定理的推论,掌握圆周角定理的推论是解题的关键.
5、C
【解析】
先根据三角形三条边的关系求出第三条边的取值范围,进而求出周长的取值范围,从而可的求出符合题意的选项.
【详解】
∴三角形的两边长分别为5和7,
∴2<第三条边<12,
∴5+7+2<三角形的周长<5+7+12,
即14<三角形的周长<24,
故选C.
【点睛】
本题考查了三角形三条边的关系:三角形任意两边之和大于第三边,任意两边之差小于第三边,据此解答即可.
6、A
【解析】
【分析】利用不等式组取解集的方法,根据不等式组无解求出a的取值范围即可.
【详解】∵不等式组无解,
∴a﹣4≥3a+2,
解得:a≤﹣3,
故选A.
【点睛】本题考查了一元一次不等式组的解集,熟知一元一次不等式组的解集的确定方法“同大取大、同小取小、大小小大中间找、大大小小无处找”是解题的关键.
7、B
【解析】
分析:本题考察幂的乘方,同底数幂的乘法,积的乘方和同底数幂的除法.
解析: ,故A选项错误; a3·a = a4故B选项正确;(3ab)2 = 9a2b2故C选项错误; a6÷a3 = a3故D选项错误.
故选B.
8、A
【解析】
将抛物线平移,使平移后所得抛物线经过原点,
若左右平移n个单位得到,则平移后的解析式为:,将(0,0)代入后解得:n=-3或n=1,所以向左平移1个单位或向右平移3个单位后抛物线经过原点;
若上下平移m个单位得到,则平移后的解析式为:,将(0,0)代入后解得:m=-3,所以向下平移3个单位后抛物线经过原点,
故选A.
9、C
【解析】
首先看图可知,蓄水池的下部分比上部分的体积小,故h与t的关系变为先快后慢.
【详解】
根据题意和图形的形状,可知水的最大深度h与时间t之间的关系分为两段,先快后慢。
故选:C.
【点睛】
此题考查函数的图象,解题关键在于观察图形
10、A
【解析】
根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使在实数范围内有意义,必须且.故选A.
11、D
【解析】
根据正数大于0,负数小于0,正数大于一切负数,两个负数,绝对值大的反而小比较即可.
【详解】
在﹣,,0,﹣1这四个数中,﹣1<﹣<0<,
故最小的数为:﹣1.
故选D.
【点睛】
本题考查了实数的大小比较,解答本题的关键是熟练掌握实数的大小比较方法,特别是两个负数的大小比较.
12、C
【解析】
试题解析:在Rt△ABO中,
∵BO=30米,∠ABO为α,
∴AO=BOtanα=30tanα(米).
故选C.
考点:解直角三角形的应用-仰角俯角问题.
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13、1
【解析】
先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
【详解】
解:作DF⊥AB于F,交BC于G.则四边形DEAF是矩形,
∴DE=AF=15m,
∵DF∥AE,
∴∠BGF=∠BCA=60°,
∵∠BGF=∠GDB+∠GBD=60°,∠GDB=30°,
∴∠GDB=∠GBD=30°,
∴GD=GB,
在Rt△DCE中,∵CD=2DE,
∴∠DCE=30°,
∴∠DCB=90°,
∵∠DGC=∠BGF,∠DCG=∠BFG=90°
∴△DGC≌△BGF,
∴BF=DC=30m,
∴AB=30+15=1(m),
故答案为1.
【点睛】
本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.
14、
【解析】
因为方程有实根,所以△≥0,配方整理得(a+2b)2+(a﹣1)2≤0,再利用非负性求出a,b的值即可.
【详解】
∵方程有实根,
∴△≥0,即△=4(1+a)2﹣4(3a2+4ab+4b2+2)≥0,
化简得:2a2+4ab+4b2﹣2a+1≤0,
∴(a+2b)2+(a﹣1)2≤0,而(a+2b)2+(a﹣1)2≥0,
∴a+2b=0,a﹣1=0,解得a=1,b=﹣,
∴=﹣.
故答案为﹣.
15、2
【解析】
分析:因为BP=,AB的长不变,当PA最小时切线长PB最小,所以点P是过点A向直线l所作垂线的垂足,利用△APC≌△DOC求出AP的长即可求解.
详解:如图,作AP⊥直线y=x+3,垂足为P,此时切线长PB最小,设直线与x轴,y轴分别交于D,C.
∵A的坐标为(1,0),∴D(0,3),C(﹣4,0),∴OD=3,AC=5,
∴DC==5,∴AC=DC,
在△APC与△DOC中,
∠APC=∠COD=90°,∠ACP=∠DCO,AC=DC,
∴△APC≌△DOC,∴AP=OD=3,
∴PB==2.
故答案为2.
点睛:本题考查了切线的性质,全等三角形的判定性质,勾股定理及垂线段最短,因为直角三角形中的三边长满足勾股定理,所以当其中的一边的长不变时,即可根据另一边的取值情况确定第三边的最大值或最小值.
16、1.
【解析】
试题分析:∵关于x的方程有两个不相等的实数根,
∴.
∴m的最大整数值为1.
考点:1.一元二次方程根的判别式;2.解一元一次不等式.
17、1°
【解析】
根据全等三角形的对应边相等、对应角相等得到∠BAC=∠DAE,AB=AD,根据等腰三角形的性质和三角形内角和定理计算即可.
【详解】
∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,
∴∠BAD=∠EAC=40°,
∴∠B=(180°-40°)÷2=1°,
故答案为1.
【点睛】
本题考查的是全等三角形的性质和三角形内角和定理,掌握全等三角形的对应边相等、对应角相等是解题的关键.
18、1
【解析】
【分析】根据一元二次方程的定义以及一元二次方程的解的定义列出关于m的方程,通过解关于m的方程求得m的值即可.
【详解】∵关于x的一元二次方程mx1+5x+m1﹣1m=0有一个根为0,
∴m1﹣1m=0且m≠0,
解得,m=1,
故答案是:1.
【点睛】本题考查了一元二次方程ax1+bx+c=0(a≠0)的解的定义.解答该题时需注意二次项系数a≠0这一条件.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19、(1)y=x1﹣4x+6;(1)D点的坐标为(6,0);(3)存在.当点C的坐标为(4,1)时,△CBD的周长最小
【解析】
(1)只需运用待定系数法就可求出二次函数的解析式;
(1)只需运用配方法就可求出抛物线的顶点坐标,只需令y=0就可求出点D的坐标;
(3)连接CA,由于BD是定值,使得△CBD的周长最小,只需CD+CB最小,根据抛物线是轴对称图形可得CA=CD,只需CA+CB最小,根据“两点之间,线段最短”可得:当点A、C、B三点共线时,CA+CB最小,只需用待定系数法求出直线AB的解析式,就可得到点C的坐标.
【详解】
(1)把A(1,0),B(8,6)代入,得
解得:
∴二次函数的解析式为;
(1)由,得
二次函数图象的顶点坐标为(4,﹣1).
令y=0,得,
解得:x1=1,x1=6,
∴D点的坐标为(6,0);
(3)二次函数的对称轴上存在一点C,使得的周长最小.
连接CA,如图,
∵点C在二次函数的对称轴x=4上,
∴xC=4,CA=CD,
∴的周长=CD+CB+BD=CA+CB+BD,
根据“两点之间,线段最短”,可得
当点A、C、B三点共线时,CA+CB最小,
此时,由于BD是定值,因此的周长最小.
设直线AB的解析式为y=mx+n,
把A(1,0)、B(8,6)代入y=mx+n,得
解得:
∴直线AB的解析式为y=x﹣1.
当x=4时,y=4﹣1=1,
∴当二次函数的对称轴上点C的坐标为(4,1)时,的周长最小.
【点睛】
本题考查了(1)二次函数综合题;(1)待定系数法求一次函数解析式;(3)二次函数的性质;(4)待定系数法求二次函数解析式;(5)线段的性质:(6)两点之间线段最短.
20、 (1)证明见解析;(2) PD=8-t,运动时间为秒时,四边形PBQD是菱形.
【解析】
(1)先根据四边形ABCD是矩形,得出AD∥BC,∠PDO=∠QBO,再根据O为BD的中点得出△POD≌△QOB,即可证得OP=OQ;
(2)根据已知条件得出∠A的度数,再根据AD=8cm,AB=6cm,得出BD和OD的长,再根据四边形PBQD是菱形时,利用勾股定理即可求出t的值,判断出四边形PBQD是菱形.
【详解】
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
又∵O为BD的中点,
∴OB=OD,
在△POD与△QOB中,
,
∴△POD≌△QOB,
∴OP=OQ;
(2)PD=8-t,
∵四边形PBQD是菱形,
∴BP=PD= 8-t,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即62+t2=(8-t)2,
解得:t=,
即运动时间为秒时,四边形PBQD是菱形.
【点睛】
本题考查了矩形的性质,菱形的性质,全等三角形的判定与性质,勾股定理等,熟练掌握相关知识是解题关键.注意数形结合思想的运用.
21、(1)一个水瓶40元,一个水杯是8元;(2)当10<n<25时,选择乙商场购买更合算.当n>25时,选择甲商场购买更合算.
【解析】
(1)设一个水瓶x元,表示出一个水杯为(48﹣x)元,根据题意列出方程,求出方程的解即可得到结果;
(2)计算出两商场得费用,比较即可得到结果.
【详解】
解:(1)设一个水瓶x元,表示出一个水杯为(48﹣x)元,
根据题意得:3x+4(48﹣x)=152,
解得:x=40,
则一个水瓶40元,一个水杯是8元;
(2)甲商场所需费用为(40×5+8n)×80%=160+6.4n
乙商场所需费用为5×40+(n﹣5×2)×8=120+8n
则∵n>10,且n为整数,
∴160+6.4n﹣(120+8n)=40﹣1.6n
讨论:当10<n<25时,40﹣1.6n>0,160+0.64n>120+8n,
∴选择乙商场购买更合算.
当n>25时,40﹣1.6n<0,即 160+0.64n<120+8n,
∴选择甲商场购买更合算.
【点睛】
此题主要考查不等式的应用,解题的关键是根据题意找到等量关系与不等关系进行列式求解.
22、(1)(2)
【解析】
(1)将A坐标代入抛物线解析式,求出a的值,即可确定出解析式.
(2)抛物线解析式令x=0求出y的值,求出OC的长,根据对称轴求出CD的长,令y=0求出x的值,确定出OB的长,根据梯形面积公式即可求出梯形COBD的面积.
【详解】
(1)将A(―1,0)代入中,得:0=4a+4,解得:a=-1.
∴该抛物线解析式为.
(2)对于抛物线解析式,令x=0,得到y=2,即OC=2,
∵抛物线的对称轴为直线x=1,∴CD=1.
∵A(-1,0),∴B(2,0),即OB=2.
∴.
23、(1)证明见解析;(2).
【解析】
(1)作辅助线,先根据垂径定理得:OA⊥BC,再证明OA⊥AE,则AE是⊙O的切线;
(2)连接OC,证明△ACE∽△DAE,得,计算CE的长,设⊙O的半径为r,根据勾股定理得:r2=62+(r-2)2,解出可得结论.
【详解】
(1)证明:连接OA,交BC于G,
∵∠ABC=∠ADB.∠ABC=∠ADE,
∴∠ADB=∠ADE,
∴,
∴OA⊥BC,
∵四边形ABCE是平行四边形,
∴AE∥BC,
∴OA⊥AE,
∴AE是⊙O的切线;
(2)连接OC,
∵AB=AC=CE,
∴∠CAE=∠E,
∵四边形ABCE是平行四边形,
∴BC∥AE,∠ABC=∠E,
∴∠ADC=∠ABC=∠E,
∴△ACE∽△DAE,,
∵AE=12,CD=10,
∴AE2=DE•CE,
144=(10+CE)CE,
解得:CE=8或-18(舍),
∴AC=CE=8,
∴Rt△AGC中,AG==2,
设⊙O的半径为r,
由勾股定理得:r2=62+(r-2)2,
r=,
则⊙O的半径是.
【点睛】
此题考查了垂径定理,圆周角定理,相似三角形的判定与性质,切线的判定与性质,熟练掌握各自的判定与性质是解本题的关键.
24、(1)100;(2)作图见解析;(3)1.
【解析】
试题分析:(1)根据百分比= 计算即可;
(2)求出“打球”和“其他”的人数,画出条形图即可;
(3)用样本估计总体的思想解决问题即可.
试题解析:(1)本次抽样调查中的样本容量=30÷30%=100,
故答案为100;
(2)其他有100×10%=10人,打球有100﹣30﹣20﹣10=40人,条形图如图所示:
(3)估计该校课余兴趣爱好为“打球”的学生人数为2000×40%=1人.
25、(1).(2)公平.
【解析】
试题分析:(1)首先根据题意结合概率公式可得答案;
(2)首先根据(1)求得摸出两张牌面图形都是轴对称图形的有16种情况,若摸出两张牌面图形都是中心对称图形的有12种情况,继而求得小明赢与小亮赢的概率,比较概率的大小,即可知这个游戏是否公平.
试题解析:(1)共有4张牌,正面是中心对称图形的情况有3种,所以摸到正面是中心对称图形的纸牌的概率是;
(2)列表得:
| A | B | C | D |
A |
| (A,B) | (A,C) | (A,D) |
B | (B,A) |
| (B,C) | (B,D) |
C | (C,A) | (C,B) |
| (C,D) |
D | (D,A) | (D,B) | (D,C) |
|
共产生12种结果,每种结果出现的可能性相同,其中两张牌都是轴对称图形的有6种,
∴P(两张都是轴对称图形)=,因此这个游戏公平.
考点:游戏公平性;轴对称图形;中心对称图形;概率公式;列表法与树状图法.
26、(1)见解析;(2)
【解析】
(1)根据矩形的性质可得AB=CD,∠C=∠A=90°,再根据折叠的性质可得DE=CD,∠C=∠E=90°,然后利用“角角边”证明即可;
(2)设AF=x,则BF=DF=8-x,根据勾股定理列方程求解即可.
【详解】
(1)证明:在矩形ABCD中,AB=CD,∠A=∠C=90°,
由折叠得:DE=CD,∠C=∠E=90°,
∴AB=DE,∠A=∠E=90°,
∵∠AFB=∠EFD,
∴△ABF≌△EDF(AAS);
(2)解:∵△ABF≌△EDF,
∴BF=DF,
设AF=x,则BF=DF=8﹣x,
在Rt△ABF中,由勾股定理得:
BF2=AB2+AF2,即(8﹣x)2=x2+62,
x=,即AF=
【点睛】
本题考查了翻折变换的性质,全等三角形的判定与性质,矩形的性质,勾股定理,翻折前后对应边相等,对应角相等,利用勾股定理列出方程是解题的关键.
27、(1)证明见解析;(2)
【解析】
(1)连接OC,AC,可先证明AC平分∠BAE,结合圆的性质可证明OC∥AE,可得∠OCB=90°,可证得结论;
(2)可先证得四边形AOCD为平行四边形,再证明△OCB为等边三角形,可求得CF、AB,利用梯形的面积公式可求得答案.
【详解】
(1)证明:连接OC,AC.
∵CF⊥AB,CE⊥AD,且CE=CF.
∴∠CAE=∠CAB.
∵OC=OA,
∴∠CAB=∠OCA.
∴∠CAE=∠OCA.
∴OC∥AE.
∴∠OCE+∠AEC=180°,
∵∠AEC=90°,
∴∠OCE=90°即OC⊥CE,
∵OC是⊙O的半径,点C为半径外端,
∴CE是⊙O的切线.
(2)解:∵AD=CD,
∴∠DAC=∠DCA=∠CAB,
∴DC∥AB,
∵∠CAE=∠OCA,
∴OC∥AD,
∴四边形AOCD是平行四边形,
∴OC=AD=a,AB=2a,
∵∠CAE=∠CAB,
∴CD=CB=a,
∴CB=OC=OB,
∴△OCB是等边三角形,
在Rt△CFB中,CF= ,
∴S四边形ABCD= (DC+AB)•CF=
【点睛】
本题主要考查切线的判定,掌握切线的两种判定方法是解题的关键,即有切点时连接圆心和切点,然后证明垂直,没有切点时,过圆心作垂直,证明圆心到直线的距离等于半径.
江苏省无锡市2021-2022学年中考数学押题卷含解析: 这是一份江苏省无锡市2021-2022学年中考数学押题卷含解析,共23页。试卷主要包含了如图,直线与y轴交于点等内容,欢迎下载使用。
江苏省邳州市市级名校2021-2022学年中考数学押题卷含解析: 这是一份江苏省邳州市市级名校2021-2022学年中考数学押题卷含解析,共23页。试卷主要包含了八边形的内角和为,一、单选题,已知抛物线y=等内容,欢迎下载使用。
2021-2022学年江苏省徐州市名校中考数学押题卷含解析: 这是一份2021-2022学年江苏省徐州市名校中考数学押题卷含解析,共21页。试卷主要包含了如图,与∠1是内错角的是,八边形的内角和为等内容,欢迎下载使用。













