江苏省无锡市锡山区锡东片2021-2022学年八年级下学期期中考试数学试卷（含答案）

2021—2022学年第二学期期中试卷

初二数学     2022.4

注意：（1）本试卷分试题和答题卡两部分，所有答案一律写在答题卡上．

（2）考试时间为100分钟，试卷满分130分．

一、选择题（本大题共10小题，每小题3分，共30分）

1．在下列四个图案中，不是中心对称图形的是----------------------------------（ ▲ ）

A．             B．                 C．                 D．

2．下列各式：，其中分式共有-----------------（ ▲ ）

A．4个         B．3个            C．2个            D．1个

3．如果分式  的值为0，那么x为-----------------------------------------（ ▲ ）

A．－2　　　  　B．0　　  　　      C．1　　　        　D．2

4．下列事件是必然事件的是----------------------------------------------（ ▲ ）

A．明天天晴；

B．在2022年出生的367名儿童中，至少有两人的生日是同一天；

C．打开电视机，正在播放关于‘俄乌战事’；

D．买彩票中奖．

5．要想了解10万名考生的数学成绩，从中抽取了2000名考生的数学成绩进行统计分析，以下说法正确的是------------------------------------------------------（ ▲ ）

A．这2000名考生是总体的一个样本     B．每位考生的数学成绩是个体

C．10万名考生是总体                 D．2000名考生是样本的容量

6．下列命题中，正确的是----------------------------------------------------（ ▲ ）

A．对角线相等的四边形是矩形  

B．一组对边平行，一组对边相等的四边形是平行四边形

C．对角线互相垂直且相等的四边形是正方形     

D．菱形的对角线互相平分

7．某市政府决定对城区580 公顷的绿化带进行一次全面的绿化改造，实际每天绿化改造的面积比原计划多10 公顷，结果提前7天完成绿化改造任务。若设原计划每天绿化面积是x公顷，根据题意下列方程正确的是---------------------------------------（ ▲ ）

 A．               B．

 C．               D．

8．如图在矩形纸片中，，点在边上，将沿直线折叠，点恰好落在对角线上的点处，若，则的长是--（ ▲ ）

A．3           B． 6            C． 4             D．5

9．已知四个点A（－8，0）、B（0，6）、C（4a，3a）、D能组成平行四边形，则CD的最小值为-------------------------------------------------------------------（ ▲ ）

A． 5              B．10            C．             D．

10．如图，正方形ABCO和正方形DEFO的顶点A，O，E在同一直线l上，且EF＝，AB＝2，给出下列结论：①∠COD＝45°；②AD⊥CF；③CF＝BD＝；④四边形ABDO的面积与正方形ABCO的面积相等．其中正确的结论为----------------------（ ▲ ）

A．①②④           B．①②        C．①②③        D．①③④

第8题                               第10题

二、填空题 (本大题共8小题，每小题2分，共16分)

11．函数中，自变量x的取值范围是   ▲   ．

12．若菱形的两条对角线分别为2和3，则此菱形的面积是   ▲   ．

13．一个袋中装有6个红球，3个黄球，1个白球，每个球除颜色外都相同，任意摸出一球，摸到黄球的概率为   ▲   ．

14．在□ABCD中，若∠A：∠B＝1：2，则∠C＝   ▲   °．

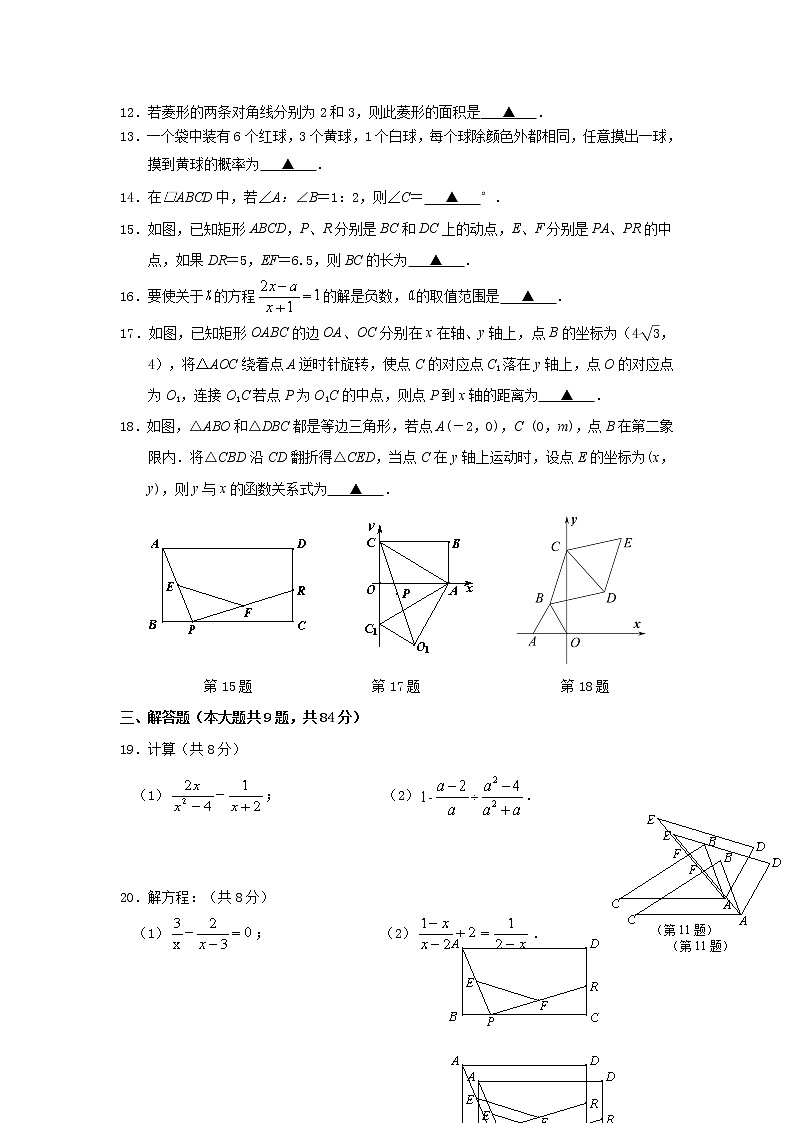
15．如图，已知矩形ABCD，P、R分别是BC和DC上的动点，E、F分别是PA、PR的中点，如果DR＝5，EF＝6.5，则BC的长为   ▲   ．

16．要使关于的方程的解是负数，的取值范围是   ▲   ．

17．如图，已知矩形OABC的边OA、OC分别在x在轴、y轴上，点B的坐标为（4，4），将△AOC绕着点A逆时针旋转，使点C的对应点C1落在y轴上，点O的对应点为O1，连接O1C若点P为O1C的中点，则点P到x轴的距离为   ▲   ．

18．如图，△ABO和△DBC都是等边三角形，若点A(－2，0)，C (0，m)，点B在第二象限内．将△CBD沿CD翻折得△CED，当点C在y轴上运动时，设点E的坐标为(x，y)，则y与x的函数关系式为   ▲   ．

第15题                 第17题                    第18题

三、解答题（本大题共9题，共84分）

19．计算（共8分）

（1）；               （2）．

20．解方程：（共8分）

（1）；                （2）．

21．（本题满分8分）在□ABCD中，点E、F分别是AD、BC边上的点，且满足AE＝CF连接BE、DF．

（1）、求证：△ABE ≌ △CDF；

（2）、求证：四边形BEDF为平行四边行．

22．（本题满分8分）无锡某校为了开阔学生的视野，积极组织学生参加课外读书活动．“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如下两幅不完整的统计图（如图），请你结合图中的信息解答下列问题：

（1）求被调查的学生人数；

（2）求最喜爱艺体类图书的人数，并补全条形统计图；

（3）已知该校有1200名学生，估计全校最喜爱文学类图书的学生有多少人？

23．（本题满分10分）在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．

（1）点C的坐标是   ▲   ，△ABC的面积是   ▲   ；

（2）将△ABC绕点C旋转180°得到△A1B1C1，连接AB1、BA1，画出四边形AB1A1B，并判断四边形AB1A1B是何种特殊四边形   ▲   ；

（3）请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

24．（本题满分8分）烟台享有‘苹果之乡”的美誉．甲，乙两超市分别用3000元以相同的进价购进质量相同的苹果．甲超市销售方案是：将苹果按大小分类包装销售，其中大苹果400千克，以进价的2倍销售，剩下的小苹果以高于进价的10%销售．乙超市的销售方案是：不将苹果按大小分类，直接包装销售，价格按甲超市大，小两种苹果售价的平均数定价．若两超市将苹果全部售完，其中甲超市获利2100元（其它成本不计）．

问：（1）苹果进价为每千克多少元？

（2）乙超市获利多少元？并比较哪种销售方式更合算．

25．（本题满分10分）阅读下列材料：

方程的解为x＝1，

方程的解为x＝2，

方程的解为x＝3，

（1）请直接写出方程的解为   ▲   ；

（2）观察上述方程与解的特征，写出一个解为－5的分式方程：   ▲   ；

（3）观察上述方程与解的特征，写出能反映上述方程一般规律的方程，并直接写出这个方程的解：   ▲   ；   ▲   ．

26．（本题满分12分）已知，矩形中，，，的垂直平分线分别交、于点、，垂足为．

(1)如图1－1，连接、．求证四边形为菱形，并求的长；

(2)如图1－2，动点、分别从、两点同时出发，沿和各边匀速运动一周．即点自→→→停止，点自→→→停止．在运动过程中，

①已知点的速度为每秒5，点的速度为每秒4，运动时间为秒，当、、、四点为顶点的四边形是平行四边形时，求的值；

②若点P、Q的运动路程分别为a、b (单位：，ab≠0)，已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．

27．（本题满分12分）如图，矩形ABCD的边BC在x轴上，BC＝6，AB＝5，且3BO＝BC，若点E为x轴上一动点，连接DE，将△DCE沿直线DE翻折得到△DC’E．

（1）点D的坐标为   ▲   ；

（2）若点C’ 恰好落在y轴正半轴上时，则点E的坐标为   ▲    ；

（3）若E为射线CB上一点，当点C’ 恰好落在矩形对称轴上时，试求线段CE的长．

2021—2022学年第二学期八年级数学期中试卷参考答案

黑色矩形区域内答题，超出该区域的答案无效！