2021-2022学年重庆市育才中学教育集团八年级（下）期中数学试卷（无答案）

这是一份2021-2022学年重庆市育才中学教育集团八年级（下）期中数学试卷（无答案），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．以下列各组数为边长的三角形中，不能构成直角三角形的一组是（ ）
A．3、4、5B．4、5、6C．5、12、13D．6、8、10
2．函数y=中自变量x的取值范围是（ ）
A．x≤3B．x≠3C．x≠-3D．x≥3
3．甲、乙、丙、丁四名同学进行立定跳远测试，每人10次立定跳远成绩的平均数都是2.25米，方差分别是S甲2=0.72，S乙2=0.75，S丙2=0.68，S丁2=0.61，则这四名同学立定跳远成绩最稳定的是（ ）
A．甲B．乙C．丙D．丁
4．如图，在▱ABCD中，∠ABC的平分线交AD于E，∠BEA=30°，则∠A的大小为（ ）
A．100°B．120°C．130°D．150°
5．下列说法中正确的是（ ）
A．矩形的对角线平分每组对角
B．菱形的对角线相等且互相垂直
C．有一组邻边相等的矩形是正方形
D．对角线互相垂直的四边形是菱形
6．甲、乙两人沿同一条路从A地出发，去往100千米外的B地，甲、乙两人离A地的距离（千米）与时间t（小时）之间的关系如图所示，以下说法正确的是（ ）
A．甲出发2小时后两人第一次相遇
B．甲的速度是60km/h
C．乙的速度是30km/h
D．甲乙同时到达B地
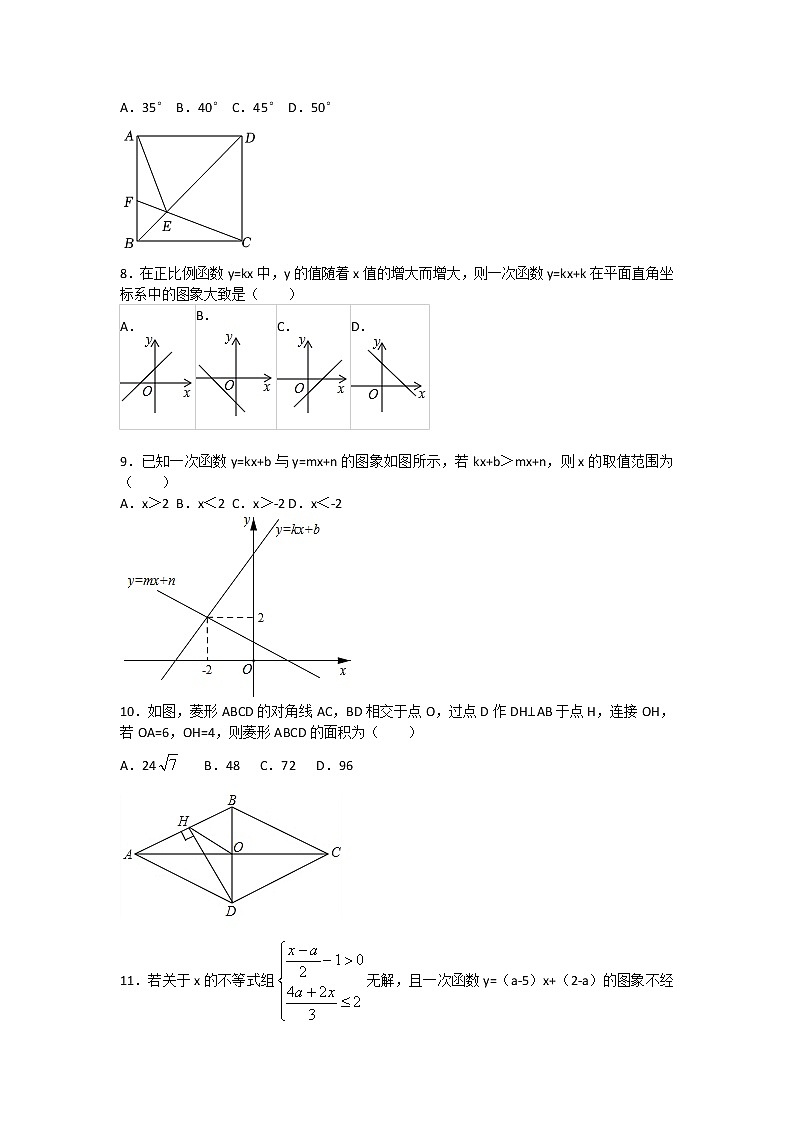
7．如图，正方形ABCD中，点F为AB上一点，CF与BD交于点E，连接AE，若∠BCF=20°，则∠AEF的度数（ ）
A．35°B．40°C．45°D．50°
8．在正比例函数y=kx中，y的值随着x值的增大而增大，则一次函数y=kx+k在平面直角坐标系中的图象大致是（ ）
9．已知一次函数y=kx+b与y=mx+n的图象如图所示，若kx+b＞mx+n，则x的取值范围为（ ）
A．x＞2B．x＜2C．x＞-2D．x＜-2
10．如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA=6，OH=4，则菱形ABCD的面积为（ ）
A．24B．48C．72D．96
11．若关于x的不等式组无解，且一次函数y=（a-5）x+（2-a）的图象不经过第一象限，则符合条件的所有整数a的和是（ ）
A．7B．8C．9D．10
12．下列说法正确的是（ ）
①若a2+b2+c2-2（a+b+c）+3=0，则a=b=c；
②a2+b2+c2=-2（ab+bc+ac），则a+b+c=0；
③若x2+xy+y=14，y2+xy+x=28，则x+y=6；
④实数x，y，z满足x2+y2+z2=4，则（2x-y）2+（2y-z）2+（2z-x）2的最大值是20．
A．①②B．①③④C．①②③D．①②③④
二、填空题：（本大题共4个小题，每小题4分，共16分）请将每小题的答案直接填在答题卷中对应的横线上。
13．关于x的方程（k-1）x|k|+1-x+5=0是一元二次方程，则k=______.
14．将直线y=-6x+2向下平移4个单位，平移后的直线解析式为_______.
15．如图，矩形ABCD的对角线AC的垂直平分线分别交AD、AC、BC于点E、O、F，若AB=6，BC=8，则EF的长为______.
16．如图，已知ABC为等边三角形，D、E分别为BC、AC上一点，并满足AE=CD，连接AD、BE相交于F点，连接CF，且CF⊥BF，过点B作BH⊥AD，与AC相交于G点，现将△ABF沿AB翻折得到OABF′，点I为BF中点，且AF=1，则点I到BF′的距离为____．
三、解答题：（本大题共8个小题，第17、18题，每小题8分，第19、20、21、22、23、24题，每小题8分，共76分）解答时每小题必须给出必要的演算过程或推理步骤．
17．计算：
（1）；
（2）．
18．解方程：
（1）x2-9=2x+6；
（2）3x2-6x+2=0．
19．如图，线段AD是△ABC的角平分线．
（1）尺规作图：作线段AD的垂直平分线分别交AB，AD，AC于点E，O，F；（保留痕迹，不写作法）
（2）在（1）所作的图中，连接DE，DF，求证：四边形AEDF是菱形．（请补全下面的证明过程）
证明：∵EF是线段AD的垂直平分线，
∴AE=____，AF=_____，
∵AD⊥EF，
∴∠AOE=∠AOF=90°，
∵线段AD是△ABC的角平分线，
∴∠BAD=_____，
∵∠AEF=90°-∠BAD，∠AFE=90°-∠CAD，
∴_______=∠AFE，
∴AE=______，
∴AE=AF=DF=DE，
∴四边形AEDF是菱形．
20．“粽子香，香厨房，艾叶香，香满堂．”端午节是传统佳节，为深入了解我国传统节日．现从七、八两个年级各随机抽取20名学生进行了相关知识测试，获得了他们的成绩m （百分制，单位：分），并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息．
七年级20名学生成绩如下：
50，59，62，66，66，66，66，71，72，73，73，80，81，82，82，83，83，84，91，92．
八年级20名学生成绩的扇形统计图（如图）
七、八年级学生成绩统计表
其中，八年级20名学生成绩中分数在80≤m＜90之内包含的所有数据如下：
80，80，84，86，87，87，88．
请根据所给信息，解答下列问题：
（1）a=_____；b=______；c=_____．
（2）若八年级有1000名学生参加此次测试，成绩80分及以上为优秀，请估计八年级成绩优秀的学生人数；
（3）在此次测试中，你认为哪个年级成绩更好？请说明理由．
21．如图，在平面直角坐标系中，作出函数y=x+2的图象，（请先填表再作图，不写作法，不下结论）
列表：
（1）m=____；n=_____．
（2）若直线y=x+2与直线y=3x交于点A，点B在直线y=x+2上且横坐标为-4，连接OB，求△OAB的面积．
22．如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD，AD交BE于点O．
（1）求证：AD与BE互相平分；
（2）若AB⊥AC，AC=BF，BE=8，FC=2，求AB的长．
23．某校需要购进一批消毒液，经了解，某商场供应A、B两种类型的消毒液．购买2瓶A类型消毒液所需费用和3瓶B类型消毒液所需费用相同；购买3瓶A类型消毒液和1瓶B类型消毒液共需要55元．
（1）求A，B两种类型消毒液的单价．
（2）若根据需求，需要购买A，B两种类型消毒液共300瓶，其中A类型消毒液的数量不少于B类型消毒液数量的，当A类型消毒液购买多少瓶时能使得总花费最少，最少的总花费为多少元？
24．在平面直角坐标系中，直线l经过点A （2，0）和点B（0，2）．点C的横坐标为，点D为线段OB的中点．
（1）求直线l的解析式；
（2）如图1，若点P为线段OA上的一个动点，当PC+PD的值最小时，求出点P坐标；
（3）在（2）的条件下，点Q在线段AB上，若△DPQ是等腰三角形，请直接写出满足条件的点Q的横坐标，并写出其中一个点Q的横坐标的求解过程．
四、解答题：（本大题共1个小题，共10分）解答时每小题必须给出必要的演算过程或推理步骤。
25．已知△ABC为等边三角形，边长为4，点D、E分别是BC、AC边上一点，连接AD、BE，且AE=CD．
（1）如图1，若AE=2，求BE的长度；
（2）如图2，点F为AD延长线上一点，连接BF、CF，AD、BE相交于点G，连接CG，已知∠EBF=60°，CE=CG，求证：BF+GE=2CF；
（3）如图3，点P是△ABC内部一动点，顺次连接PA、PB、PC，请直接写出PA+PB+2PC的最小值．

A．
B．
C．
D．
年级
平均分
中位数
众数
分数70≤m＜80所占百分比
七年级
74.1
73
b
20%
八年级
77.9
a
78
c
x
0
n
y=x+2
m
0